摘要:總結股票均線計算原理--線性關係,也是以後大數據處理的基礎之一,NumPy的 linalg 包是專門用於線性代數計算的。作一個假設,就是一個價格可以根據N個之前的價格利用線性模型計算得出。 前一篇,在計算均線,指數均線時,分別計算了不同的權重,比如 和 都是按不同的計算方法來計算出相關的權重, ...
摘要:總結股票均線計算原理--線性關係,也是以後大數據處理的基礎之一,NumPy的 linalg 包是專門用於線性代數計算的。作一個假設,就是一個價格可以根據N個之前的價格利用線性模型計算得出。
前一篇,在計算均線,指數均線時,分別計算了不同的權重,比如

和
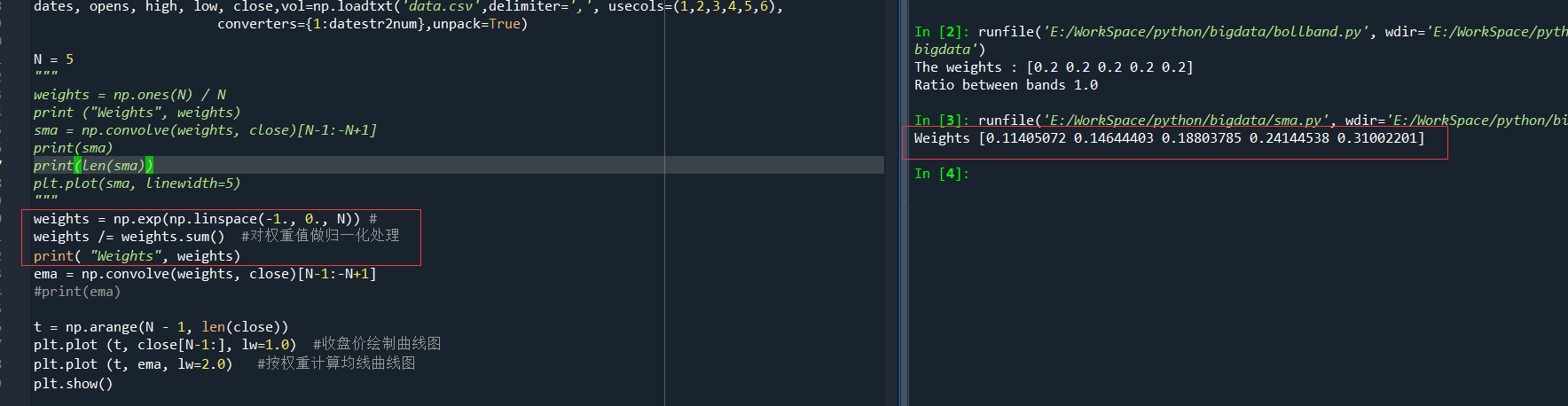
都是按不同的計算方法來計算出相關的權重,一個股價可以用之前股價的線性組合表示出來,也即,這個股價等於之前的股價與各自的繫數相乘後再做加和的結果,但是,這些繫數是需要我們來確定的,也即一個線性相關的權重。
一、用線性模型預測價格
創建步驟如下:
1)先獲取一個包含N個收盤價的向量(數組):
N=10 #N=len(close) new_close = close[-N:] new_closes= new_close[::-1] print (new_closes)
運行結果:[39.96 38.03 38.5 38.6 36.89 37.15 36.61 37.21 36.98 36.47]
2)初始化一個N×N的二維數組 A ,元素全部為 0
A = np.zeros((N, N), float) print ("Zeros N by N", A)
3)用數組new_closes的股價填充數組A
for i in range(N): A[i,] = close[-N-i-1: -1-i] print( "A", A)
試一下運行結果,並觀察填充後的數組A
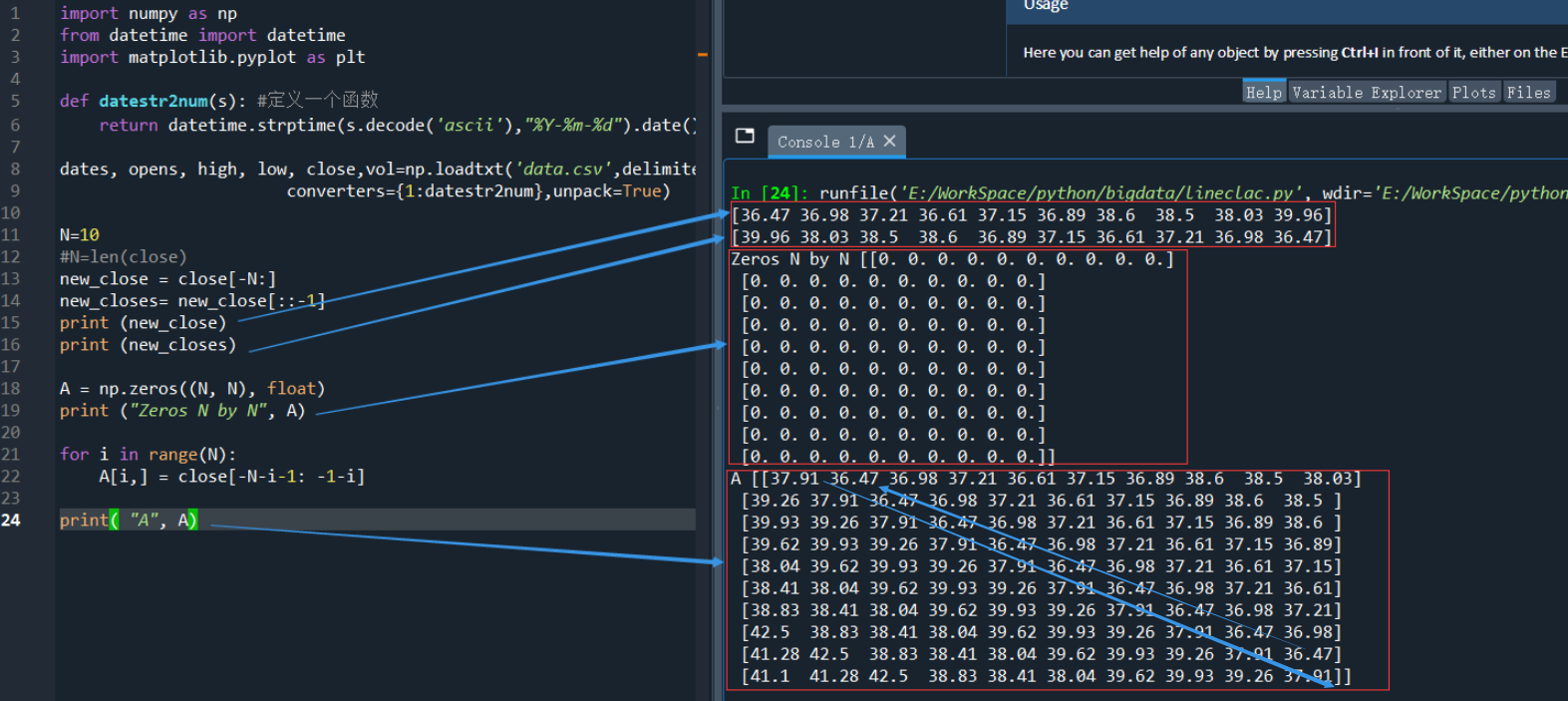
4)選取合適的權重
Weights [0.11405072 0.14644403 0.18803785 0.24144538 0.31002201]和The weights : [0.2 0.2 0.2 0.2 0.2]哪一種權重更合理?用線性代數的術語來說,就是解一個最小二乘法的問題。
要確定線性模型中的權重繫數,就是解決最小平方和的問題,可以使用 linalg包中的 lstsq 函數來完成這個任務
(x, residuals, rank, s) = np.linalg.lstsq(A,new_closes)
其中,x是由A,new_closes通過np.linalg.lstsq()函數,即生成的權重(向量),residuals為殘差數組、rank為A的秩、s為A的奇異值。
5)預測股價,用NumPy中的 dot()函數計算繫數向量與最近N個價格構成的向量的點積(dot product),這個點積就是向量new_closes中價格的線性組合,繫數由向量 x 提供
print( np.dot(new_closes, x))
完整代碼如下:
import numpy as np from datetime import datetime import matplotlib.pyplot as plt def datestr2num(s): #定義一個函數 return datetime.strptime(s.decode('ascii'),"%Y-%m-%d").date().weekday() dates, opens, high, low, close,vol=np.loadtxt('data.csv',delimiter=',', usecols=(1,2,3,4,5,6), converters={1:datestr2num},unpack=True) N=10 #N=len(close) new_close = close[-N:] new_closes= new_close[::-1] A = np.zeros((N, N), float) for i in range(N): A[i,] = close[-N-i-1: -1-i] print( "A", A) (x, residuals, rank, s) = np.linalg.lstsq(A,new_closes) print(x) #權重繫數向量 print('\n') print(residuals) #殘差數組 print('\n') print(rank) #A的秩 print(s) print('\n')#奇異值 print( np.dot(new_closes, x))
運行結果如下: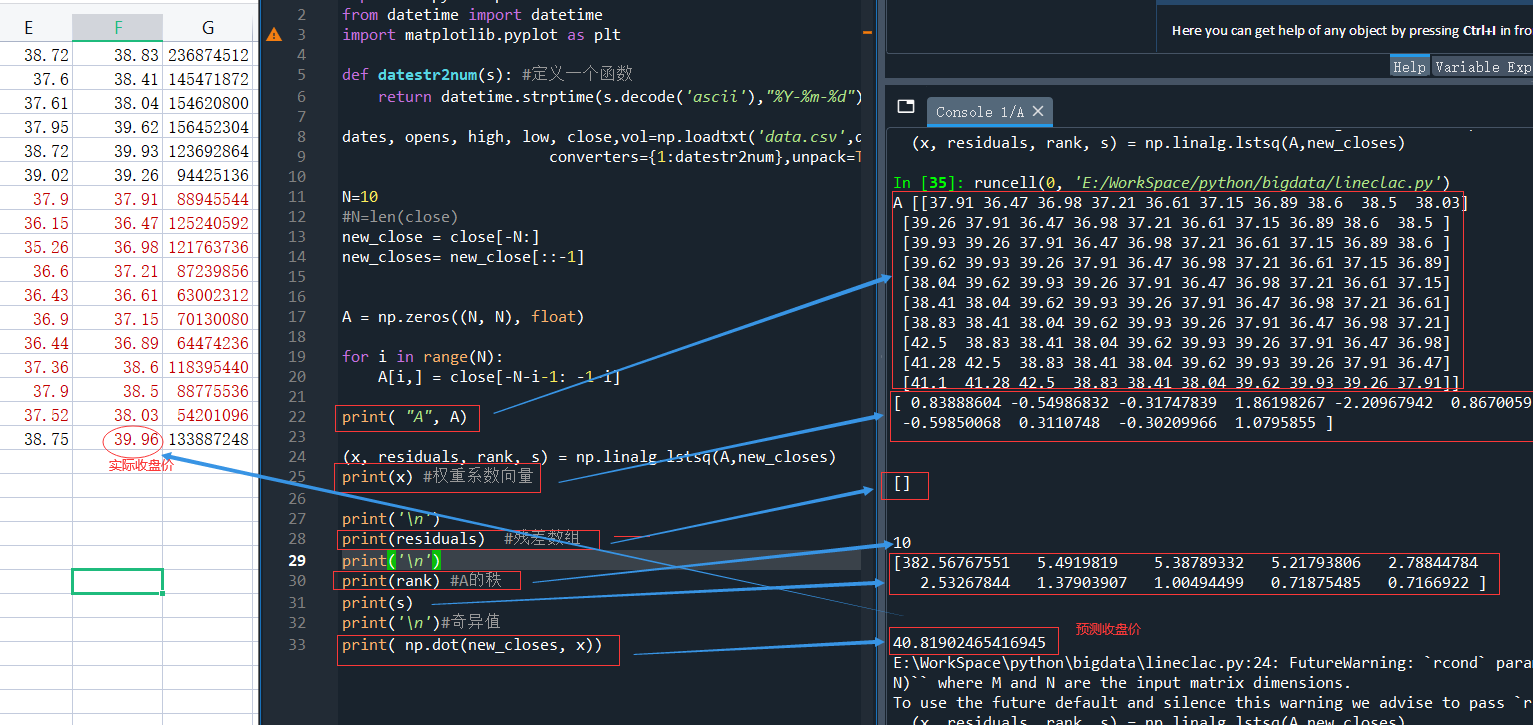
二、趨勢線
趨勢線,是根據股價走勢圖上很多所謂的樞軸點繪成的曲線。描繪價格變化的趨勢。可以讓電腦來用非常簡易的方法來繪製趨勢線
(1) 確定樞軸點的位置。假定樞軸點位置 為最高價、最低價和收盤價的算術平均值。pivots = (high + low + close ) / 3
從樞軸點出發,可以推導出股價所謂的阻力位和支撐位。阻力位是指股價上升時遇到阻力,在轉跌前的最高價格;支撐位是指股價下跌時遇到支撐,在反彈前的最低價格(阻力位和支撐位並非客觀存在,它們只是一個估計量)。基於這些估計量,就可以繪製出阻力位和支撐位的趨勢線。我們定義當日股價區間為最高價與最低價之差
(2) 定義一個函數用直線 y= at + b 來擬合數據,該函數應返回繫數 a 和 b,再次用到 linalg 包中的 lstsq 函數。將直線方程重寫為 y = Ax 的形式,其中 A = [t 1] , x = [a b] 。使用 ones_like 和 vstack 函數來構造數組 A
numpy.ones_like(a, dtype=None, order='K', subok=True) 返回與指定數組具有相同形狀和數據類型的數組,並且數組中的值都為1。
numpy.vstack(tup) [source] 垂直(行)按順序堆疊數組。 這等效於形狀(N,)的1-D數組已重塑為(1,N)後沿第一軸進行concatenation。 重建除以vsplit的數組。如下兩小例:
>>> a = np.array([1, 2, 3])
>>> b = np.array([2, 3, 4])
>>> np.vstack((a,b))
array([[1, 2, 3],
[2, 3, 4]])
>>> a = np.array([[1], [2], [3]])
>>> b = np.array([[2], [3], [4]])
>>> np.vstack((a,b))
array([[1],
[2],
[3],
[2],
[3],
[4]])
完整代碼如下:
import numpy as np from datetime import datetime import matplotlib.pyplot as plt def datestr2num(s): #定義一個函數 return datetime.strptime(s.decode('ascii'),"%Y-%m-%d").date().weekday() dates, opens, high, low, close,vol=np.loadtxt('data.csv',delimiter=',', usecols=(1,2,3,4,5,6), converters={1:datestr2num},unpack=True) """ N=10 #N=len(close) new_close = close[-N:] new_closes= new_close[::-1] A = np.zeros((N, N), float) for i in range(N): A[i,] = close[-N-i-1: -1-i] print( "A", A) (x, residuals, rank, s) = np.linalg.lstsq(A,new_closes) print(x) #權重繫數向量 print(residuals) #殘差數組 print(rank) #A的秩 print(s) print( np.dot(new_closes, x)) """ pivots = (high + low + close ) / 3 def fit_line(t, y): A = np.vstack([t, np.ones_like(t)]).T # np.ones_like(t) 即定義一個像t一樣,有相同形狀和數據類型的數組,並且數組中的值都為1 return np.linalg.lstsq(A, y)[0] t = np.arange(len( close)) #按close數列創建一個數列t sa, sb = fit_line(t, pivots - (high - low)) #用直線y=at+b來擬合數據,該函數應返回繫數a(sa) 和 b(sb) ra, rb = fit_line(t, pivots + (high - low)) support = sa * t + sb #計算支撐線數列 resistance = ra * t + rb #計算阻力線數列 condition = (close > support) & (close < resistance)#設置一個判斷數據點是否位於趨勢線之間的條件,作為 where 函數的參數 between_bands = np.where(condition) plt.plot(t, close,color='r') plt.plot(t, support,color='g') plt.plot(t, resistance,color='y') plt.show()
運行結果:

三、數組的修剪和壓縮
NumPy中的 ndarray 類定義了許多方法,可以對象上直接調用。通常情況下,這些方法會返回一個數組。
ndarray 對象的方法相當多,像前面遇到的 var 、 sum 、 std 、 argmax 、argmin 以及 mean 函數也均為 ndarray 方法。下麵介紹一下數組的修前與壓縮。
1、 clip 方法返回一個修剪過的數組:將所有比給定最大值還大的元素全部設為給定的最大值,而所有比給定最小值還小的元素全部設為給定的最小值
a = np.arange(10) print("a =", a) print("Clipped", a.clip(3, 7))
運行結果:
a = [0 1 2 3 4 5 6 7 8 9]
Clipped [3 3 3 3 4 5 6 7 7 7]
很明顯,a.clip(3,7)將數組a中的小於3的設置為3,大於7的全部設置為7.
2、 compress 方法返回一個根據給定條件篩選後的數組
b = np.arange(10) print (a) print ("Compressed", a.compress(a >3))
運行結果:
[0 1 2 3 4 5 6 7 8 9]
Compressed [4 5 6 7 8 9]
四、階乘
prod() 方法,可以計算數組中所有元素的乘積.
c = np.arange(1,5) print("b =", c) print("Factorial", c.prod())
運行結果:
b = [1 2 3 4]
Factorial 24
如果想知道1~8的所有階乘值,調用 cumprod()方法,計算數組元素的累積乘積。
print( "Factorials", c.cumprod())
運行結果:
Factorials [ 1 2 6 24 120]

本篇主要介紹了一個通過現在有數據,用函數 y= at + b 來擬合數據進行線性擬合後,用 linalg包中的 lstsq 函數來完成最小二乘相關後,預測股價的實例,來瞭解了一些numpy的函數及作用;同時介紹 了數據修剪及壓縮和階乘的計算。



