拓撲排序 簡介 拓撲排序是將偏序的數據線性化的一種排序方法。複習下偏序和全序的概念: 全序關係是偏序關係的一個子集。 全序是集合內任何一對元素都是可比較的,比如數軸上的點都具有一個線性的數值,因此根據數值就可以進行比較。 偏序是集合內不是所有元素都是可以比較的,比如平面內的點由橫坐標和縱坐標組成,是 ...
拓撲排序
簡介
拓撲排序是將偏序的數據線性化的一種排序方法。複習下偏序和全序的概念:
全序關係是偏序關係的一個子集。
全序是集合內任何一對元素都是可比較的,比如數軸上的點都具有一個線性的數值,因此根據數值就可以進行比較。
偏序是集合內不是所有元素都是可以比較的,比如平面內的點由橫坐標和縱坐標組成,是不可直接比較大小的。這是因為橫坐標和縱坐標是兩個維度,在每個維度內都可以用數值比較,但是維度之間不可量化比較(就像學習成績和身體素質之間無法量化比較)。當然偏序是個數學概念,未必是多維度引發的不可比較,只需滿足以下關係即滿足偏序關係:
設 P 是集合,P 上的二元關係“≤”滿足以下三個條件,則稱“≤”是 P 上的偏序關係(或部分序關係):
(1)自反性:a≤a,∀a∈P;
(2) 反對稱性:∀a,b∈P,若 a≤b 且b≤a,則 a=b;
(3) 傳遞性:∀a,b,c∈P,若 a≤b 且b≤c,則 a≤c;
註意這裡的“≤”是一個自定義的二元運算符,而不是通常的線性運算的大小關係。
理解了偏序關係之後,拓撲排序就是將偏序關係線性化。舉一個具體場景,在有向無環圖中,“節點 A 是否可由節點 B 到達”即是一種偏序關係。在該有向無環圖中節點,在不移動的情況下可以到達自身,因此滿足自反性。且在有向無環圖中不存在環,若 A 可到達 B 且 B可到達A,則A,B 必是相同節點,因此滿足反對稱性。當節點 A 可以到達節點 B,且節點 B 可以到達節點C 時,節點 A 也可以到達節點 C,因此滿足傳遞性。
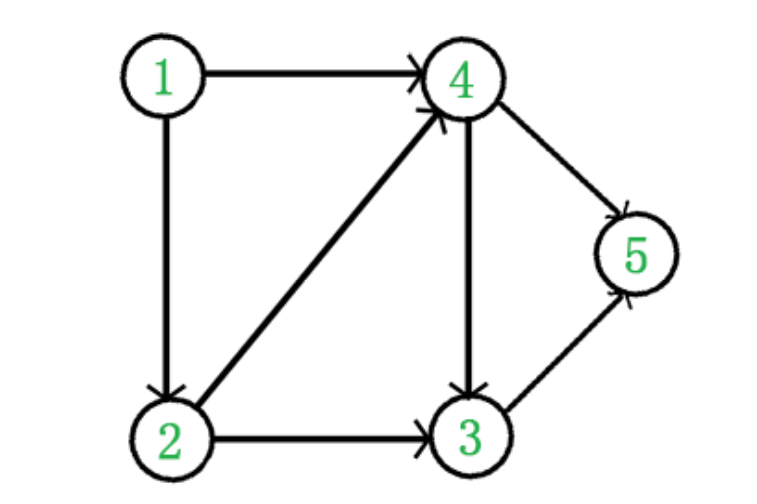
在該場景下,拓撲排序即是將有向無環圖中所有節點按照“節點 A 是否可由節點 B 到達”來進行線性化排序。如上圖所示,對它進行拓撲排序可以使用深度優先演算法完成,深度優先演算法可以複習課件,其過程大概如下。
- 選取頂點 s(一般選取入度比較小的節點更合適,比如上圖的節點 1),標記狀態
- 若 s 有未被訪問的鄰居,則選擇鄰居標記狀態繼續訪問,否則返回
- 如果一次深度優先搜索還有節點未被訪問,則重覆步驟 1,直到所有節點被訪問到
這種方法可以將滿足偏序關係的有向無環圖線性化為


