枚舉 對於一些簡單的題目,我們或許不需要用什麼太巧妙的方法,只需要把所有的可能性列舉出來,然後逐一試驗就可以了。 總的來說,枚舉就是通過列舉所有的可能性進行一一判斷檢查。 方法 通過事先把各種可能發生的事情都列舉一遍,為後面求解提供結果。 總的來說,兩種方法: 遞歸枚舉,這種方法往往更直觀; 遞推( ...
枚舉
對於一些簡單的題目,我們或許不需要用什麼太巧妙的方法,只需要把所有的可能性列舉出來,然後逐一試驗就可以了。
總的來說,枚舉就是通過列舉所有的可能性進行一一判斷檢查。
方法
通過事先把各種可能發生的事情都列舉一遍,為後面求解提供結果。
總的來說,兩種方法:
遞歸枚舉,這種方法往往更直觀;
遞推(迴圈)枚舉,這種方法往往寫起來更簡潔。
常見類型
枚舉排列
枚舉子集
優化
在某些情況下,直接枚舉可能會帶來較差的效果,在這種時候,我們實際上可以分析題目,根據題目的一些性質或特點去除大部分的列舉,減小枚舉量,從而提高枚舉的效率。
搜索
搜索,某種意義上就是對於枚舉演算法的一種改進,通過在枚舉的過程中,不斷排除一些不可能達到的情況,從而達到優化複雜度的效果。
深度優先搜索(DFS)
深度優先搜索的思想就是:從一個頂點沿一條路一直走,如果發現到不了目標節點,則返回上一個節點,沿另一條路一直走到底。
總的來說,DFS就是一個一個處理到底,發現無法得到結果之後,逐步返回尋求其它的出路。
DFS的應用並不局限於一般的圖上,其往往用於一些狀態圖上。
剪枝
指通過過程當中的一些量確定不可行或不符合最優的情況。
寬度優先搜索(BFS)
寬度優先搜索的核心思想在於:首先訪問起始節點的所有鄰接點,然後再訪問較遠的區域,逐步擴大範圍,直到找到目標節點。
BFS也主要運用於處理狀態圖,尤其在一些尋求最優方案的題目中有較大的用處。
BFS處理不含邊權的圖的求解最短路徑問題非常有效。
兩種方法的優缺點
深度優先搜索,優點在於能較高效地逼近解,缺點在於初始遞歸方向錯誤會帶來很嚴重後果;
寬度優先搜索,優點在於能迅速找到答案不算大的解,缺點在於解答案較大時所耗時間與空間都比較大。
迭代加深搜索
在綜合以上兩種演算法之後,出現了一個折中的方法:
通過限定下界k,然後先深度優先搜索k層,如果仍沒有找到有效解,則增大下界。
這個方法的優點在於:相對於深度優先搜索並沒有大很多的時間開銷,但能部分解決深度優先搜索的局限,沒有寬度優先搜索一般的大空間需求。
分治
分治演算法的基本思想:將一個較大規模的問題分成多個(一般是2個)較小規模的互相獨立且與原問題相同的子問題,那麼只需要通過對子問題的求解,就可以得到原問題的解。
往往子問題會採取相同的方法繼續分治下去,因此分治演算法一般會採取遞歸的方式表現。
步驟
分解:將要解決的問題劃分成若幹規模較小的同類問題;
求解:當子問題劃分得足夠小時,用較簡單的方法解決;
合併:按原問題的要求,將子問題的解逐層合併構成原問題的解。
應用
二分查找
歸併排序
快速冪
貪心
貪心演算法指的是在對問題求解過程中,總是做出目前來看最優的選擇,也就是說貪心演算法不會考慮全局最優解,只會不斷考慮局部最優解。
但是,我們需要註意到,局部最優解不一定就是全局最優解。
貪心演算法往往可以以較低的代碼複雜度與時間複雜度而得到較優的結果,對於求解近似值的作用很大。
而對於相當一部分需要求解最優值的問題,我們會發現通常可以採用動態規劃或者網路流的方法取代貪心演算法。
考試技巧
STL
STL 是“Standard Template Library”的縮寫,中文譯為“標準模板庫”。
#include<algorithm>
#include<bits/stdc++.h>(推薦)
sort()
sort函數用於給一個數組進行排序,在algorithm庫里。
使用方法為sort(v.begin(),v.end(),cmp)),這裡的v.begin()是開始的指針位置,v.end()是結束的指針位置(這裡的表示是左閉右開,也就是說v.end()並不在排序內容里),cmp可要可不要,如果使用的是自定義類型且沒有重載運算符就一定需要。
這個數組的類型可以是自定義類型或者STL中的vector,需要註意的是如果採用的是自定義類型則需要重載運算符(也可以如上面說的一樣用cmp)。
stack
模擬棧,在<stack>里。
stack <Type> A;
常用函數
A.push(a);
入棧
A.pop();
出棧
A.top();
返回棧頂元素(但不出棧)
queue
模擬隊列,在<queue>里。
queue <Type> A;
常用函數
A.push(a);
入隊
A.pop();
出隊
A.front();
返回隊首元素(但不出隊)
deque
雙端隊列
priority queue
優先隊列,一個類似於堆的數據結構,在<queue>里。
預設是大根堆,如果想讓他是小根堆的話有兩種辦法,其中一種是重載小於號。
能以O(logN)複雜度完成插入元素,刪除最值,尋找最值。
Priority_queue <Type> A;
常用函數
A.push(a);
插入
A.pop();
刪除最值(預設為最大值)
A.top();
返回最值(但不刪除)

pair
一個包含兩個可以不同的數據值的類型。
pair <Type1,Type2> A;
往往Type1,Type2都是標準類型,但如果是自定義類型,需要重定義運算符;
常用函數
賦值:make_pair(t1,t2);
返回對應的值:A.first,A.second;
vector
向量(Vector)是一個封裝了動態大小數組的順序容器。跟任意其它類型容器一樣,它能夠存放各種類型的對象。可以簡單的認為,向量是一個能夠存放任意類型的不定長的動態數組,在vector庫里。
定義方式:vector <Type> A;
容器特性
順序序列
順序容器中的元素按照嚴格的線性順序排序。可以通過元素在序列中的位置訪問對應的元素。
動態數組
支持對序列中的任意元素進行快速直接訪問,甚至可以通過指針算述進行該操作。提供了在序列末尾相對快速地添加/刪除元素的操作。
能夠感知記憶體分配器的(Allocator-aware)
容器使用一個記憶體分配器對象來動態地處理它的存儲需求。
相當於是個動態數組,每次可以往末端插入一個元素,下標從0開始。
實現方式是每次不夠大的時候暴力倍長,可以發現均攤是線性的。
常用操作
A.clear();
清空
A.push_back(a);
尾部添加元素
A.pop_back();
尾部刪除元素
A.empty();
檢查是否為空,空返回true
v.size()
這個一個unsigned int類型。也就是說對空的vector的size()-1會得到2^32-1。因此寫代碼的時候應帶儘量避免這種寫法。(或者強制類型轉化成int)
v.resize()
其複雜度是O(max(1, resize()中的參數-原來的size()))的。
如果是大小變大的resize(),且可以指定新擴展的位置的值。若未指定則調用其預設構造函數,例如int之類的會預設是0。
v.clear()和vector<int>().swap(v)的區別。
前者是假裝清空了,實際記憶體沒有被回收。
後者是真的回收了,不過需要和v.size()的大小成正比的時間。
後者的意思是使用vector<>()這句話調用無參的構造函數生成一個vector<>類型的對象,然後和v交換,之後其生存期結束被銷毀會自動調用其~vector<>()析構函數。註意<>裡面要寫v一樣的類型(例如int)

set
一個存儲集合的容器,在set庫里。
map相當於是一個下標可以是任何數值的數組,如果訪問時沒有賦值就會返回零。
內部使用紅黑樹(一種平衡樹)實現。
當set<>中的第一個參數是自定義類型的時候需要重新定義小於號。
複雜度基本上是O(log(當前大小))。
定義方式:set <Type> A;
常用函數
A.insert(a);
插入a
A.erase(a);
刪除a:
A.find(a);
查找a,如果查找成功,返回對應指針,查找失敗返回尾指針
A.begin(),A.end();
返回頭指針與尾指針,尾指針不存儲具體內容

map
存儲一個從key到value的映射。某種意義上就是“廣義”數組,在map庫里。
map相當於是一個下標可以是任何數值的數組,如果訪問時沒有賦值就會返回零。
內部使用紅黑樹(一種平衡樹)實現。
當map<,>中的第一個參數是自定義類型的時候需要重新定義小於號。
複雜度基本上是O(log(當前大小))
map <Type1,Type2> A;Type1是key類型,Type2是value類型。
可以通過A[B]=C這種形式賦值,B為Type1,C為Type2。
常用函數
A.clear();
清空
A.empty();
判斷是否為空
A.insert(pair<Type1,Type2> (C,D));
插入(不建議這麼寫)
A.erase(B);
刪除,B可以是key值也可以是指針
A.begin(),A.end();
頭指針,尾指針
m[x]
哪怕你什麼也不幹只寫一個m[x];也會新建一個點。
因此當你想知道map中是否存在這個映射的時候最好使用m.count(x)。
很多時候可以有效卡常。

multiset和multimap
是可重集合和可重映射。
有兩個註意的:第一個是count函數複雜度變成了O(lg(集合大小)+答案)的,也就是如果有很多相同元素,那麼count函數代價很大。
第二個是刪除x的話,使用s.erase(x)會把所有權值為x的刪除。
如果只想刪掉一個需要s.erase(s.find(x))。
unordered_set和unordered_map
基於哈希實現的集合和映射。
基本上裡面的類型只能是int,long long,double這種非自定義類型。 因為其基於哈希)
在c++11及以後存在,之前沒有,亂用可能會CE。
空間常數比較大,時間常數不小,比數組訪問慢很多,慎用。
不能順序遍歷,不支持lower_bound。
迭代器
只介紹set/map的迭代器。

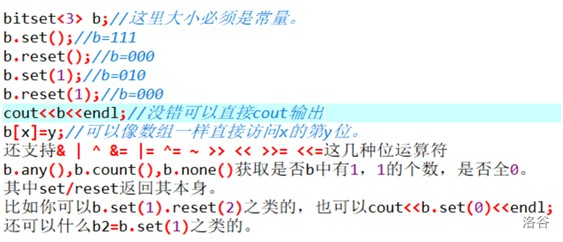
bitset
高精度壓位二進位。
一個用於處理二進位串的“數組”,在<bitset>里。
所有時間複雜度是線性的操作,常數都是1/32大概。
下標從0開始。
bitset <n> A;//n為長度;
支持所有位運算: << , >> , & , | , ^ ;
常用函數
A.count();
統計1的個數
A.reset();
清0
A.set();
全賦為1
A.size();
返回位數
lower bound()/upper bound()
lower_bound(v.begin(),v.end(),c)可以在一個有序數組當中找出剛好大於或等於c的數,在algorithm庫里,可以使用自定義類型,用法與sort相類似。
upper_bound函數類似,這個函數則是在有序數組中找出剛好大於c的數。
next permutation/prev permutation(全排列演算法)
algorithm頭文件中包含了next_permutation(v.begin(),v.end())和prev_permutation(v.begin(),v.end())兩個全排列函數,分別給出一個序列在全排列中的下一個和上一個序列(按字典序),如果存在這樣的序列則返回true,不存在則返回false,但仍會得到一個序列。
對於一個任意元素不相同的序列來說,正序排列是最小的排列方式,相應的逆序排列是最大的排列方式,以整數序列{1,2,3}為例,{1,2,3}是第一個排列,{3,2,1}則是最後一個排列,因此序列{1,2,3}沒有上一個序列,{3,2,1}沒有下一個序列。
pq.swap(pq2)
優先打暴力
考試中經常會遇到想到正確解法卻由於寫錯導致分數掛零的現象,為了應付這種情況,我們可以優先寫暴力程式,一來做分數保障,二來可以為對拍做準備。
多貪心原則
當一些題目的正解想不出來,並且一個貪心原則效果不好的情況下,可以採取多個貪心原則同時用,然後取最優的方案。(時間問題一般不用貪心,因為貪心演算法時間複雜度往往比較小)
特判
有些時候在想不到正解的情況下,可以通過判斷一些特殊情況得到部分分;有些情況雖然想到了正解,卻忽略了一些特殊情況,也無法得全分。
打表
有一些題目,看上去非常複雜,但是我們實際上可以通過打表看出規律或者可能性不多,可以直接通過打表得到答案。
補充
基本位運算
位與(&)
給定兩個長度相同的二進位串A、B(不同則在前面補0),A與B的結果的每一位由A與B的對應位決定,如果A與B的對應位均為1,則結果的那一位為1,否則為0。
位或(|)
A或B的結果的每一位同樣由A與B的對應位決定,如果A或B的對應位為1,則結果的那一位為1,否則為0。
位異或(xor)
A異或B的結果的每一位同樣由A與B的對應位決定,如果A與B的對應位不相同,則結果的那一位為1,否則為0。
左移(<<)
a<<b,左移,b以10進位表示。表示將a的最右邊(最低位)加上b個0。(相當於乘上了2ⁿ)。
右移(>>)
a>>b,右移,b以10進位表示。表示將a最右面(最低位)的b位刪掉。(相當於整除2ⁿ)。
並非原創,僅是整理,請見諒
Lo問我為什麼看星星。我覺得銀河和代碼是同一種東西,這也是一種回答。————Co


