前端程式員學好演算法系列（十）動態規劃

動態規劃整體思路是用遞歸問題求解，然後對遞歸過程中存在的大量重疊子問題進行優化，自頂向下的求解的思路為記憶化搜索，自底向上的解決問題的思想就是動態規劃，自頂向下的求解通常更好理解，我們理解後在改成自底向上的動態規劃求解；劍指 Offer 10- I. 斐波那契數列寫一個函數，輸入 n ，求斐波那 ...

動態規劃整體思路是用遞歸問題求解，然後對遞歸過程中存在的大量重疊子問題進行優化，自頂向下的求解的思路為記憶化搜索，自底向上的解決問題的思想就是動態規劃，自頂向下的求解通常更好理解，我們理解後在改成自底向上的動態規劃求解；

劍指 Offer 10- I. 斐波那契數列
寫一個函數，輸入 n ，求斐波那契（Fibonacci）數列的第 n 項。斐波那契數列的定義如下：

F(0) = 0, F(1) = 1
F(N) = F(N - 1) + F(N - 2), 其中 N > 1.
斐波那契數列由 0 和 1 開始，之後的斐波那契數就是由之前的兩數相加而得出。

答案需要取模 1e9+7（1000000007），如計算初始結果為：1000000008，請返回 1。

示例 1：

輸入：n = 2
輸出：1

示例 2：

輸入：n = 5
輸出：5

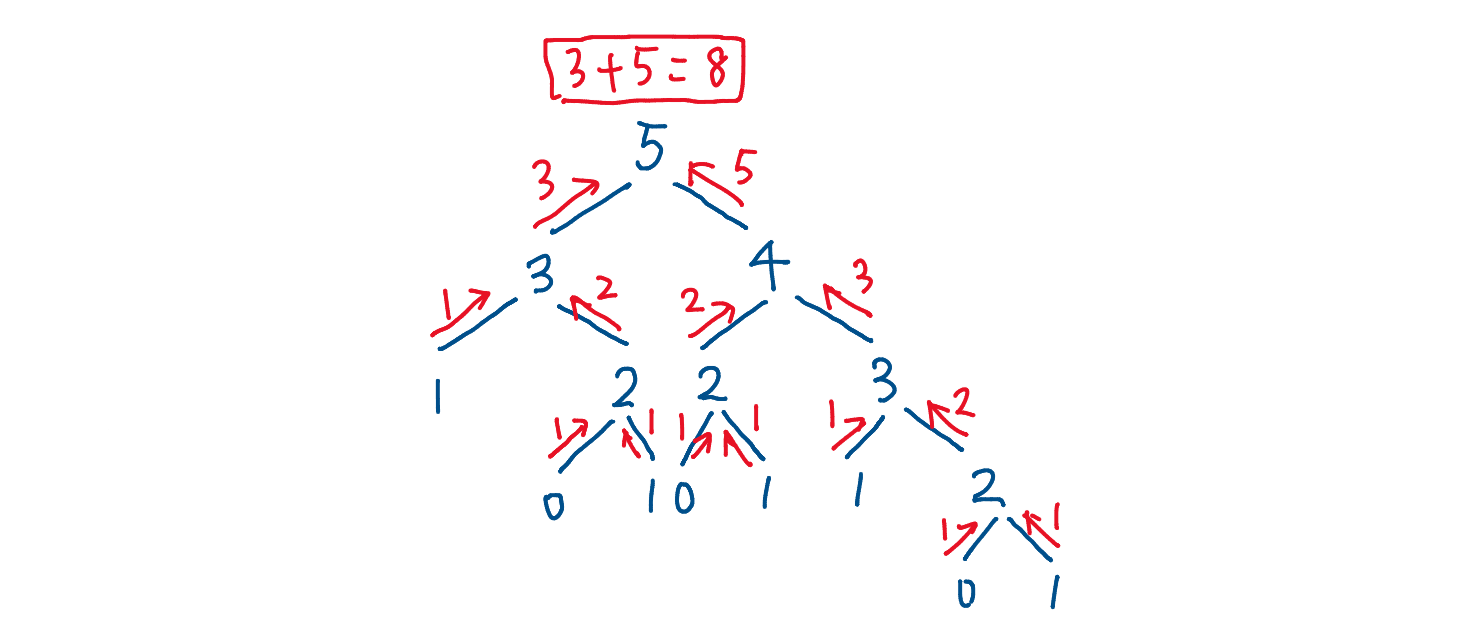
1.斐波那契的思想，就是我們求fib(n) 的解轉化為我們求 fib(n-1)+fib(n-2) ,fib(n-1) 我們可以轉化為 fib(n-1-1) + fib(n-2-1) ，隨著遞歸進行，我們最後會得到n=1和 n=0的時候，同時我們知道 n=0時fib(0) 等於0 fib(1)等於1，

/**
 * @param {number} n
 * @return {number}
 */
var fib = function(n) {
    if(n==0){
      return 0 
    }
    if(n==1){
       return 1
    }
    return fib(n-1) +fib(n-2)
};

2，上述代碼實現了一個斐波那契數列，但是對於斐波那契數列數列的時間複雜度是o的n次方的，因為我們求解的時候存在大量的重覆求解，在上面的基礎上運用cache 緩存計算結果 cache[n] 存在時直接求解，防止重覆計算，

/**
 * @param {number} n
 * @return {number}
 */
var fib = function(n) { 
    const cache = {
        0:0n,
        1:1n,
    };
    return Fibonacci(n) % 1000000007n;
    function Fibonacci(n){
        if(cache[n]!==undefined) {
            return cache[n]
        }
        cache[n] = Fibonacci(n - 1) + Fibonacci(n - 2)
        return cache[n];
    }
    
};

3.我們改造成動態規劃的求解方式，自下向上的解決問題，fibonacci = 0 時 fib(0) 為0 fibonacci 為1時fib(1) =1 fibonacci[2] = fibonacci[2-1] + fibonacci[2-2] ，我們求n的解只需求解 fibonacci[n]

/**
 * @param {number} n
 * @return {number}
 */
var fib = function(n) {
    let fibonacci = [0,1];
    for(let i = 2; i <= n; i ++) {
        fibonacci[i] = (fibonacci[i - 1] + fibonacci[i - 2]) % (1e9 +7);
    }
    return fibonacci[n];

};

我們再看一個典型的斐波那契問題

70. 爬樓梯
假設你正在爬樓梯。需要 n 階你才能到達樓頂。

每次你可以爬 1 或 2 個臺階。你有多少種不同的方法可以爬到樓頂呢？

註意：給定 n 是一個正整數。

示例 1：

輸入： 2
輸出： 2
解釋： 有兩種方法可以爬到樓頂。
1. 1 階 + 1 階
2. 2 階

解題：該題和上題思路相同，我們就不深入講解了，我們使用記憶結果時可以使用對象，也可以使用數組
1.自頂向下求解

/**
 * @param {number} n
 * @return {number}
 */
var climbStairs = function (n,map={1:1,2:2}) {
    if (map[n]) return map[n];
    else map[n]=map[n-1]+map[n-2];
    return climbStairs(n - 1,map) + climbStairs(n - 2,map);
};

2. 自底向上求解

/**
 * @param {number} n
 * @return {number}
 */
var climbStairs = function (n) {
      let catche = [1,1]
      for(let i=2;i<=n;i++){
         catche[i] = catche[i-1] +catche[i-2] 
      }
      return catche[n]
};

343. 整數拆分
給定一個正整數 n，將其拆分為至少兩個正整數的和，並使這些整數的乘積最大化。返回你可以獲得的最大乘積。

示例 1:

輸入: 2
輸出: 1
解釋: 2 = 1 + 1, 1 × 1 = 1。
示例 2:

輸入: 10
輸出: 36
解釋: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36。

解題：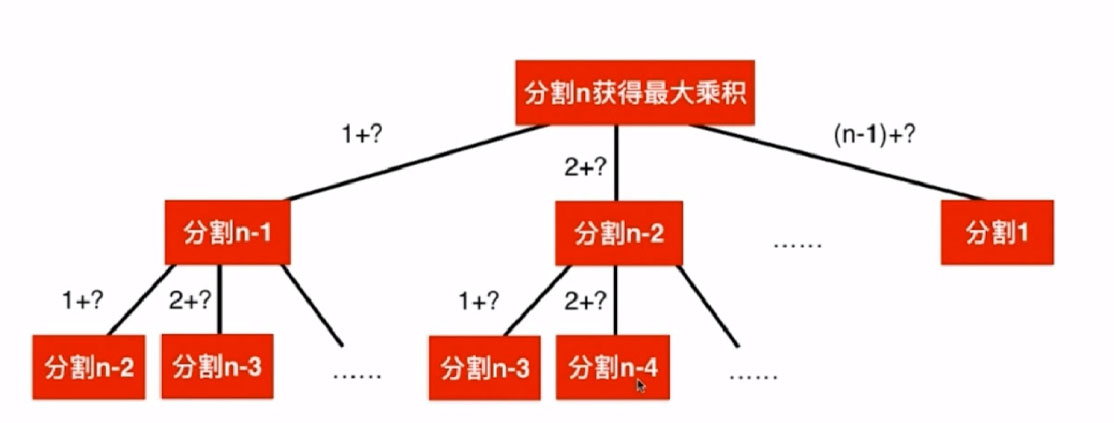

1.我們求分割n獲得的最大乘積，需要求把n分成 1和n-1的成績 2和n-2 的成績到n-1和1的最大成績，在這個結果中取最大值，
2.每次n可以選擇當前值，或者i*(n-i) 不在分割n，和i* 繼續分割n-i的結果i*d(n-i)

3.我們定義dp對象緩存n的最大值的結果，防止重覆求解

/**
 * @param {number} n
 * @return {number}
 */
var integerBreak = function(n) {
     // 定義dp緩存已求解的n的最大值 
     const dp = {}
     function d(n){
          if(n==1){
             return 1
          }
          if(dp[n]!==undefined){
               return dp[n]
          }
          let res = -1
          for(let i =1;i<n;i++){
            res = Math.max(res,i*(n-i),i*d(n-i))
            
          }
          dp[n] = res  
          return dp[n]
     }
     return d(n)
};

解題二

狀態數組dp[i]表示：數字 i 拆分為至少兩個正整數之和的最大乘積。為了方便計算，dp 的長度是 n + 1，值初始化為 1。

顯然dp[2]等於 1，外層迴圈從 3 開始遍歷，一直到 n 停止。內層迴圈 j 從 1 開始遍歷，一直到 i 之前停止，它代表著數字 i 可以拆分成 j + (i - j)。但 j * (i - j)不一定是最大乘積，因為i-j不一定大於dp[i - j]（數字i-j拆分成整數之和的最大乘積），這裡要選擇最大的值作為 dp[i] 的結果。

空間複雜度是 O(N)O(N)，時間複雜度是 O(N^2)O(N的2次方）

/**
 * @param {number} n
 * @return {number}
 */
var integerBreak = function(n) {

    const dp = new Array(n + 1).fill(1);
    for (let i = 3; i <= n; ++i) {
        for (let j = 1; j < i; ++j) {
            // 每次嘗試將n分割為 j+(i-j)的值
            dp[i] = Math.max(dp[i], j * (i - j), j * dp[i - j]);
        }
    }
    return dp[n];

};

198. 打家劫舍
你是一個專業的小偷，計劃偷竊沿街的房屋。每間房內都藏有一定的現金，影響你偷竊的唯一制約因素就是相鄰的房屋裝有相互連通的防盜系統，如果兩間相鄰的房屋在同一晚上被小偷闖入，系統會自動報警。

給定一個代表每個房屋存放金額的非負整數數組，計算你不觸動警報裝置的情況下，一夜之內能夠偷竊到的最高金額。

示例 1：

輸入：[1,2,3,1]
輸出：4
解釋：偷竊 1 號房屋 (金額 = 1) ，然後偷竊 3 號房屋 (金額 = 3)。
偷竊到的最高金額 = 1 + 3 = 4 。

解題：

1. 對於一個房間我們可以選擇偷取也可以選擇不偷取，如果偷取的話我們下次選擇需要選擇n+2的房間來嘗試偷取，結果取最大值

2. 我們求解的值是不考慮偷取當前房間和考慮偷取當前房間的最大值，res = Math.max(res,nums[i]+room(nums,i+2)) ，因為i+2 可能越界，因此當nums.length<=index時我們直接return 0

3.我們用tests 儲存是否已經偷過該房間，如果tests訪問過直接返回值，如果沒有訪問過，我們把求解的n的值儲存在tests中

/**
 * @param {number[]} nums
 * @return {number}
 */
var rob = function(nums) {
     let tests = new Array(nums.length).fill(-1)
     
     function room(nums,index){
         if(nums.length<=index){
             return 0
         }
         if(tests[index]!==-1){
            return tests[index]
         }
         let res = 0
         for(let i =index;i<nums.length;i++){
             res = Math.max(res,nums[i]+room(nums,i+2))
         }
         tests[index] = res
         return tests[index]
 
     }
     
     return room(nums,0)
    
};

解法2

動態規劃方程：dp[n] = MAX( dp[n-1], dp[n-2] + num )
由於不可以在相鄰的房屋闖入，所以在當前位置 n 房屋可盜竊的最大值，要麼就是 n-1 房屋可盜竊的最大值，要麼就是 n-2 房屋可盜竊的最大值加上當前房屋的值，二者之間取最大值
舉例來說：1 號房間可盜竊最大值為 33 即為 dp[1]=3，2 號房間可盜竊最大值為 44 即為 dp[2]=4，3 號房間自身的值為 22 即為 num=2，那麼 dp[3] = MAX( dp[2], dp[1] + num ) = MAX(4, 3+2) = 5，3 號房間可盜竊最大值為 55
時間複雜度：O(n)O(n)，nn 為數組長度

/**
 * @param {number[]} nums
 * @return {number}
 */
var rob = function(nums) {
    const len = nums.length;
    if(len == 0)
        return 0;
    const dp = new Array(len + 1);
    dp[0] = 0;
    dp[1] = nums[0];
    for(let i = 2; i <= len; i++) {
        dp[i] = Math.max(dp[i-1], dp[i-2] + nums[i-1]);
    }
    return dp[len];
};