前言 本篇文章收錄於專輯:http://dwz.win/HjK,點擊解鎖更多數據結構與演算法的知識。 你好,我是彤哥,一個每天爬二十六層樓還不忘讀源碼的硬核男人。 上一節,我們一起學習了表示覆雜度的幾個符號,我們說,通常使用大O來表示演算法的複雜度,不僅合理,而且書寫方便。 那麼,使用大O表示法評估演算法 ...

前言
本篇文章收錄於專輯:http://dwz.win/HjK,點擊解鎖更多數據結構與演算法的知識。
你好,我是彤哥,一個每天爬二十六層樓還不忘讀源碼的硬核男人。
上一節,我們一起學習了表示覆雜度的幾個符號,我們說,通常使用大O來表示演算法的複雜度,不僅合理,而且書寫方便。
那麼,使用大O表示法評估演算法的複雜度有沒有什麼套路呢?以及常見的複雜度有哪些呢?
本節,我們就來解決這兩個問題。
前情回顧
在正式講解套路之前,我們先回憶一下前面幾節講到的內容。
在第2節,我們學習了漸近分析法,將演算法的複雜度與輸入規模掛鉤,隨著輸入規模的增大,演算法執行的時間將呈現一種什麼樣的趨勢,將這個趨勢用函數表示,再去除低階項和常數項,就得到了演算法的時間複雜度。
在第3節,我們分別從最壞、平均、最好三種情況來分析了演算法的複雜度,得出結論,一般使用最壞情況來評估演算法的複雜度。
在第4節,我們通過動態數組的插入元素及經典快速排序的時間複雜度,解釋了有的時候不能使用最壞情況來評估演算法的複雜度。
在第5節,我們從讀音、數學、通俗理解三個方面分析了各種表示演算法複雜度的符號,得出結論還是使用大O比較香,大O代表了演算法的上界,它與前面講到的最壞情況往往是對應的。
所以,這裡所說的套路也是針對大部分情況,也就是最壞情況,對於一些個例,比如經典快排,我們雖然也是使用大O表示他們的複雜度,但是,其實是一種均攤的複雜度。
好了,讓我們看看計算演算法複雜度的套路到底是什麼吧。
套路
我將計算演算法複雜度的套路歸納為以下五步:
- 明確輸入規模n;
- 考慮最壞情況或均攤情況,如果最壞情況為個例,那就是均攤;
- 計算演算法執行的次數與n的關係,並用函數表示出來;
- 去除低階項;
- 去除常數項;
比如,對於在數組中查找指定元素的操作:
- 輸入規模為數組的長度n;
- 考慮最壞情況為目標元素不在數組中;
- 演算法的執行次數為遍歷所有數組元素,也就是n次,用函數表示f(n) = n;
- 去除低階項,沒有低階項,還是n;
- 去除常數項,沒有常數項,還是n;
所以,在數組中查找指定元素的時間複雜度為O(n)。
OK,使用這種方式可以很快的計算出演算法的複雜度,也不需要進行額外的計算,非常快捷高效。
常見的複雜度
上面我們說了,複雜度的計算就是計算與輸入規模n的關係,所以,我們想想數學中關於n的函數就能得出常見的複雜度了,我繪製了一張表格:
| 與n的關係 | 英文釋義 | 複雜度 | 示例 |
|---|---|---|---|
| 常數(不相關) | Constant | O(1) | 數組按索引查找元素 |
| 對數相關 | Logarithmic | O(logn) | 二分查找 |
| 線性相關 | Linear | O(n) | 遍曆數組的元素 |
| 超線性相關 | Superlinear | O(nlogn) | 歸併排序、堆排序 |
| 多項式相關 | Polynomial | O(n^c) | 冒泡排序、插入排序、選擇排序 |
| 指數相關 | Exponential | O(c^n) | 漢諾塔 |
| 階乘相關 | Factorial | O(n!) | 行列式展開 |
| n的n次方 | 無 | O(n^n) | 不知道有沒有這種演算法 |
在這張表中,複雜度是依次增加的,可以看到常數複雜度O(1)無疑是最好的,讓我們用一張圖來直觀感受下:
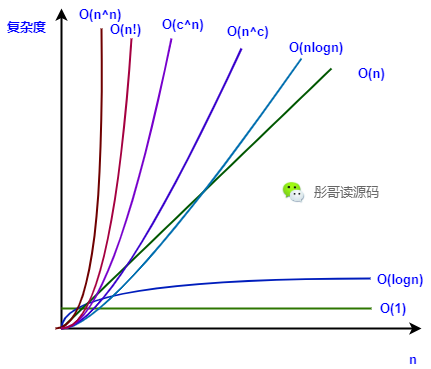
後記
本節,我們一起學習了複雜度分析的套路以及常見的複雜度,到目前為止,我們不管是舉例還是講解基本上都在說時間複雜度。
那麼,空間複雜度又是什麼呢?空間與時間之間如何權衡呢?
下一節,我們接著聊。
關註公號主“彤哥讀源碼”,解鎖更多源碼、基礎、架構知識。



