Floyd演算法詳（cha）解

Floyd 演算法應該是最基本，最簡單，也是最暴力的最短路演算法解法，但是對於一些點數很小的題目，Floyd的表現還是很優秀的，我們先來看一道例題

題目描述給你一個有 \(n\) (\(n\leq 100\)) 個點以及 \(m\) (\(m\leq 800\)) 條雙向邊的圖，求出所有點之間的最短路。
輸入格式：第一行兩個正整數 \(n\),\(m\)，接下來 \(m\) 行，每行三個正整數 \(u\),\(v\),\(w\),表示 \(u\) 和 \(v\) 之間有一條代價（長度）為 \(w\) 的邊。
輸出格式：輸出共 \(n\) 行，每行 \(n\) 個正整數，第 \(i\) 行第 \(j\) 個數，表示點 \(i\) 到點 \(j\) 之間的最短路。
樣例輸入：
5 6
1 3 7
2 4 5
2 3 1
4 3 2
1 5 8
5 2 4
樣例輸出：
0 8 7 9 8
8 0 1 3 4
7 1 0 2 5
9 3 1 0 7
8 4 5 7 0

對於任何一個操作，我們都可以分成三個部分：1.選擇操作容器，2.初始化，3.更新，操作。

比如這一題，讓我們求出 所有點 之間的最短路，並以一個 矩陣型 輸出，所以我們可以考慮就如題目中的那樣，用這個臨接矩陣來儲存，我們把這個矩陣稱為 \(\operatorname{dis}\),用 \(\operatorname{dis[i][j]}\) 來表示 \(\operatorname{i\sim j}\) 之間的最短路徑。

知道了容器，我們就要考慮如何初始化。因為題目讓我們求所有點之間的最短路，所以我們可以初始化 \(\operatorname{dis[i][i]=0}\) （可以理解為，我到我自己，相當於沒動，所以我不需要耗費任何代價），然後每輸入兩個點 \(u\),\(v\)，就將他們輸入的代價，作為最初的 \(\operatorname{dis[u][v]}\) 設置為代價 \(w\),因為在現在看來，這條路是最短的，我們無法從其他地方更新。然後我們考慮一個問題，如果這不是一個 完全圖，也就是說，如果並不是每兩個點之間都有一條連邊，有一些數對(i,j)是沒有直接通路的，我們要怎麼辦？其實非常簡單，如果兩個點一開始沒有直接的連邊，我們就可以將它設置成一個不會被重覆的值（一般為正無窮或者負無窮，看求的東西），也就是 \(\operatorname{dis[u][v]=Inf}\)，於是我們在最開始，就賦值整個數組為正無窮，這樣就可以很方便的預處理完成最初的每兩個點之間的最短路了。

但是，我們這樣並不能直接求出這整個圖每兩點之間的最短路，因為肯定有一些點沒有更新到，並且有一些點之間的最短路點在最後不一定是最短的，這個很好證明，我就不贅述了。於是我們考慮更新，我們拿樣例打比方，我們先建出這個圖：

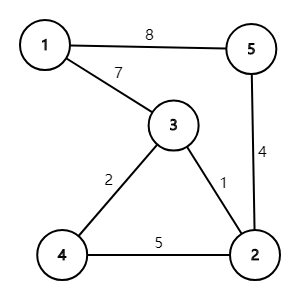
然後按照剛剛的方法初始化一下這個矩陣每個點之間的最初的最短路,大概是這個樣子的：

0 ∞ ∞ ∞ ∞ --> 0 ∞ 7 ∞ 8
∞ 0 ∞ ∞ ∞ --> ∞ 0 1 5 4
∞ ∞ 0 ∞ ∞ --> 7 1 0 2 ∞
∞ ∞ ∞ 0 ∞ --> ∞ 5 2 0 ∞
∞ ∞ ∞ ∞ 0 --> 8 4 ∞ ∞ 0

然後就是這個演算法最重要的部分了，我們考慮如何更新兩個點之間的最短路，來看下麵這個簡化的圖：

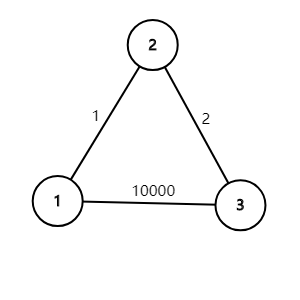
在這個圖中，\(1\sim3\) 之間初試化的最短路是 \(10000\),顯然，當我們重新選擇 \(1\sim 2\sim3\) 這條路的時候,代價就減小到了 \(3\)，比之前那條道路更優秀。這就相當於是在點 \(1\) 和 \(3\) 之間，找到一個新的點加入，用 \(1\sim 2\) 與 \(2\sim3\) 來更新這個最短路，可以算作是一種 區間dp 的思想。Floyd 的核心思想就是這個，就是在 兩點之間加上一個點 然後和之前的最短路作比較，然後不斷更新，達到求出全源最短路的效果。

我們再將這種演算法放回原樣例中去驗證一下，我們從1-n 枚舉每個節點 \(k\) ，用來更新兩個點之間是否還有更短的路徑。我們從 \(1\) 開始，我們來看一遍。

用 1 更新：
0 ∞ 7 ∞ 8 --> 0 ∞ 7 ∞ 8
∞ 0 1 5 4 --> ∞ 0 1 5 4
7 1 0 2 ∞ --> 7 1 0 2 ∞
∞ 5 2 0 ∞ --> ∞ 5 2 0 ∞
8 4 ∞ ∞ 0 --> 8 4 ∞ ∞ 0

用 2 更新：
0 ∞ 7 ∞ 8 --> 0 ∞ 7 ∞ 8
∞ 0 1 5 4 --> ∞ 0 1 5 4
7 1 0 2 ∞ --> 7 1 0 2 5
∞ 5 2 0 ∞ --> ∞ 5 2 0 9
8 4 ∞ ∞ 0 --> 8 4 5 9 0

用 3 更新:
0 ∞ 7 ∞ 8 --> 0 8 7 9 8
∞ 0 1 5 4 --> 8 0 1 3 4
7 1 0 2 5 --> 7 1 0 2 5
∞ 5 2 0 9 --> 9 3 2 0 7
8 4 ∞ ∞ 0 --> 8 4 5 7 0

用 4 更新：
0 8 7 9 8 --> 0 8 7 9 8
8 0 1 3 4 --> 8 0 1 3 4
7 1 0 2 5 --> 7 1 0 2 5
9 3 2 0 7 --> 9 3 2 0 7
8 4 5 7 0 --> 8 4 5 7 0

用 5 更新：
0 8 7 9 8 --> 0 8 7 9 8
8 0 1 3 4 --> 8 0 1 3 4
7 1 0 2 5 --> 7 1 0 2 5
9 3 2 0 7 --> 9 3 2 0 7
8 4 5 7 0 --> 8 4 5 7 0

（大家可以配著圖來理解）[加粗數字為更新過的最短路]

看起來沒什麼問題實際也沒什麼問題，於是我們開是碼代碼吧。

先是初始化：

memset(dis,0x3f3f3f3f,sizeof(dis));
for(int i=1;i<=n;i++)dis[i][i]=0;
for(int i=1;i<=n;i++)int u,v,w,scanf("%d%d%d",&u,&v,&w),dis[u][v]=w;

第一行就是初始化 \(\operatorname{dis}\) 都為正無窮,0x3f3f3f3f是16進位中的一個數，差不多接近了 INT_MAX 了。
第二行就是自己到自己的最短路
第三行是輸入與每兩個點之間的最短路初始化。

然後就是 Floyd 啦：

for(int k=1;k<=n;k++)//首先枚舉中間加入的點，不然會出錯
      for(int i=1;i<=n;i++)//然後i,j是枚舉每個點，算 i~j 之間的最短路 
            for(int j=1;j<=n;j++)
                 dis[i][j]=min(dis[i][j],dis[i][k]+dis[k][j]);//Floyd的狀態轉移方程，這是精華，一定要記牢

這些上面已經講過了，沒懂的可以多看幾遍。
看懂了的完整代碼應該不難寫了，所以整塊的代碼就不放了。

下麵給出幾個例題：

• luogu P2888 [USACO07NOV]Cow Hurdles S
• luogu P2935 [USACO09JAN]Best Spot S
• luogu P1522 [USACO2.4]牛的旅行 Cow Tours

當然，Floyd的功能肯定不止求最短路，它還可以做很多的事情，比如下麵這道題：

有 \(n\)（\(n\leq 100\)） 個人，他們之間會有 \(m\) (\(m\leq 800\)) 場比賽，當一個人比了 \(n-1\) 場比賽後，他就能確定自己的名次，試問共有幾個人知道自己的名次？
輸入格式：第一行兩個正整數 \(n\),\(m\)。接下來 \(m\) 行 每行兩行兩個 \(\leq n\) 的正整數，表示這兩個人之間有一場比賽。
輸出格式：一個正整數，表示知道自己名次的人的個數。
樣例輸入：
5 5
4 3
4 2
3 2
1 2
2 5
樣例輸出：
2

乍一看沒啥思路，但是看到這個數據範圍，明顯就是放 \(n^3\) 的演算法過嗎，而且這個題目還可以抽象成求 有幾個點與其他點都相領 的圖論問題，所以我們考慮使用 Floyd 演算法。
我們按照 Floyd 的方法建圖看，將每兩條直接連通的邊的權值設為 true,不連通就是 \(flase\)（應該很好理解吧？）。
接下來，我們考慮如何轉移狀態。按照Floyd的思想，如果兩點之間沒有直接連邊，但是可以通過 加入一個點 來使他們連通，這兩個點就是聯通的，我們將他抽象成代碼。dis[i][j]為true，必須保證 dis[i][j] 本身為true 或者在他們之間加上點 \(k\),讓 dis[i][k] 為true,dis[k][j] 也為true,所以我們得到了以下轉移方程：

dis[i][j]=dis[i][j]|(dis[i][k]&dis[k][j]);

| 表示左右兩個條件中只要有一個為 真，這個值就為 真。
& 表示左右兩個條件中都要為 真，這個值才是 真。

來看下這一題的完整代碼：

#include<bits/stdc++.h>
using namespace std;
const int INF=99999999;
const int Inf=0x3f3f3f3f;
const int maxn=305;
const int maxm=25005;
int n,m,t;int dis[maxn][maxn];
int head[maxn],cnt;
int ans;
struct node
{
	int nxt,to,w;
}e[maxm];//鏈式前向星存圖，不會的可以直接用dis存。
int times[maxn];
inline void add(int u,int v,int w)
{
	e[++cnt].to=v;
	e[cnt].nxt=head[u];
	e[cnt].w=w;
	head[u]=cnt; 
}//鏈式前向星加邊操作
inline void get(int u)
{
	for(int i=head[u];i;i=e[i].nxt)
	{
		dis[u][e[i].to]=e[i].w;
	}
}//對於每條邊的權值，都講他加入dis里
int main()
{
	scanf("%d %d",&n,&m);
	for(int i=1;i<=m;i++)
	{
		int u,v;scanf("%d %d",&u,&v);
		add(u,v,1);
	}
	for(int i=1;i<=n;i++)
	{
		get(i);
	}//預處理dis數組的邊權
	for(int k=1;k<=n;k++)
	{
		for(int i=1;i<=n;i++)
		{
			for(int j=1;j<=n;j++)
			{
				dis[i][j]=dis[i][j]|dis[i][k]&dis[k][j];//狀態轉移方程&Floyd
			}
		}
	}
	for(int i=1;i<=n;i++)
	{
		int p=1;
		for(int j=1;j<=n;j++)
		{
			if(i==j)continue;
			p=p&(dis[i][j]|dis[j][i]);只要這兩條邊中有一個是聯通的，這兩點就是聯通的
		}
		ans+=p;
	}
	printf("%d\n",ans);
} 

給出題目鏈接：

• luogu P2419 [USACO08JAN]Cow Contest S