前言 遞歸,是一個非常重要的概念,也是面試中非常喜歡考的。因為它不但能考察一個程式員的演算法功底,還能很好的考察對時間空間複雜度的理解和分析。 本文只講一題,也是幾乎所有演算法書講遞歸的第一題,但力爭講出花來,在這裡分享四點不一樣的角度,讓你有不同的收穫。 時空複雜度的詳細分析 識別並簡化遞歸過程中的重 ...
前言
遞歸,是一個非常重要的概念,也是面試中非常喜歡考的。因為它不但能考察一個程式員的演算法功底,還能很好的考察對時間空間複雜度的理解和分析。
本文只講一題,也是幾乎所有演算法書講遞歸的第一題,但力爭講出花來,在這裡分享四點不一樣的角度,讓你有不同的收穫。
- 時空複雜度的詳細分析
- 識別並簡化遞歸過程中的重覆運算
- 披上羊皮的狼
- 適當炫技助我拿到第一份工作
演算法思路
大家都知道,一個方法自己調用自己就是遞歸,沒錯,但這隻是理解遞歸的最表層的理解。
那麼遞歸的實質是什麼?
答:遞歸的實質是能夠把一個大問題分解成比它小點的問題,然後我們拿到了小問題的解,就可以用小問題的解去構造大問題的解。
那小問題的解是如何得到的?
答:用再小一號的問題的解構造出來的,小到不能再小的時候就是到了零號問題的時候,也就是 base case 了。
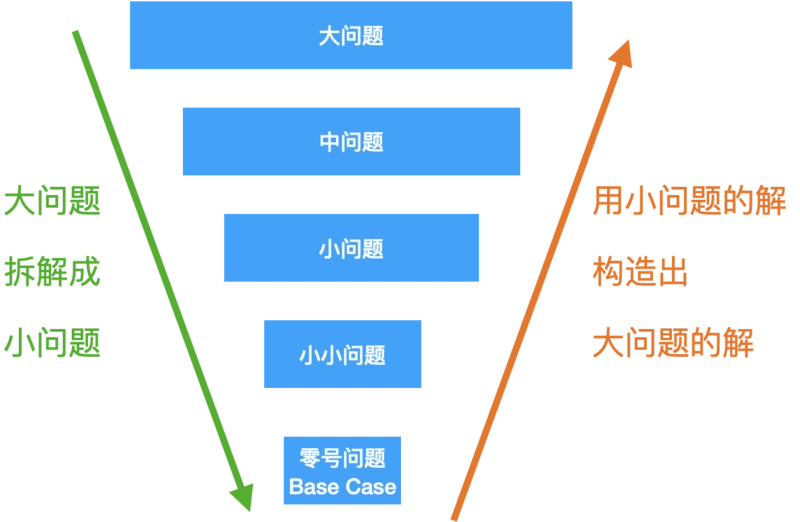
那麼總結一下遞歸的三個步驟:
Base case:就是遞歸的零號問題,也是遞歸的終點,走到最小的那個問題,能夠直接給出結果,不必再往下走了,否則,就會成死迴圈;
拆解:每一層的問題都要比上一層的小,不斷縮小問題的 size,才能從大到小到 base case;
組合:得到了小問題的解,還要知道如何才能構造出大問題的解。
所以每道遞歸題,我們按照這三個步驟來分析,把這三個問題搞清楚,代碼就很容易寫了。
斐波那契數列
這題雖是老生常談了,但相信我這裡分享的一定會讓你有其他收穫。
題目描述
斐波那契數列是一位義大利的數學家,他閑著沒事去研究兔子繁殖的過程,研究著就發現,可以寫成這麼一個序列:1,1,2,3,5,8,13,21…也就是每個數等於它前兩個數之和。那麼給你第 n 個數,問 F(n) 是多少。
解析
用數學公式表示很簡單:
f(n) = f(n-1) + f(n-2)
代碼也很簡單,用我們剛總結的三步:
- base case: f(0) = 0, f(1) = 1.
- 分解:f(n-1), f(n-2)
- 組合:f(n) = f(n-1) + f(n-2)
那麼寫出來就是:
class Solution {
public int fib(int N) {
if (N == 0) {
return 0;
} else if (N == 1) {
return 1;
}
return fib(N-1) + fib(N-2);
}
}
但是這種解法 Leetcode 給出的速度經驗只比 15% 的答案快,因為,它的時間複雜度實在是太高了!

過程分析
那這就是我想分享的第一點,如何去分析遞歸的過程。
首先我們把這顆 Recursion Tree 畫出來,比如我們把 F(5) 的遞歸樹畫出來:
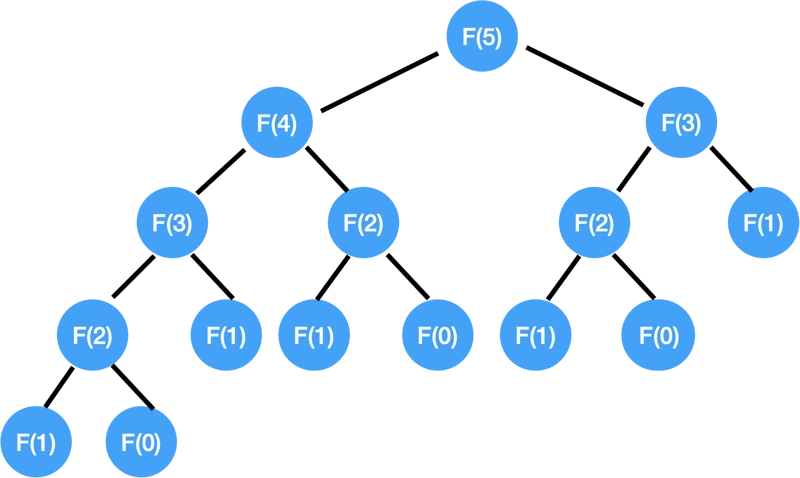
那實際的執行路線是怎樣的?
首先是沿著最左邊這條線一路到底:F(5) → F(4) → F(3) → F(2) → F(1),好了終於有個 base case 可以返回 F(1) = 1 了,然後返回到 F(2) 這一層,再往下走,就是 F(0),又觸底反彈,回到 F(2),得到 F(2) = 1+0 =1 的結果,把這個結果返回給 F(3),然後再到 F(1),拿到結果後再返回 F(3) 得到 F(3) = 左 + 右 = 2,再把這個結果返上去...
這種方式本質上是由我們電腦的馮諾伊曼體系造就的,目前一個 CPU 一個核在某一時間只能執行一條指令,所以不能 F(3) 和 F(4) 一起進行了,一定是先執行了 F(4) (本代碼把 fib(N-1) 放在前面),再去執行 F(3).
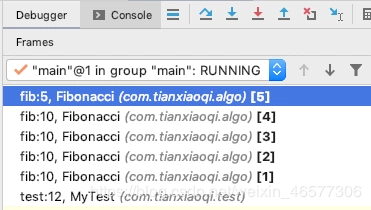
我們在 IDE 里 debug 就可以看到棧裡面的情況:這裡確實是先走的最左邊這條線路,一共有 5 層,然後再一層層往上返回。
時間複雜度分析
如何評價一個演算法的好壞?
很多問題都有多種解法,畢竟條條大路通羅馬。但如何評價每種方法的優劣,我們一般是用大 O 表達式來衡量時間和空間複雜度。
時間複雜度:隨著自變數的增長,所需時間的增長情況。
這裡大 O 表示的是一個演算法在 worst case 的表現情況,這就是我們最關心的,不然春運搶車票的時候系統 hold 不住了,你跟我說這個演算法很優秀?
當然還有其他衡量時間和空間的方式,比如
Theta: 描述的是 tight bound Omega(n):
這個描述的是 best case,最好的情況,沒啥意義
這也給我們了些許啟發,不要說你平時表現有多好,沒有意義;面試衡量的是你在 worst case 的水平;不要說面試沒有發揮出你的真實水平,扎心的是那就是我們的真實水平。
那對於這個題來說,時間複雜度是多少呢?
答:因為我們每個節點都走了一遍,所以是把所有節點的時間加起來就是總的時間。
在這裡,我們在每個節點上做的事情就是相加求和,是 O(1) 的操作,且每個節點的時間都是一樣的,所以:
總時間 = 節點個數 * 每個節點的時間
那就變成了求節點個數的數學題:
在 N = 5 時,
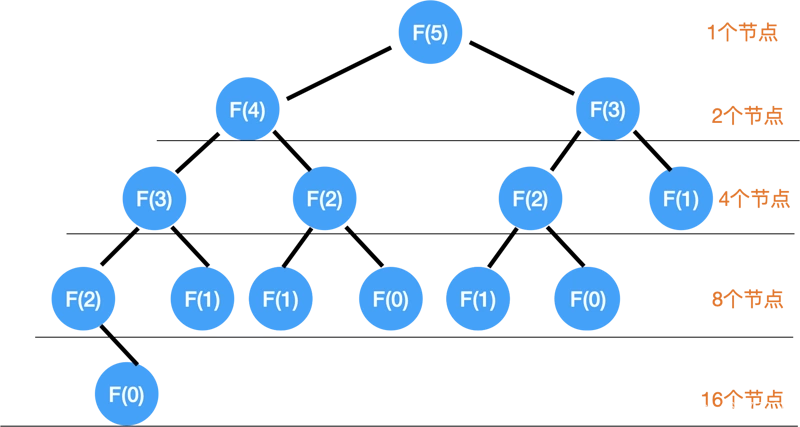
最上面一層有1個節點,
第二層 2 個,
第三層 4 個,
第四層 8 個,
第五層 16 個,如果填滿的話,想象成一顆很大的樹:)
這裡就不要在意這個沒填滿的地方了,肯定是會有差這麼幾個 node,但是大 O 表達的時間複雜度我們剛說過了,求的是 worst case.
那麼總的節點數就是:
1 + 2 + 4 + 8 + 16
這就是一個等比數列求和了,當然你可以用數學公式來算,但還有個小技巧可以幫助你快速計算:
其實前面每一層的節點相加起來的個數都不會超過最後一層的節點的個數,總的節點數最多也就是最後一層節點數 * 2,然後在大 O 的時間複雜度裡面常數項也是無所謂的,所以這個總的時間複雜度就是:
最後一層節點的個數:2^n
空間複雜度分析
一般書上寫的空間複雜度是指:
演算法運行期間所需占用的所有記憶體空間
但是在公司里大家常用的,也是面試時問的指的是
Auxiliary space complexity:
運行演算法時所需占用的額外空間。
舉例說明區別:比如結果讓你輸出一個長度為 n 的數組,那麼這 O(n) 的空間是不算在演算法的空間複雜度里的,因為這個空間是跑不掉的,不是取決於你的演算法的。
那空間複雜度怎麼分析呢?
我們剛剛說到了馮諾伊曼體系,從圖中也很容易看出來,是最左邊這條路線占用 stack 的空間最多,一直不斷的壓棧,也就是從 5 到 4 到 3 到 2 一直壓到 1,才到 base case 返回,每個節點占用的空間複雜度是 O(1),所以加起來總的空間複雜度就是 O(n).
優化演算法
那我們就想了,為什麼這麼一個簡簡單單的運算竟然要指數級的時間複雜度?到底是為什麼讓時間如此之大。
那也不難看出來,在這棵 Recursion Tree 里,有太多的重覆計算了。
比如一個 F(2) 在這裡都被計算了 3 次,F(3) 被計算了 2 次,每次還都要再重新算,這不就是狗熊掰棒子嗎,真的是一把辛酸淚。
那找到了原因之後,為瞭解決這種重覆計算,電腦採用的方法其實和我們人類是一樣的:記筆記。
對很多職業來說,比如醫生、律師、以及我們工程師,為什麼越老經驗值錢?因為我們見得多積累的多,下次再遇到類似的問題時,能夠很快的給出解決方案,哪怕一時解決不了,也避免了一些盲目的試錯,我們會站在過去的高度不斷進步,而不是每次都從零開始。
回到優化演算法上來,那電腦如何記筆記呢?
我們要想求 F(n),無非也就是要
記錄 F(0) ~ F(n-1) 的值,
那選取一個合適的數據結構來存儲就好了。
那這裡很明顯了,用一個數組來存:
| Index | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| F(n) | 0 | 1 | 1 | 2 | 3 | 5 |
那有了這個 cheat sheet,我們就可以從前到後得到結果了,這樣每一個點就只算了一遍,用一個 for loop 就可以寫出來,代碼也非常簡單。
class Solution {
public int fib(int N) {
if (N == 0) {
return 0;
}
if (N== 1) {
return 1;
}
int[] notes = new int[N+1];
notes[0] = 0;
notes[1] = 1;
for(int i = 2; i <= N; i++) {
notes[i] = notes[i-1] + notes[i-2];
}
return notes[N];
}
}
這個速度就是 100% 了~
但是我們可以看到,空間應該還有優化的餘地。
那仔細想想,其實我們記筆記的時候需要記錄這麼多嗎?需要從幼兒園到小學到初中到高中的筆記都留著嗎?
那其實每項的計算只取決於它前面的兩項,所以只用保留這兩個就好了。
那我們可以用一個長度為 2 的數組來計算,或者就用 2 個變數。
更新代碼:
class Solution {
public int fib(int N) {
int a = 0;
int b = 1;
if(N == 0) {
return a;
}
if(N == 1) {
return b;
}
for(int i = 2; i <= N; i++) {
int tmp = a + b;
a = b;
b = tmp;
}
return b;
}
}
這樣我們就把空間複雜度優化到了 O(1),時間複雜度和用數組記錄一樣都是 O(n).
這種方法其實就是動態規劃 Dynamic Programming,寫出來的代碼非常簡單。
那我們比較一下 Recursion 和 DP:
Recursion 是從大到小,層層分解,直到 base case 分解不了了再組合返回上去;
DP 是從小到大,記好筆記,不斷進步。
也就是 Recursion + Cache = DP
如何記錄這個筆記,如何高效的記筆記,這是 DP 的難點。
有人說 DP 是拿空間換時間,但我不這麼認為,這道題就是一個很好的例證。
在用遞歸解題時,我們可以看到,空間是 O(n) 在棧上的,但是用 DP 我們可以把空間優化到 O(1),DP 可以做到時間空間的雙重優化。
其實呢,斐波那契數列在現實生活中也有很多應用。
比如在我司以及很多大公司里,每個任務要給分值,1分表示大概需要花1天時間完成,然後分值只有>1,2,3,5,8這5種,(如果有大於8分的任務,就需要把它 break down 成8分以內的,以便大家在>兩周內能完成。)
因為任務是永遠做不完的而每個人的時間是有限的,所以每次小組會開會,挑出最重要的任務讓大家來>做,然後每個人根據自己的 available 的天數去 pick up 相應的任務。
那有同學可能會想,這題這麼簡單,這都 2020 年了,面試還會考麽?
答:真的會。
只是不能以這麼直白的方式給你了。
比如很有名的爬樓梯問題:
一個 N 階的樓梯,每次能走一層或者兩層,問一共有多少種走法。
這個題這麼想:
站在當前位置,只能是從前一層,或者前兩層上來的,所以 f(n) = f(n-1) + f(n-2).
這題是我當年面試時真實被問的,那時我還在寫 python,為了炫技,還用了lambda function:
f = lambda n: 1 if n in (1, 2) else f(n-1) + f(n-2)
遞歸的寫法時間複雜度太高,所以又寫了一個 for loop 的版本
def fib(n)
a, b = 1, 1
for i in range(n-1):
a, b = b, a+b
return a
然後還寫了個 caching 的方法:
def cache(f):
memo = {}
def helper(x):
if x not in memo:
memo[x] = f(x)
return memo[x]
return helper
@cache
def fibR(n):
if n==1 or n==2: return 1
return fibR(n-1) + fibR(n-2)
還順便和麵試官聊了下 tail recursion:
tail recursion 尾遞歸:就是遞歸的這句話是整個方法的最後一句話。
那這個有什麼特別之處呢?
尾遞歸的特點就是我們可以很容易的把它轉成 iterative 的寫法,當然有些智能的編譯器會自動幫我們做了(不是說顯性的轉化,而是在運行時按照 iterative 的方式去運行,實際消耗的空間是O(1))
那為什麼呢?
因為回來的時候不需要 backtrack,遞歸這裡就是最後一步了,不需要再往上一層返值。
def fib(n, a=0, b=1):
if n==0: return a
if n==1: return b
return fib(n-1, b, a+b)
最終,拿出了我的殺手鐧:lambda and reduce
fibRe = lambda n: reduce(lambda x, n: [x[1], x[0]+x[1]], range(n), [0, 1])
看到面試官滿意的表情後,就開始繼續深入的聊了...
所以說,不要以為它簡單,同一道題可以用七八種方法來解,分析好每個方法的優缺點,引申到你可以引申的地方,展示自己扎實的基本功,這場面試其實就是你 show off 的機會,這樣才能騙過面試官啊~lol
這就是本文的所有內容了,不知道大家看完感受如何?留言告訴我你的感受吧~
點擊在看,鼓勵下我啊!
瞎寫評論,顯得我很紅啊!
轉發轉發轉發,愛她,就送給她!
還想跟我看更多數據結構和演算法題的小伙伴們,記得關註我,我是程式零世界,演算法就這麼回事。
作者:小齊本齊



