B樹和B+樹的插入、刪除圖文詳解

本文摘自:https://www.cnblogs.com/nullzx/p/8729425.html

感謝大佬nullzx的總結與分享。

另外為驗證本人的正確性,通過一個小工具驗證了下文中的拆入結果，感興趣的伙伴們 可以自己動手驗證。

B-Trees

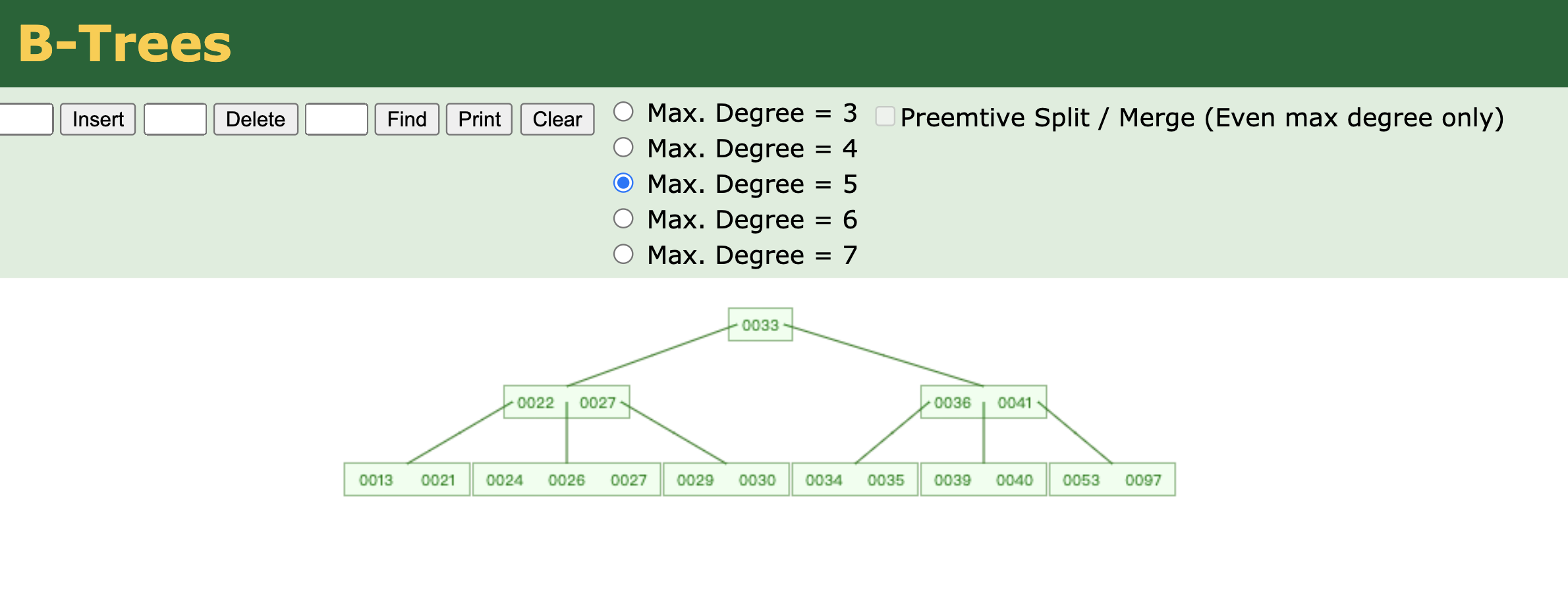
簡介：本文主要介紹了B樹和B+樹的插入、刪除操作。寫這篇博客的目的是發現沒有相關博客以舉例的方式詳細介紹B+樹的相關操作，由於自身對某些細節也感到很迷惑，通過查閱相關資料，對B+樹的操作有所頓悟，寫下這篇博客以做記錄。由於是自身對B+樹的理解，肯定有考慮不周的情況，或者理解錯誤的地方，請留言指出。

1、B樹

B樹的定義

B樹也稱B-樹,它是一顆多路平衡查找樹。我們描述一顆B樹時需要指定它的階數，階數表示了一個結點最多有多少個孩子結點，一般用字母m表示階數。當m取2時，就是我們常見的二叉搜索樹。

一顆m階的B樹定義如下：

1）每個結點最多有m-1個關鍵字。

2）根結點最少可以只有1個關鍵字。

3）非根結點至少有Math.ceil(m/2)-1個關鍵字。

4）每個結點中的關鍵字都按照從小到大的順序排列，每個關鍵字的左子樹中的所有關鍵字都小於它，而右子樹中的所有關鍵字都大於它。

5）所有葉子結點都位於同一層，或者說根結點到每個葉子結點的長度都相同。

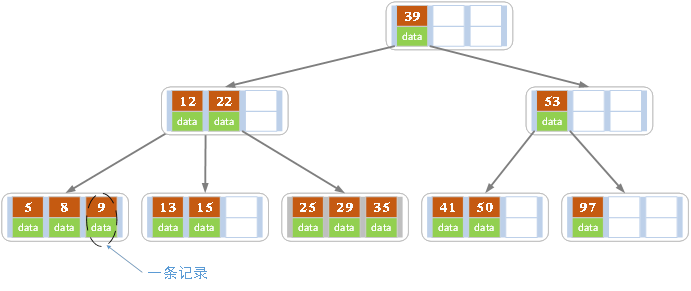
上圖是一顆階數為4的B樹。在實際應用中的B樹的階數m都非常大（通常大於100），所以即使存儲大量的數據，B樹的高度仍然比較小。每個結點中存儲了關鍵字（key）和關鍵字對應的數據（data），以及孩子結點的指針。我們將一個key和其對應的data稱為一個記錄。但為了方便描述，除非特別說明，後續文中就用key來代替（key, value）鍵值對這個整體。在資料庫中我們將B樹（和B+樹）作為索引結構，可以加快查詢速速，此時B樹中的key就表示鍵，而data表示了這個鍵對應的條目在硬碟上的邏輯地址。

B樹的插入操作

插入操作是指插入一條記錄，即（key, value）的鍵值對。如果B樹中已存在需要插入的鍵值對，則用需要插入的value替換舊的value。若B樹不存在這個key,則一定是在葉子結點中進行插入操作。

1）根據要插入的key的值，找到葉子結點並插入。

2）判斷當前結點key的個數是否小於等於m-1，若滿足則結束，否則進行第3步。

3）以結點中間的key為中心分裂成左右兩部分，然後將這個中間的key插入到父結點中，這個key的左子樹指向分裂後的左半部分，這個key的右子支指向分裂後的右半部分，然後將當前結點指向父結點，繼續進行第3步。

下麵以5階B樹為例，介紹B樹的插入操作，在5階B樹中，結點最多有4個key,最少有2個key

a）在空樹中插入39，此時根結點就一個key，此時根結點也是葉子結點

b）繼續插入22，97和41，根結點此時有4個key

c）繼續插入53

插入後超過了最大允許的關鍵字個數4，所以以key值為41為中心進行分裂，結果如下圖所示，分裂後當前結點指針指向父結點，滿足B樹條件，插入操作結束。當階數m為偶數時，需要分裂時就不存在排序恰好在中間的key，那麼我們選擇中間位置的前一個key或中間位置的後一個key為中心進行分裂即可。

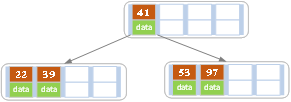
d）依次插入13，21，40，同樣會造成分裂，結果如下圖所示。

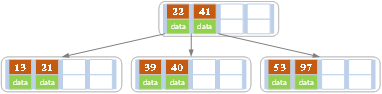
e）依次插入30，27, 33 ；36，35，34 ；24，29，結果如下圖所示。

f）插入key值為26的記錄，插入後的結果如下圖所示。

當前結點需要以27為中心分裂，並向父結點進位27，然後當前結點指向父結點，結果如下圖所示。

進位後導致當前結點（即根結點）也需要分裂，分裂的結果如下圖所示。

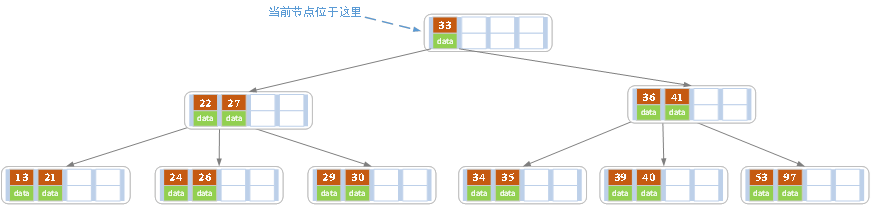
分裂後當前結點指向新的根，此時無需調整。

g）最後再依次插入key為17,28,29,31,32的記錄，結果如下圖所示。

在實現B樹的代碼中，為了使代碼編寫更加容易，我們可以將結點中存儲記錄的數組長度定義為m而非m-1，這樣方便底層的結點由於分裂向上層插入一個記錄時，上層有多餘的位置存儲這個記錄。同時，每個結點還可以存儲它的父結點的引用，這樣就不必編寫遞歸程式。

一般來說，對於確定的m和確定類型的記錄，結點大小是固定的，無論它實際存儲了多少個記錄。但是分配固定結點大小的方法會存在浪費的情況，比如key為28,29所在的結點，還有2個key的位置沒有使用，但是已經不可能繼續在插入任何值了，因為這個結點的前序key是27,後繼key是30,所有整數值都用完了。所以如果記錄先按key的大小排好序，再插入到B樹中，結點的使用率就會很低，最差情況下使用率僅為50%。

B樹的刪除操作

刪除操作是指，根據key刪除記錄，如果B樹中的記錄中不存對應key的記錄，則刪除失敗。

1）如果當前需要刪除的key位於非葉子結點上，則用後繼key（這裡的後繼key均指後繼記錄的意思）覆蓋要刪除的key，然後在後繼key所在的子支中刪除該後繼key。此時後繼key一定位於葉子結點上，這個過程和二叉搜索樹刪除結點的方式類似。刪除這個記錄後執行第2步

2）該結點key個數大於等於Math.ceil(m/2)-1，結束刪除操作，否則執行第3步。

3）如果兄弟結點key個數大於Math.ceil(m/2)-1，則父結點中的key下移到該結點，兄弟結點中的一個key上移，刪除操作結束。

否則，將父結點中的key下移與當前結點及它的兄弟結點中的key合併，形成一個新的結點。原父結點中的key的兩個孩子指針就變成了一個孩子指針，指向這個新結點。然後當前結點的指針指向父結點，重覆上第2步。

有些結點它可能即有左兄弟，又有右兄弟，那麼我們任意選擇一個兄弟結點進行操作即可。

下麵以5階B樹為例，介紹B樹的刪除操作，5階B樹中，結點最多有4個key,最少有2個key

a）原始狀態

b）在上面的B樹中刪除21，刪除後結點中的關鍵字個數仍然大於等2，所以刪除結束。

c）在上述情況下接著刪除27。從上圖可知27位於非葉子結點中，所以用27的後繼替換它。從圖中可以看出，27的後繼為28，我們用28替換27，然後在28（原27）的右孩子結點中刪除28。刪除後的結果如下圖所示。

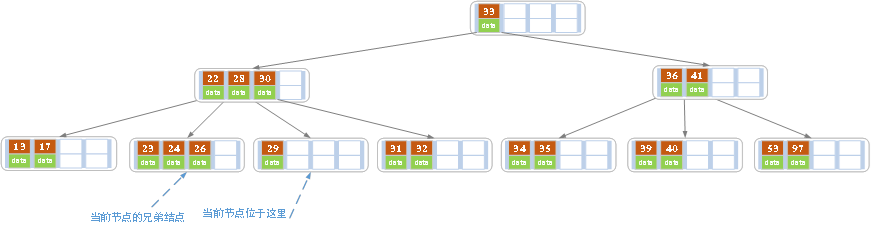
刪除後發現，當前葉子結點的記錄的個數小於2，而它的兄弟結點中有3個記錄（當前結點還有一個右兄弟，選擇右兄弟就會出現合併結點的情況，不論選哪一個都行，只是最後B樹的形態會不一樣而已），我們可以從兄弟結點中借取一個key。所以父結點中的28下移，兄弟結點中的26上移,刪除結束。結果如下圖所示。

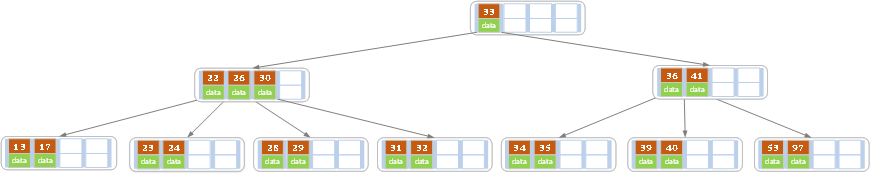
d）在上述情況下接著32，結果如下圖。

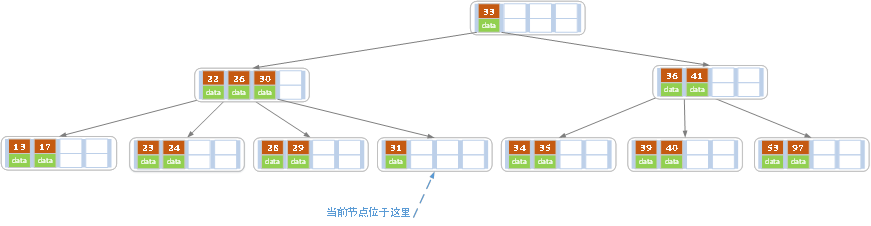
當刪除後，當前結點中只key，而兄弟結點中也僅有2個key。所以只能讓父結點中的30下移和這個兩個孩子結點中的key合併，成為一個新的結點，當前結點的指針指向父結點。結果如下圖所示。

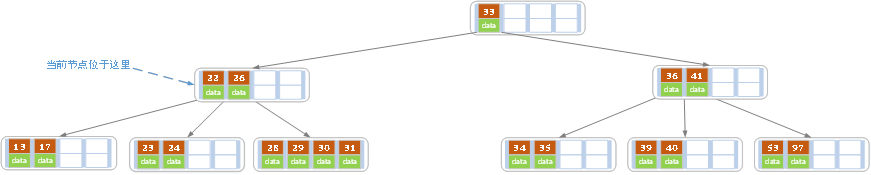
當前結點key的個數滿足條件，故刪除結束。

e）上述情況下，我們接著刪除key為40的記錄，刪除後結果如下圖所示。

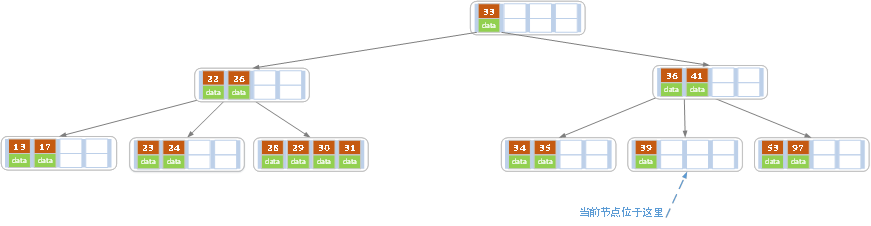
同理，當前結點的記錄數小於2，兄弟結點中沒有多餘key，所以父結點中的key下移，和兄弟（這裡我們選擇左兄弟，選擇右兄弟也可以）結點合併，合併後的指向當前結點的指針就指向了父結點。

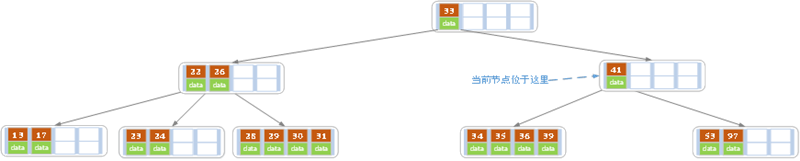
同理，對於當前結點而言只能繼續合併了，最後結果如下所示。

合併後結點當前結點滿足條件，刪除結束。

2. B+樹

B+樹的定義

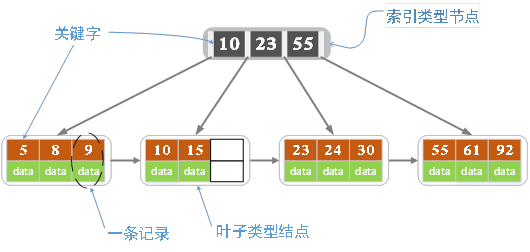
各種資料上B+樹的定義各有不同，一種定義方式是關鍵字個數和孩子結點個數相同。這裡我們採取維基百科上所定義的方式，即關鍵字個數比孩子結點個數小1，這種方式是和B樹基本等價的。上圖就是一顆階數為4的B+樹。

除此之外B+樹還有以下的要求。

1）B+樹包含2種類型的結點：內部結點（也稱索引結點）和葉子結點。根結點本身即可以是內部結點，也可以是葉子結點。根結點的關鍵字個數最少可以只有1個。

2）B+樹與B樹最大的不同是內部結點不保存數據，只用於索引，所有數據（或者說記錄）都保存在葉子結點中。

3） m階B+樹表示了內部結點最多有m-1個關鍵字（或者說內部結點最多有m個子樹），階數m同時限制了葉子結點最多存儲m-1個記錄。

4）內部結點中的key都按照從小到大的順序排列，對於內部結點中的一個key，左樹中的所有key都小於它，右子樹中的key都大於等於它。葉子結點中的記錄也按照key的大小排列。

5）每個葉子結點都存有相鄰葉子結點的指針，葉子結點本身依關鍵字的大小自小而大順序鏈接。

B+樹的插入操作

1）若為空樹，創建一個葉子結點，然後將記錄插入其中，此時這個葉子結點也是根結點，插入操作結束。

2）針對葉子類型結點：根據key值找到葉子結點，向這個葉子結點插入記錄。插入後，若當前結點key的個數小於等於m-1，則插入結束。否則將這個葉子結點分裂成左右兩個葉子結點，左葉子結點包含前m/2個記錄，右結點包含剩下的記錄，將第m/2+1個記錄的key進位到父結點中（父結點一定是索引類型結點），進位到父結點的key左孩子指針向左結點,右孩子指針向右結點。將當前結點的指針指向父結點，然後執行第3步。

3）針對索引類型結點：若當前結點key的個數小於等於m-1，則插入結束。否則，將這個索引類型結點分裂成兩個索引結點，左索引結點包含前(m-1)/2個key，右結點包含m-(m-1)/2個key，將第m/2個key進位到父結點中，進位到父結點的key左孩子指向左結點, 進位到父結點的key右孩子指向右結點。將當前結點的指針指向父結點，然後重覆第3步。

下麵是一顆5階B樹的插入過程，5階B數的結點最少2個key，最多4個key。

a）空樹中插入5

b）依次插入8，10，15

c）插入16

插入16後超過了關鍵字的個數限制，所以要進行分裂。在葉子結點分裂時，分裂出來的左結點2個記錄，右邊3個記錄，中間key成為索引結點中的key，分裂後當前結點指向了父結點（根結點）。結果如下圖所示。

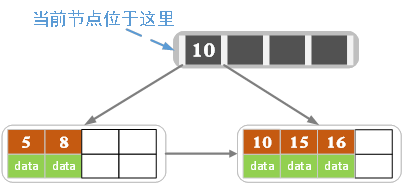
當然我們還有另一種分裂方式，給左結點3個記錄，右結點2個記錄，此時索引結點中的key就變為15。

d）插入17

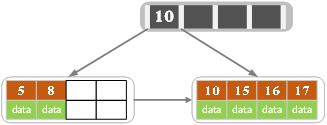
e）插入18，插入後如下圖所示

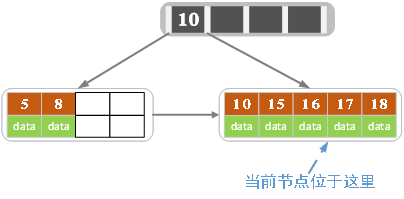
當前結點的關鍵字個數大於5，進行分裂。分裂成兩個結點，左結點2個記錄，右結點3個記錄，關鍵字16進位到父結點（索引類型）中，將當前結點的指針指向父結點。

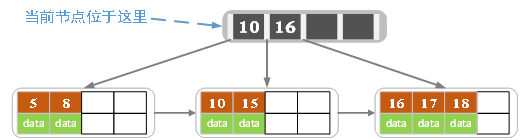
當前結點的關鍵字個數滿足條件，插入結束。

f）插入若幹數據後

g）在上圖中插入7，結果如下圖所示

當前結點的關鍵字個數超過4，需要分裂。左結點2個記錄，右結點3個記錄。分裂後關鍵字7進入到父結點中，將當前結點的指針指向父結點，結果如下圖所示。

當前結點的關鍵字個數超過4，需要繼續分裂。左結點2個關鍵字，右結點2個關鍵字，關鍵字16進入到父結點中，將當前結點指向父結點，結果如下圖所示。

當前結點的關鍵字個數滿足條件，插入結束。

B+樹的刪除操作

如果葉子結點中沒有相應的key，則刪除失敗。否則執行下麵的步驟

1）刪除葉子結點中對應的key。刪除後若結點的key的個數大於等於Math.ceil(m-1)/2 – 1，刪除操作結束,否則執行第2步。

2）若兄弟結點key有富餘（大於Math.ceil(m-1)/2 – 1），向兄弟結點借一個記錄，同時用借到的key替換父結（指當前結點和兄弟結點共同的父結點）點中的key，刪除結束。否則執行第3步。

3）若兄弟結點中沒有富餘的key,則當前結點和兄弟結點合併成一個新的葉子結點，並刪除父結點中的key（父結點中的這個key兩邊的孩子指針就變成了一個指針，正好指向這個新的葉子結點），將當前結點指向父結點（必為索引結點），執行第4步（第4步以後的操作和B樹就完全一樣了，主要是為了更新索引結點）。

4）若索引結點的key的個數大於等於Math.ceil(m-1)/2 – 1，則刪除操作結束。否則執行第5步

5）若兄弟結點有富餘，父結點key下移，兄弟結點key上移，刪除結束。否則執行第6步

6）當前結點和兄弟結點及父結點下移key合併成一個新的結點。將當前結點指向父結點，重覆第4步。

註意，通過B+樹的刪除操作後，索引結點中存在的key，不一定在葉子結點中存在對應的記錄。

下麵是一顆5階B樹的刪除過程，5階B數的結點最少2個key，最多4個key。

a）初始狀態

b）刪除22,刪除後結果如下圖

刪除後葉子結點中key的個數大於等於2，刪除結束

c）刪除15，刪除後的結果如下圖所示

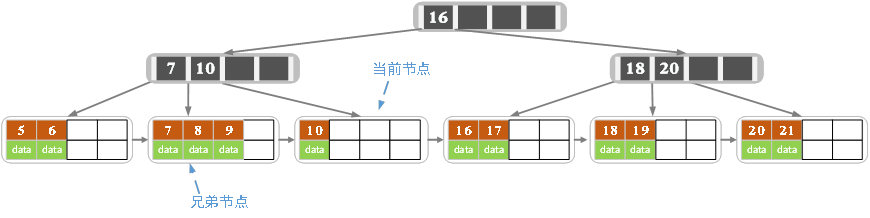
刪除後當前結點只有一個key,不滿足條件，而兄弟結點有三個key，可以從兄弟結點借一個關鍵字為9的記錄,同時更新將父結點中的關鍵字由10也變為9，刪除結束。

d）刪除7，刪除後的結果如下圖所示

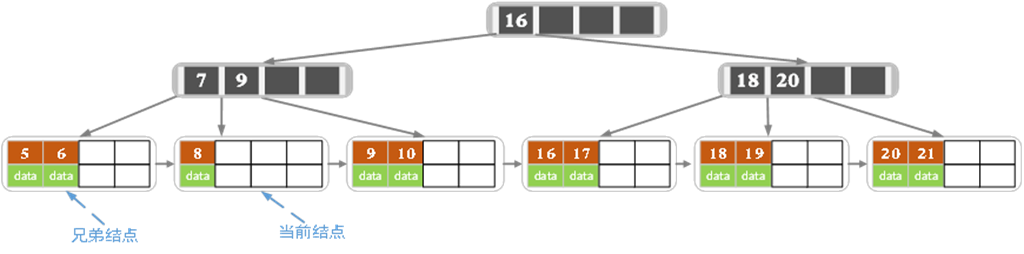
當前結點關鍵字個數小於2，（左）兄弟結點中的也沒有富餘的關鍵字（當前結點還有個右兄弟，不過選擇任意一個進行分析就可以了，這裡我們選擇了左邊的），所以當前結點和兄弟結點合併，並刪除父結點中的key，當前結點指向父結點。

此時當前結點的關鍵字個數小於2，兄弟結點的關鍵字也沒有富餘，所以父結點中的關鍵字下移，和兩個孩子結點合併，結果如下圖所示。

參考內容

[1] B+樹介紹

[2] 從MySQL Bug#67718淺談B+樹索引的分裂優化

[3] B+樹的幾點總結

沒看過癮?想要源文件?

由於微信公眾號篇幅限制有限,特在Gitee和Github開源了源文件 以及GitPage。如需查看完整HashMap解析或瞭解更多，請查看

開源項目《原理與源碼解析》, 另外掃描下方二維碼還可以領取技術棧圖譜哦~

本文由博客群發一文多發等運營工具平臺 OpenWrite 發佈