索引原理及B樹索引 http://hongyitong.github.io/2017/01/05/%E7%B4%A2%E5%BC%95%E5%8E%9F%E7%90%86%E5%8F%8AB%E6%A0%91%E7%B4%A2%E5%BC%95/ 一、索引的原理說白了，索引問題就是一個查找問題。數 ...

索引原理及B樹索引

http://hongyitong.github.io/2017/01/05/%E7%B4%A2%E5%BC%95%E5%8E%9F%E7%90%86%E5%8F%8AB%E6%A0%91%E7%B4%A2%E5%BC%95/

一、索引的原理

說白了，索引問題就是一個查找問題。資料庫索引，是資料庫管理系統中一個排序的數據結構，以協助快速查詢、更新資料庫表中數據。索引的實現通常使用B樹及其變種B+樹。在數據之外，資料庫系統還維護著滿足特定查找演算法的數據結構，這些數據結構以某種方式引用（指向）數據，這樣就可以在這些數據結構上實現高級查找演算法。這種數據結構，就是索引。
為表設置索引要付出代價的：一是增加了資料庫的存儲空間，二是在插入和修改數據時要花費較多的時間(因為索引也要隨之變動)。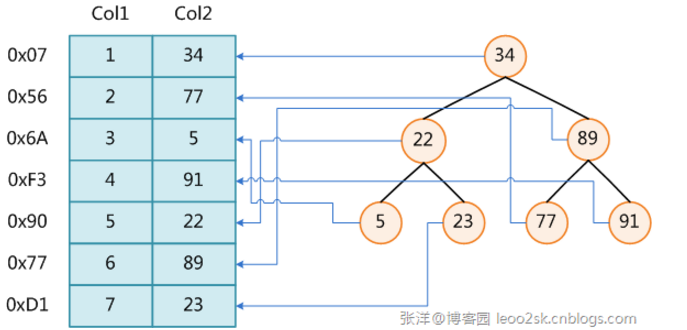

上圖展示了一種可能的索引方式。左邊是數據表，一共有兩列七條記錄，最左邊的是數據記錄的物理地址（註意邏輯上相鄰的記錄在磁碟上也並不是一定物理相鄰的）。為了加快Col2的查找，可以維護一個右邊所示的二叉查找樹，每個節點分別包含索引鍵值和一個指向對應數據記錄物理地址的指針，這樣就可以運用二叉查找在O( $\log_{2} n$

二、索引的優劣性

創建索引可以大大提高系統的性能。

第一，通過創建唯一性索引，可以保證資料庫表中每一行數據的唯一性。
第二，可以大大加快數據的檢索速度，這也是創建索引的最主要的原因。
第三，可以加速表和表之間的連接，特別是在實現數據的參考完整性方面特別有意義。
第四，在使用分組和排序子句進行數據檢索時，同樣可以顯著減少查詢中分組和排序的時間。
第五，通過使用索引，可以在查詢的過程中，使用優化隱藏器，提高系統的性能。

也許會有人要問：增加索引有如此多的優點，為什麼不對錶中的每一個列創建一個索引呢？因為，增加索引也有許多不利的方面。

第一，創建索引和維護索引要耗費時間，這種時間隨著數據量的增加而增加。
第二，索引需要占物理空間，除了數據表占數據空間之外，每一個索引還要占一定的物理空間，如果要建立聚簇索引，那麼需要的空間就會更大。
第三，當對錶中的數據進行增加、刪除和修改的時候，索引也要動態的維護，這樣就降低了數據的維護速度。

三、索引的原則

索引是建立在資料庫表中的某些列的上面。在創建索引的時候，應該考慮在哪些列上可以創建索引，在哪些列上不能創建索引。
一般來說，應該在這些列上創建索引：

在經常需要搜索的列上，可以加快搜索的速度；
在作為主鍵的列上，強制該列的唯一性和組織表中數據的排列結構；
在經常用在連接的列上，這些列主要是一些外鍵，可以加快連接的速度；
在經常需要根據範圍進行搜索的列上創建索引，因為索引已經排序，其指定的範圍是連續的；
在經常需要排序的列上創建索引，因為索引已經排序，這樣查詢可以利用索引的排序，加快排序查詢時間；
在經常使用在WHERE子句中的列上面創建索引，加快條件的判斷速度。

同樣，對於有些列不應該創建索引。
一般來說，不應該創建索引的的這些列具有下列特點：

第一，對於那些在查詢中很少使用或者參考的列不應該創建索引。這是因為，既然這些列很少使用到，因此有索引或者無索引，並不能提高查詢速度。相反，由於增加了索引，反而降低了系統的維護速度和增大了空間需求。
第二，對於那些只有很少數據值的列也不應該增加索引。這是因為，由於這些列的取值很少，例如人事表的性別列，在查詢的結果中，結果集的數據行占了表中數據行的很大比例，即需要在表中搜索的數據行的比例很大。增加索引，並不能明顯加快檢索速度。
第三，對於那些定義為text, image和bit數據類型的列不應該增加索引。這是因為，這些列的數據量要麼相當大，要麼取值很少。
第四，當修改性能遠遠大於檢索性能時，不應該創建索引。這是因為，修改性能和檢索性能是互相矛盾的。當增加索引時，會提高檢索性能，但是會降低修改性能。當減少索引時，會提高修改性能，降低檢索性能。因此，當修改性能遠遠大於檢索性能時，不應該創建索引。

四、索引的分類

根據資料庫的功能，可以在資料庫設計器中創建三種索引：唯一索引、主鍵索引和聚集索引。

1、唯一索引

唯一索引是不允許其中任何兩行具有相同索引值的索引。
當現有數據中存在重覆的鍵值時，大多數資料庫不允許將新創建的唯一索引與表一起保存。資料庫還可能防止添加將在表中創建重覆鍵值的新數據。例如，如果在employee表中職員的姓(lname)上創建了唯一索引，則任何兩個員工都不能同姓。

2、主鍵索引

資料庫表經常有一列或列組合，其值唯一標識表中的每一行。該列稱為表的主鍵。
在資料庫關係圖中為表定義主鍵將自動創建主鍵索引，主鍵索引是唯一索引的特定類型。該索引要求主鍵中的每個值都唯一。當在查詢中使用主鍵索引時，它還允許對數據的快速訪問。

3、聚集索引

在聚集索引中，表中行的物理順序與鍵值的邏輯（索引）順序相同。一個表只能包含一個聚集索引。
如果某索引不是聚集索引，則表中行的物理順序與鍵值的邏輯順序不匹配。與非聚集索引相比，聚集索引通常提供更快的數據訪問速度。
聚集索引對於任意給定的表而言是唯一的，一個表只能有一個聚集索引。不一定非要有聚集索引。聚集索引特殊的方面是：聚集索引的葉級是實際的數據-也就是說，數據重新排序，按照和聚集索引排序條件聲明的相同物理順序存儲。這意味著，一旦到達索引的葉級，就到達了數據。而非聚集索引，到達了葉級只是找到了數據的引用。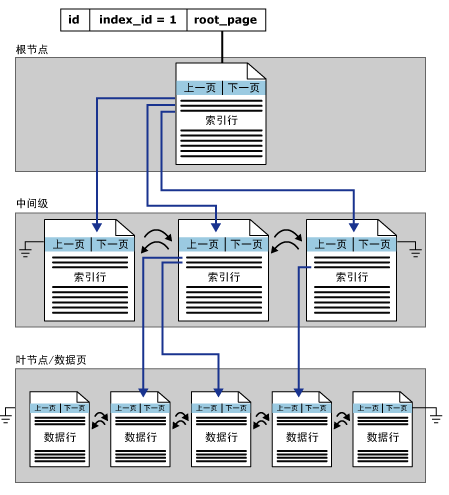

五、索引的效率

一般來說，索引本身也很大，不可能全部存儲在記憶體中，因此索引往往以索引文件的形式存儲的磁碟上。這樣的話，索引查找過程中就要產生磁碟I/O消耗，相對於記憶體存取，I/O存取的消耗要高幾個數量級，所以評價一個數據結構作為索引的優劣最重要的指標就是在查找過程中磁碟I/O操作次數的漸進複雜度。換句話說，索引的結構組織要儘量減少查找過程中磁碟I/O的存取次數。

1、B Tree

B樹（Balance Tree）又叫做B- 樹（其實B-是由B-tree翻譯過來，所以B-樹和B樹是一個概念），它就是一種平衡多路查找樹。下圖就是一個典型的B樹：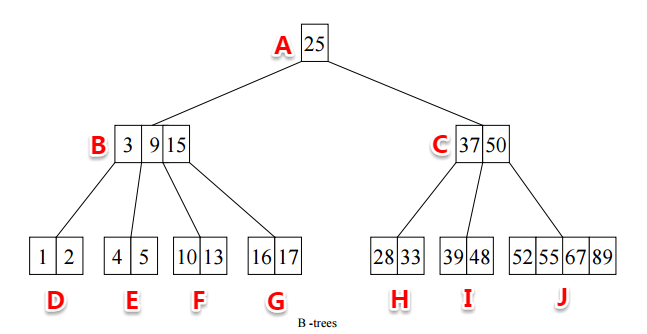

從上圖中我們可以大致看到B樹的一些特點，為了更好的描述B樹，我們定義記錄為一個二元組[key, data]，key為記錄的鍵值，data表示其它數據（上圖中只有key，沒有畫出data數據）。下麵是對B樹的一個詳細定義：

有一個根節點，根節點只有一個記錄和兩個孩子或者根節點為空；
每個節點記錄中的key和指針相互間隔，指針指向孩子節點；
d是表示樹的寬度，除葉子節點之外，其它每個節點有[d/2,d-1]條記錄，並且些記錄中的key都是從左到右按大小排列的，有[d/2+1,d]個孩子；
在一個節點中，第n個子樹中的所有key，小於這個節點中第n個key，大於第n-1個key，比如上圖中B節點的第2個子節點E中的所有key都小於B中的第2個key 9，大於第1個key 3;
所有的葉子節點必須在同一層次，也就是它們具有相同的深度；
由於B-Tree的特性，在B-Tree中按key檢索數據的演算法非常直觀：首先從根節點進行二分查找，如果找到則返回對應節點的data，否則對相應區間的指針指向的節點遞歸進行查找，直到找到節點或找到null指針，前者查找成功，後者查找失敗。

關於B-Tree有一系列有趣的性質，例如一個度為d的B-Tree，設其索引N個key，則其樹高h的上限為 $\log_{d} (N / 2)$

另外，由於插入刪除新的數據記錄會破壞B-Tree的性質，因此在插入刪除時，需要對樹進行一個分裂、合併、轉移等操作以保持B-Tree性質，本文不打算完整討論B-Tree這些內容，因為已經有許多資料詳細說明瞭B-Tree的數學性質及插入刪除演算法，有興趣的朋友可以查閱其它文獻進行詳細研究。

2、B+Tree

其實B-Tree有許多變種，其中最常見的是B+Tree，比如MySQL就普遍使用B+Tree實現其索引結構。B-Tree相比，B+Tree有以下不同點：

每個節點的指針上限為2d而不是2d+1；
內節點不存儲data，只存儲key；
葉子節點不存儲指針；
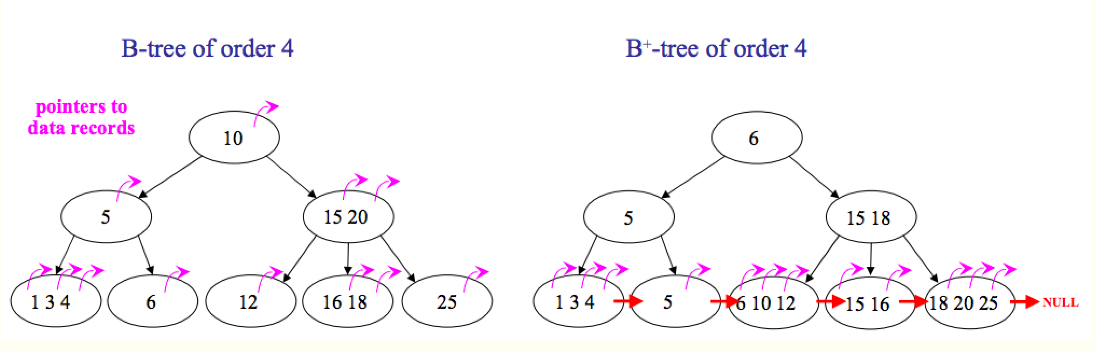
下麵是一個簡單的B+Tree示意。

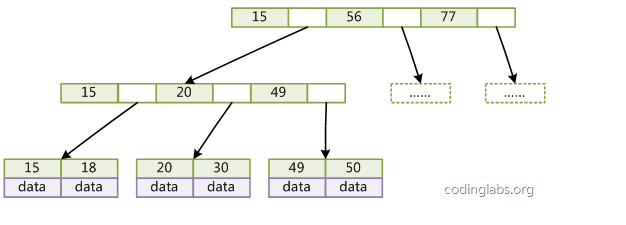
由於並不是所有節點都具有相同的域，因此B+Tree中葉節點和內節點一般大小不同。這點與B-Tree不同，雖然B-Tree中不同節點存放的key和指針可能數量不一致，但是每個節點的域和上限是一致的，所以在實現中B-Tree往往對每個節點申請同等大小的空間。一般來說，B+Tree比B-Tree更適合實現外存儲索引結構，具體原因與外存儲器原理及電腦存取原理有關，將在下麵討論。

帶有順序訪問指針的B+Tree：一般在資料庫系統或文件系統中使用的B+Tree結構都在經典B+Tree的基礎上進行了優化，增加了順序訪問指針。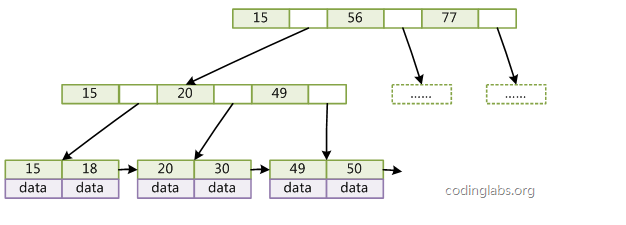

如圖所示，在B+Tree的每個葉子節點增加一個指向相鄰葉子節點的指針，就形成了帶有順序訪問指針的B+Tree。做這個優化的目的是為了提高區間訪問的性能，例如圖4中如果要查詢key為從18到49的所有數據記錄，當找到18後，只需順著節點和指針順序遍歷就可以一次性訪問到所有數據節點，極大提到了區間查詢效率。

2、B-樹和B+樹的比較

如圖所示，區別有以下兩點：

B+樹中只有葉子節點會帶有指向記錄的指針（ROWID），而B樹則所有節點都帶有，在內部節點出現的索引項不會再出現在葉子節點中。
B+樹中所有葉子節點都是通過指針連接在一起，而B樹不會。

B+樹的優點：

非葉子節點不會帶上ROWID，這樣，一個塊中可以容納更多的索引項，一是可以降低樹的高度。二是一個內部節點可以定位更多的葉子節點。
葉子節點之間通過指針來連接，範圍掃描將十分簡單，而對於B樹來說，則需要在葉子節點和內部節點不停的往返移動。

B樹的優點：

對於在內部節點的數據，可直接得到，不必根據葉子節點來定位。

六、B-樹和B+樹的效率分析

1、局部性原理與磁碟預讀

由於存儲介質的特性，磁碟本身存取就比主存慢很多，再加上機械運動耗費，磁碟的存取速度往往是主存的幾百分分之一，因此為了提高效率，要儘量減少磁碟I/O。為了達到這個目的，磁碟往往不是嚴格按需讀取，而是每次都會預讀，即使只需要一個位元組，磁碟也會從這個位置開始，順序向後讀取一定長度的數據放入記憶體。這樣做的理論依據是電腦科學中著名的局部性原理：當一個數據被用到時，其附近的數據也通常會馬上被使用。程式運行期間所需要的數據通常比較集中。
由於磁碟順序讀取的效率很高（不需要尋道時間，只需很少的旋轉時間），因此對於具有局部性的程式來說，預讀可以提高I/O效率。預讀的長度一般為頁（page）的整倍數。頁是電腦管理存儲器的邏輯塊，硬體及操作系統往往將主存和磁碟存儲區分割為連續的大小相等的塊，每個存儲塊稱為一頁（在許多操作系統中，頁得大小通常為4k），主存和磁碟以頁為單位交換數據。當程式要讀取的數據不在主存中時，會觸發一個缺頁異常，此時系統會向磁碟發出讀盤信號，磁碟會找到數據的起始位置並向後連續讀取一頁或幾頁載入記憶體中，然後異常返回，程式繼續運行。

2、B+樹性能分析

從上面介紹我們知道，B樹的搜索複雜度為O(h)=O( $\log_{d} N$

B+樹查找過程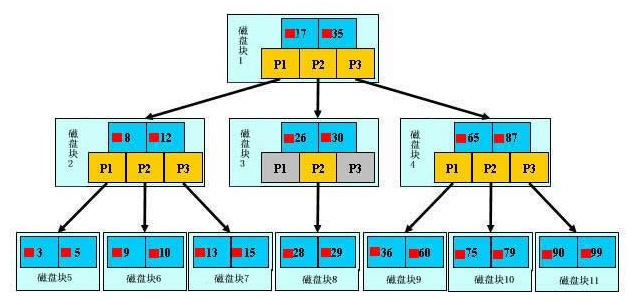

B-樹和B+樹查找過程基本一致。如上圖所示，如果要查找數據項29，那麼首先會把磁碟塊1由磁碟載入到記憶體，此時發生一次IO，在記憶體中用二分查找確定29在17和35之間，鎖定磁碟塊1的P2指針，記憶體時間因為非常短（相比磁碟的IO）可以忽略不計，通過磁碟塊1的P2指針的磁碟地址把磁碟塊3由磁碟載入到記憶體，發生第二次IO，29在26和30之間，鎖定磁碟塊3的P2指針，通過指針載入磁碟塊8到記憶體，發生第三次IO，同時記憶體中做二分查找找到29，結束查詢，總計三次IO。真實的情況是，3層的b+樹可以表示上百萬的數據，如果上百萬的數據查找只需要三次IO，性能提高將是巨大的，如果沒有索引，每個數據項都要發生一次IO，那麼總共需要百萬次的IO，顯然成本非常非常高。

# B+樹 # 索引 # 原理 # B樹