常見演算法

基礎演算法

目錄

• 基礎演算法
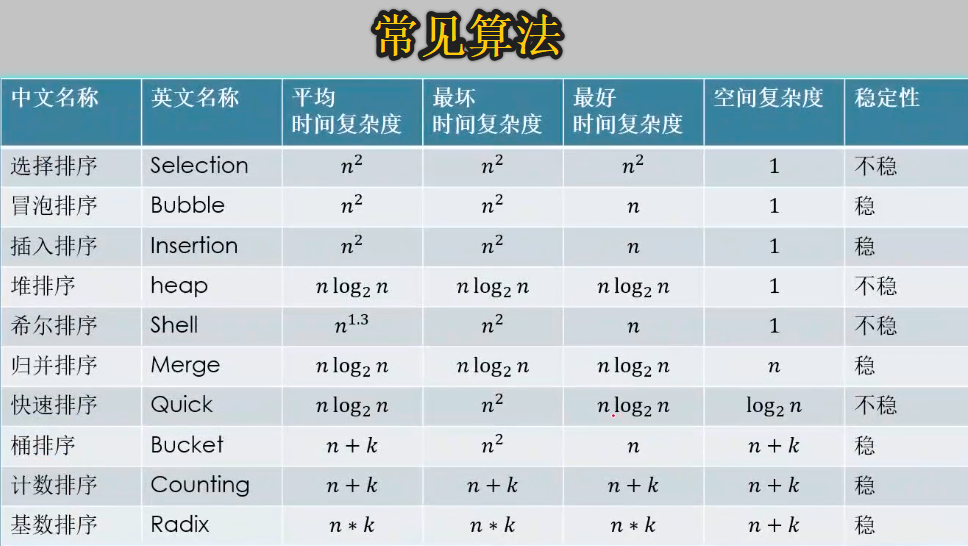
  • 演算法基礎
    • 演算法的定義和特征
    • 演算法設計的要求
    • 演算法的時間複雜度
    • 演算法空間複雜度
  • 排序二叉樹
  • 二分查找
  • 冒泡排序
  • 選擇排序
  • 插入排序
  • 希爾排序
  • 快速排序

演算法基礎

• 演算法的定義和特征

# 一個計算過程,解決問題的方法
- 解題方案的準確而完整的描述，是一系列解決問題的清晰指令，演算法代表著用系統的方法描述解決問題的策略機制,
能夠對一定規範的輸入，在有限時間內獲得所要求的輸出,如果一個演算法有缺陷，或不適合於某個問題，執行這個演算法
將不會解決這個問題,不同的演算法可能用不同的時間、空間或效率來完成同樣的任務。一個演算法的優劣可以用空間複雜度與時間複雜度來衡量.
# 特征
- 有窮性：演算法的有窮性是指演算法必須能在執行有限個步驟之後終止
- 確切性：演算法的每一步驟必須有確切的定義
- 輸入項：一個演算法有0個或多個輸入，以刻畫運算對象的初始情況，所謂0個輸入是指演算法本身定出了初始條件
- 輸出項：一個演算法有一個或多個輸出，以反映對輸入數據加工後的結果，沒有輸出的演算法是毫無意義的；
- 可行性：演算法中執行的任何計算步驟都是可以被分解為基本的可執行的操作步，即每個計算步都可以在有限時間內完成（也稱之為有效性）。

• 演算法設計的要求

- 確定性: 指的是演算法至少應該有輸入,輸出和加工處理無歧義性，能正確反映問題的需求,能夠得到問題的正確答案。
- 確定性大體分為四個層次:
    1.演算法程式無語法錯誤;
    2.演算法程式對於合法的輸入產生滿足要求的輸出;
    3.對於非法輸入能夠產生滿足規格的說明;
    4.演算法程式對於故意刁難的測試輸入都有滿足要求的輸出結果。

- 可讀性: 程式便於閱讀,理解交流。
- 健壯性: 當輸入數據不合法時,演算法也能作出相關處理，而不是產生異常,崩潰或者莫名其妙的結果。時間效率高和存儲量低

• 演算法的時間複雜度

# 定義
- 在進行演算法分析時，語句總的執行次數T(n)是關於問題規模n的函數，進而分析T(n)隨n的變化情況並確定T(n)的數量級.
- 演算法的時間複雜度，也就是演算法的時間量度，記作：T(n)=0(f(n))
- 它表示隨問題規模n的增大，演算法執行時間的埔長率和 f(n)的埔長率相同，稱作演算法的漸近時間複雜度，簡稱為時間複雜度。
其中f( n)是問題規橫n的某個函數.

# 求解演算法的時間複雜度的具體步驟
- 找出演算法中的基本語句 (演算法中執行次數最多的那條語句就是基本語句，通常是最內層迴圈的迴圈體)
- 計算基本語句的執行次數的數量級(只需計算基本語句執行次數的數量級，這就意味著只要保證基本語句執行次數的函數中的最高次冪正確即可，
可以忽略所有低次冪和最高次冪的繫數。這樣能夠簡化演算法分析，並且使註意力集中在最重要的一點上：增長率)
- 用大Ο記號表示演算法的時間性能(將基本語句執行次數的數量級放入大Ο記號中)

# 推導大o階的基本的推導方法：
- 用常數1取代運行時間中的所有加法常數。
- 在修改後的運行次數函數中，只保留最髙階項。
- 如果最高階項存在且不是1,則去除與這個項相乘的常數。簡單的說，就是保留求出次數的最高次冪，並且把繫數去掉。 如T(n)=n2+n+1 =O(n2)

#複雜度O(1) print("this is wd") 
#複雜度O(n) for i in range(n): print(i) 
#複雜度O(n2) for i in range(n): for j in range(n): print(j) 
#複雜度O(n3) for i in range(n): for j in range(n): for k in range(n): print('wd') 
#複雜度O(log2n) while n > 1: print(n) n = n // 2

#  常見的複雜度按效率排序：O(1)<O(logn)<O(n)<O(nlogn)<O(n2)<O(2nlogn)<O(n2) 

• 演算法空間複雜度

# 空間複雜度(Space Complexity)是對一個演算法在運行過程中臨時占用存儲空間大小的量度(三個方面)
- 包括存儲演算法本身所占用的存儲空間(存儲演算法本身所占用的存儲空間與演算法書寫的長短成正比，要壓縮這方面的存儲空間，就必須編寫出較短的演算法)
- 演算法的輸入輸出數據所占用的存儲空間(演算法的輸入輸出數據所占用的存儲空間是由要解決的問題決定的，
是通過參數表由調用函數傳遞而來的，它不隨本演算法的不同而改變)
- 演算法在運行過程中臨時占用的存儲空間(演算法在運行過程中臨時占用的存儲空間隨演算法的不同而異，有的演算法只
需要占用少量的臨時工作單元，而且不隨問題規模的大小而改變，這種演算法是節省存儲的演算法；有的演算法需要
占用的臨時工作單元數與解決問題的規模n有關，它隨著n的增大而增大，當n較大時，將占用較多的存儲單元)
- 具體表述
    1.當一個演算法的空間複雜度為一個常量，即不隨被處理數據量n的大小而改變時，可表示為O(1)；
    2.當一個演算法的空間複雜度與以2為底的n的對數成正比時，可表示為0(log2n)；
    3.當一個演算法的空間複雜度與n成線性比例關係時，可表示為0(n).若形參為數組，則只需要為它分配一個存儲由實
    4.參傳送來的一個地址指針的空間，即一個機器字長空間；若形參為引用方式，則也只需要為其分配存儲一個地
    5.址的空間，用它來存儲對應實參變數的地址，以便由系統自動引用實參變數。

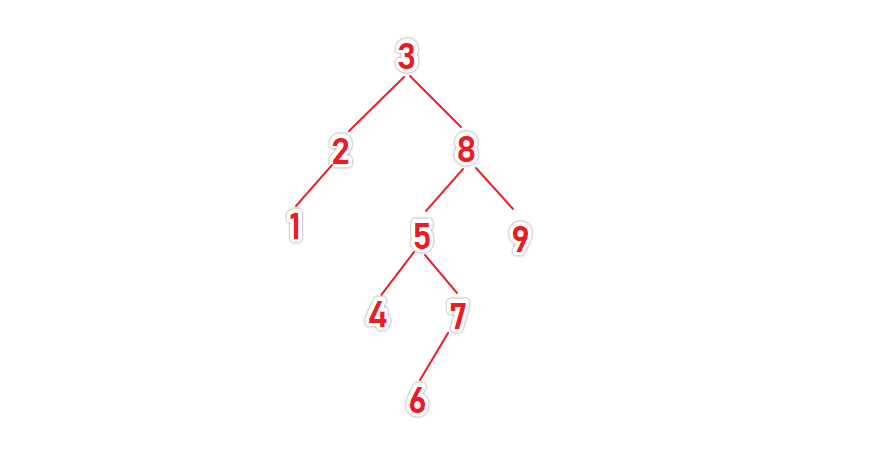
排序二叉樹

# 使用二叉樹 alist = [3,8,5,7,6,2,9,4,1] 進行排序
亂序數據的插入的時候，需要遵從一個準則：
- 插入的第一個數值作為樹的根節點
- 後序插入的數值，如果比根節點小，插入根節點的左側，否則插入到根節點的右側
- 使用深度優先中序遍歷

# 代碼
class Node():
    def __init__(self,item):
        self.item = item
        self.left = None
        self.right = None  
class SortTree():
    def __init__(self):
        self.root = None
    def add(self,item):
        node = Node(item)
        cur = self.root
        if self.root == None:
            self.root = node
            return
        while cur:
            #向右側插入
            if item > cur.item:
                if cur.right == None:
                    cur.right = node
                    break
                else:
                    cur = cur.right

            else:#向左插入
                if cur.left == None:
                    cur.left = node
                    break
                else:
                    cur = cur.left
                    
    def middle(self,root):#中序:左根右
        if root == None:
            return
        self.middle(root.left)
        print(root.item)
        self.middle(root.right)
        
tree = SortTree()
alist = [3,8,5,7,6,2,9,4,1]
for i in alist:
    tree.add(i)
tree.middle(tree.root)  
# 執行結果
1
2
3
4
5
6
7
8
9

二分查找

# 一定是基於有序集合的查找
- 有序列表對於我們的實現搜索是很有用的。在順序查找中，當我們與第一個元素進行比較時，
如果第一個元素不是我們要查找的，則最多還有 n-1 個元素需要進行比較。 二分查找則是從中間元素開始，
而不是按順序查找列表。 如果該元素是我們正在尋找的元素，我們就完成了查找。 如果它不是，我們可以
使用列表的有序性質來消除剩餘元素的一半。如果我們正在查找的元素大於中間元素，就可以消除中間元素
以及比中間元素小的一半元素。如果該元素在列表中，肯定在大的那半部分。然後我們可以用大的半部分重覆該過程，
繼續從中間元素開始，將其與我們正在尋找的內容進行比較。

# 二分查找原理
- 隨便想一個1～100的數字。
你的目標是以最少的次數猜到這個數字。你每次猜測後，我會說小了、大了或對了。
從50 開始,小了，但排除了一半的數字！至此，你知道1～50都小了。接下來，你猜75。大了，那餘下的數字又排除了一半！
使用二分查找時，你猜測的是中間的數字，從而每次都將餘下的數字排除一半。

#  需要搜索的元素越多,二分查找的速度比普通遍歷查找就快得多。
#  二分查找O(log n) 比普通遍歷查找O(n)時間複雜度低。

# 代碼
def find(alist,item):
    find = False
    first = 0
    last = len(alist)-1
    
    while first <= last:
        mid_index = (first + last) // 2
        
        if alist[mid_index] < item:#去中間元素的右側繼續去尋找
            first = mid_index + 1
        elif alist[mid_index] > item:
            last = mid_index - 1
        else:
            find = True
            break
    return find,mid_index

alist = [1,2,3,4,5,6,7,8,9]
print(find(alist,1))
# 執行結果
True

冒泡排序

# 原理
- 比較相鄰的元素。如果第一個比第二個大，就交換他們兩個。
- 對每一對相鄰元素做同樣的工作，從開始第一對到結尾的最後一對。在這一點，最後的元素應該會是最大的數。 
- 針對所有的元素重覆以上的步驟，除了最後一個。 
- 持續每次對越來越少的元素重覆上面的步驟，直到沒有任何一對數字需要比較。

# 代碼

#列表元素兩兩比較，大的值逐漸向後移動
def sort(alist):
    for i in range(len(alist)-1):
        if alist[i] > alist[i+1]:
            alist[i],alist[i+1] = alist[i+1],alist[i]
    return alist
alist = [3,8,5,7,6]
print(sort(alist))
# 執行結果 [3, 5, 7, 6, 8]

# 逐漸將亂序序列的最大值找出放置在亂序序列的尾部
def sort(alist):
    for j in range(len(alist)-1):
        for i in range(len(alist)-1-j):
            if alist[i] > alist[i+1]:
                alist[i],alist[i+1] = alist[i+1],alist[i]
    return alist

alist = [3,8,5,7,6]
print(sort(alist))   

# 執行結果 [3, 5, 6, 7, 8]

# 什麼時候最快
當輸入的數據已經是正序時（都已經是正序了，我還要你冒泡排序有何用啊）。

# 什麼時候最慢
當輸入的數據是反序時（寫一個 for 迴圈反序輸出數據不就行了，幹嘛要用你冒泡排序呢，我是閑的嗎）。

選擇排序

# 原理
- 選擇排序,可以理解為改進了冒泡排序，每次遍歷列表只做一次交換。為了做到這一點，一個選擇排序在他遍歷時尋找最大的值(最小值)，
併在完成遍歷後，將其放置在正確的位置(小的在前,大的在後)。直到所有元素均排序完畢。

# 代碼
# 將亂序中的最大值找出，跟最後一個元素交換位置
def sort(alist):
    max_index = 0 #最大值的下標
    for i in range(1,len(alist)):
        if alist[max_index] < alist[i]:
            max_index = i
    alist[len(alist)-1],alist[max_index] = alist[max_index],alist[len(alist)-1]
    return alist
# 執行結果 [3, 6, 5, 7, 8]

# 依次將亂序中的最大值找出，跟最後一個元素交換位置
def sort(alist):
    for j in range(0,len(alist)-1):
        max_index = 0 # 最大值的下標
        for i in range(1,len(alist)-j):
            if alist[max_index] < alist[i]:
                max_index = i
        alist[len(alist)-1-j],alist[max_index] = alist[max_index],alist[len(alist)-1-j]
    return alist

alist = [3,8,5,7,6]
print(sort(alist))
# 執行結果 [3, 5, 6, 7, 8]

# 選擇排序是一種簡單直觀的排序演算法，無論什麼數據進去都是 O(n²) 的時間複雜度。所以用到它的時候，
數據規模越小越好。唯一的好處可能就是不占用額外的記憶體空間了吧。

插入排序

# 原理
將第一待排序序列第一個元素看做一個有序序列，把第二個元素到最後一個元素當成是未排序序列。從頭到尾依次掃描未排序序列，
將掃描到的每個元素插入有序序列的適當位置。（如果待插入的元素與有序序列中的某個元素相等，則將待插入元素插入到相等元素的後面。）

# i有序子集中元素的個數,還可以表示下標
# alist[i]亂序子集中的第一個元素
# alist[i-1]有序子集中的最後一個元素

# 實現思路
i = 1 
if alist[i] < alist[i-1]:# 亂序子集中的第一個元素值小於有序子集中的最後一個元素的值,交換位置
    alist[i],alist[i-1] = alist[i-1],alist[i]
else:
    pass
i += 1

i = 2
while i > 0: # 有序子集個數大於0時,執行迴圈 
    if alist[i] < alist[i-1]: 
        alist[i],alist[i-1] = alist[i-1],alist[i]
        i -= 1
    else:
        break
        
# 完整代碼
def sort(alist):
    for i in range(1,len(alist)): # 控制遍歷次數,(len(alist)-1)就可以完成排序
        while i > 0:
            if alist[i] < alist[i-1]:
                alist[i],alist[i-1] = alist[i-1],alist[i]
                i -= 1
            else:
                break
    return alist

alist = [3,8,5,7,6]
print(sort(alist))

# 執行結果 [3, 5, 6, 7, 8]

希爾排序

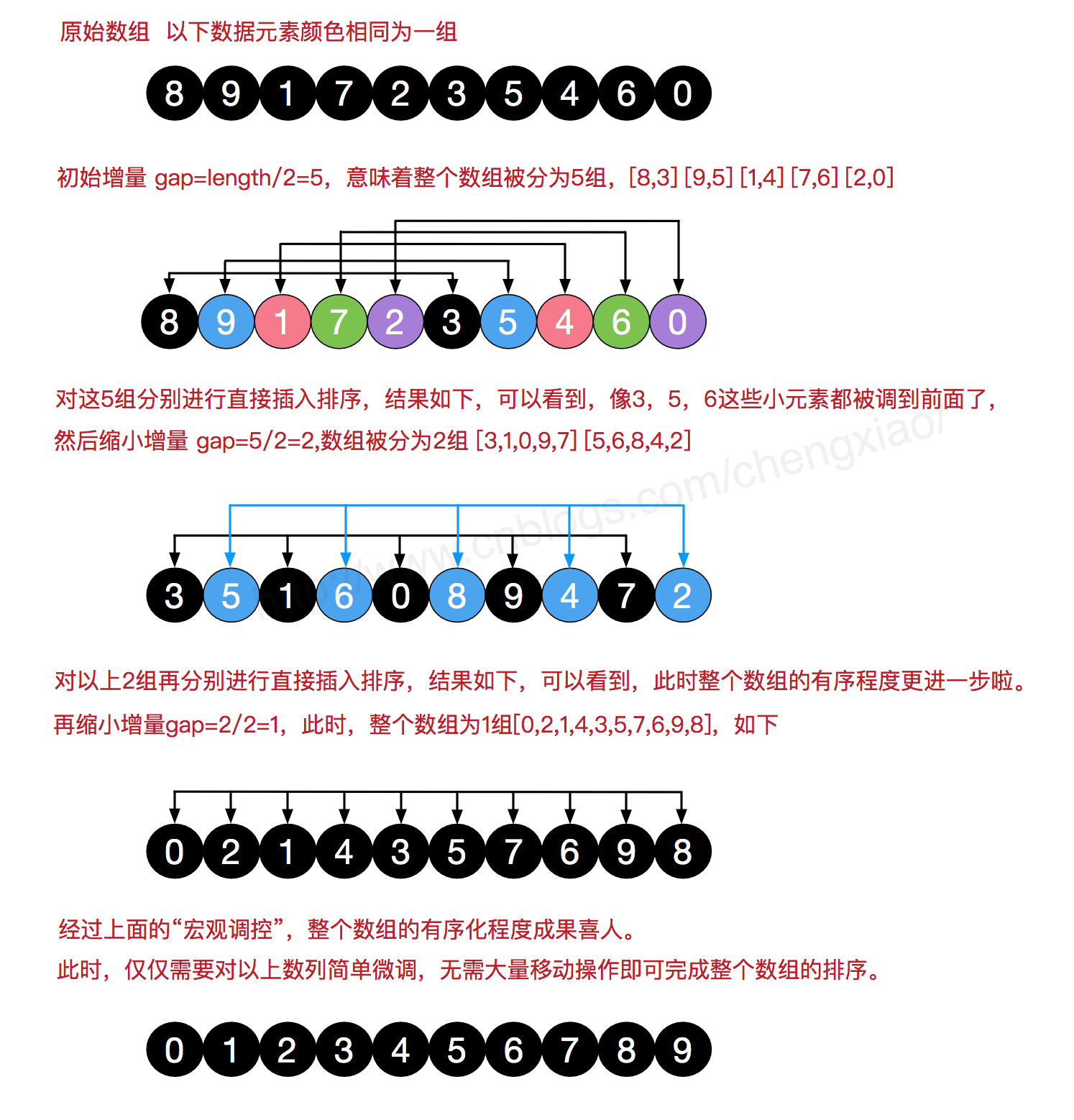
希爾排序(Shell Sort)是插入排序的一種。也稱縮小增量排序，是直接插入排序演算法的一種更高效的改進版本,
該方法的基本思想是：先將整個待排元素序列分割成若幹個子序列（由相隔某個“增量（gap）”的元素組成的）
分別進行直接插入排序，然後依次縮減增量再進行排序，待整個序列中的元素基本有序（增量足夠小）時，
再對全體元素進行一次直接插入排序。因為直接插入排序在元素基本有序的情況下（接近最好情況），效率是很高的，
因此希爾排序在時間效率比直接插入排序有較大提高。

希爾排序，也稱遞減增量排序演算法，是插入排序的一種更高效的改進版本。但希爾排序是非穩定排序演算法。
- 希爾排序是基於插入排序的以下兩點性質而提出改進方法的：
1.插入排序在對幾乎已經排好序的數據操作時，效率高，即可以達到線性排序的效率；
2.但插入排序一般來說是低效的，因為插入排序每次只能將數據移動一位；
  希爾排序的基本思想是：先將整個待排序的記錄序列分割成為若幹子序列分別進行直接插入排序，
待整個序列中的記錄"基本有序"時，再對全體記錄進行依次直接插入排序。    

# 代碼
def sort(alist):
    gap = len(alist)//2 #初始gap
    
    while gap >= 1:
        for i in range(gap,len(alist)):
            while i > 0:
                if alist[i] < alist[i-gap]:
                    alist[i],alist[i-gap] = alist[i-gap],alist[i]
                    i -= gap
                else:
                    break
        gap //= 2
    return alist
alist = [3,8,5,7,6]
print(sort(alist))
# 執行結果 [3, 5, 6, 7, 8]

快速排序

# 原理
1．先從數列中取出一個數作為基準數。
2．分區過程，將比這個數大的數全放到它的右邊，小於或等於它的數全放到它的左邊。
3．再對左右區間重覆第二步，直到各區間只有一個數。

# 實現流程
    - 將列表中第一個元素設定為基準數字，賦值給mid變數，然後將整個列表中比基準小的數值放在基準的左側，
比基準到的數字放在基準右側。然後將基準數字左右兩側的序列在根據此方法進行排放。
    - 定義兩個指針，low指向最左側，high指向最右側
    - 然後對最右側指針進行向左移動，移動法則是，如果指針指向的數值比基準小，則將指針指向的數字移動到基準數字原始的位置，
否則繼續移動指針。
    - 如果最右側指針指向的數值移動到基準位置時，開始移動最左側指針，將其向右移動，如果該指針指向的數值大於基準則將該數值
移動到最右側指針指向的位置，然後停止移動。
    - 如果左右側指針重覆則，將基準放入左右指針重覆的位置，則基準左側為比其小的數值，右側為比其大的數值。

def sort(alist,start,end):
    #基數
    low = start
    high = end 
    
    if low > high:
        return
    
    mid = alist[start]
    while low < high:
        #偏移high
        while low < high:
            if alist[high] >= mid:
                #向左偏移high
                high -= 1
            else:
                alist[low] = alist[high]
                break
        #偏移low
        while low < high:
            if alist[low] <= mid:
                low += 1
            else:
                alist[high] = alist[low]
                break
        if low == high:
            alist[low] = mid
            break
    #作用到左側
    sort(alist,start,high-1)
    #左右到右側
    sort(alist,low+1,end)
    return alist

alist = [6,1,2,7,9,3,4,5,10,6,1,8]
print(sort(alist,0,len(alist)-1))

# 執行結果
[1, 1, 2, 3, 4, 5, 6, 6, 7, 8, 9, 10]