45. 跳躍游戲 II 題目來源: "https://leetcode cn.com/problems/jump game ii" 題目 給定一個非負整數數組,你最初位於數組的第一個位置。 數組中的每個元素代表你在該位置可以跳躍的最大長度。 你的目標是使用最少的跳躍次數到達數組的最後一個位置。 示例 ...
45. 跳躍游戲 II
題目來源:https://leetcode-cn.com/problems/jump-game-ii
題目
給定一個非負整數數組,你最初位於數組的第一個位置。
數組中的每個元素代表你在該位置可以跳躍的最大長度。
你的目標是使用最少的跳躍次數到達數組的最後一個位置。
示例:
輸入: [2,3,1,1,4]
輸出: 2
解釋: 跳到最後一個位置的最小跳躍數是 2。
從下標為 0 跳到下標為 1 的位置,跳 1 步,然後跳 3 步到達數組的最後一個位置。
說明:
- 假設你總是可以到達數組的最後一個位置。
解題思路
思路:貪婪演算法
首先,先註意題意的說明部分【假設你總是可以到達數組的最後一個位置】。這裡只需要考慮,題目中所給出的數組,是一定能夠到達數組的最後一個位置。
這題要求與之前 55. 跳躍游戲 並不相同,55 題要求的返回是否能夠到達最後一個位置。如果用 55 題的反例來論證本題意義不大,若覺得有必要,也可以在無法到達時返回特定的值用以標記,例如 0。
現在考慮如何去求得到達最後位置的最小跳躍次數?
在這裡,我們考慮使用正向去找可到達的最遠位置。這裡以示例 1 為例,[2,3,1,1,4],索引為 0 的位置,這裡元素值為 2,表示該位置能夠跳躍到達的位置為後續兩個位置,如下圖所示紅色部分:
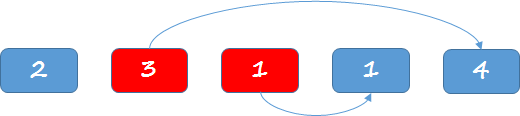
在這裡,索引為 1 的位置中,元素值值為 3,表示能夠後續三個位置,能到達最遠的位置為索引 4,這裡已經到達末尾位置。而索引 2 的位置中,值為 1,這裡只能跳躍到索引為 3 的位置。這裡顯然從索引 1 的位置跳躍能到達更遠的位置。
假設數組後續還未到達末尾,,現在選擇先跳到索引 1 的位置,上面說能夠在該位置能跳躍到後續三個位置,這裡如何選擇落腳的地方?跟上面討論的一樣,在每個可到達的位置,判斷各自能夠跳躍的最遠的位置。
現在位置在索引 1 的位置上面,如下圖所示,3 個紅色部分就是索引 1 這個位置能夠跳躍的選擇,而跳到索引 4 的位置,能夠跳躍更遠的位置,所以此處是當前最好的落腳點。

現在考慮如何實現?我們可以維護這個可到達的最遠位置,作為邊界。當我們正向遍歷的時候,當到達邊界時,就更新這個邊界,相應的跳躍次數加 1。
這裡需要註意一點,我們從正向遍歷的時候,不用遍歷最後一個位置。根據上面的說明知道,這裡一定會到達最後一個位置。那麼前面所述的需要維護的這個邊界,一定是大於或等於最後那個位置的。如果邊界剛好就在最後的位置時,按照前所述的到達邊界時,更新邊界,跳躍次數加 1 的邏輯,這裡會增加不必要的跳躍次數。所以不考慮訪問這個最後的位置。
具體的代碼實現如下。
代碼實現
class Solution:
def jump(self, nums: List[int]) -> int:
# 定義最遠位置,邊界,步數
max_pos = 0
end = 0
steps = 0
for i in range(len(nums) - 1):
# 獲取最遠可到達位置
max_pos = max(max_pos, i + nums[i])
# 到達邊界時,更新邊界
# 同時跳躍次數加 1
if i == end:
end = max_pos
steps += 1
return steps
實現結果
以上就是使用貪心演算法,從數組開始正向遍歷,維護可跳躍最遠的位置,確定邊界,到達邊界時,更新邊界,增加跳躍次數,進而解決《45. 跳躍游戲 II》問題的主要內容。
歡迎關註微信公眾號《書所集錄》



