線性SVM=線性分類器+最大間隔 間隔的形式化描述 SVM通過最大化`M`來求解參數`W`和`b`的,目標函數如下 拉格朗日乘數法, 軟間隔:加入容錯量 非線性SVM:特征空間。 常用的核函數 ...
SVM發展史

線性SVM=線性分類器+最大間隔
間隔(margin):邊界的活動範圍。The margin of a linear classifier is defined as the width that the boundary could be increased by before hitting a data point.
預備知識
- 線性分類器的分割平面(超平面):
Wx+b=0 - 點到超平面的距離:\(M=\frac{ \vert g(x) \vert }{\left\|W\right\| }\),其中\(g(x)=Wx+b\)
- SVM中正樣本定義為g(x)>=1,負樣本定義為g(x)<=-1
- SVM中Wx+b=1或者Wx+b=-1的點稱為支持向量
間隔的形式化描述
\(M=\frac{2}{\left\|W\right\| }\)
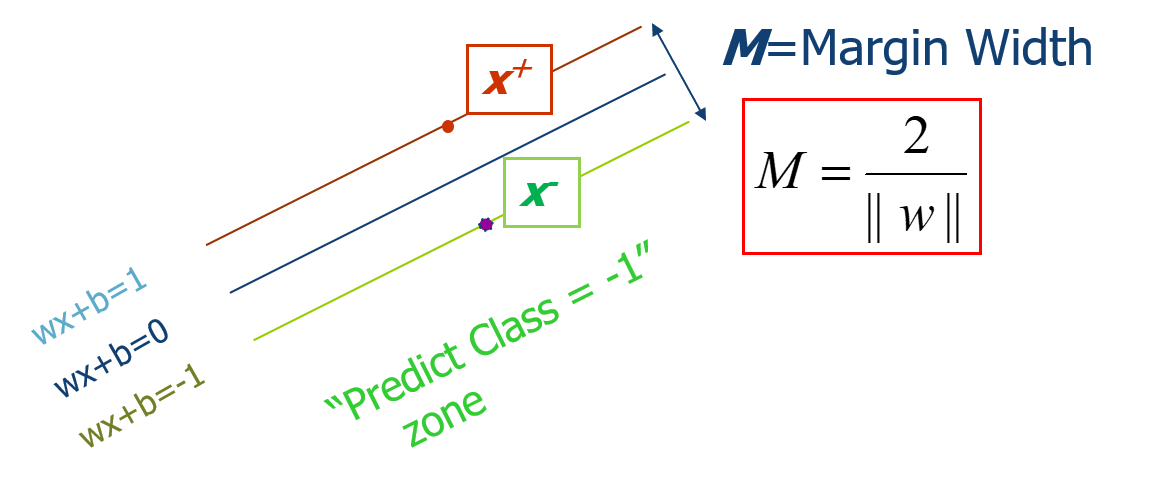
SVM通過最大化M來求解參數W和b的,目標函數如下:
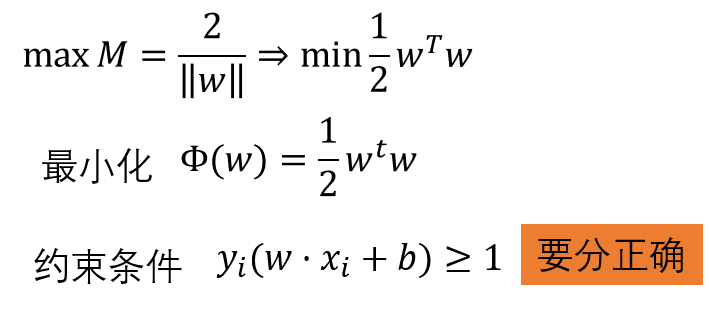
求解 :拉格朗日乘數法,偏導為0後回帶
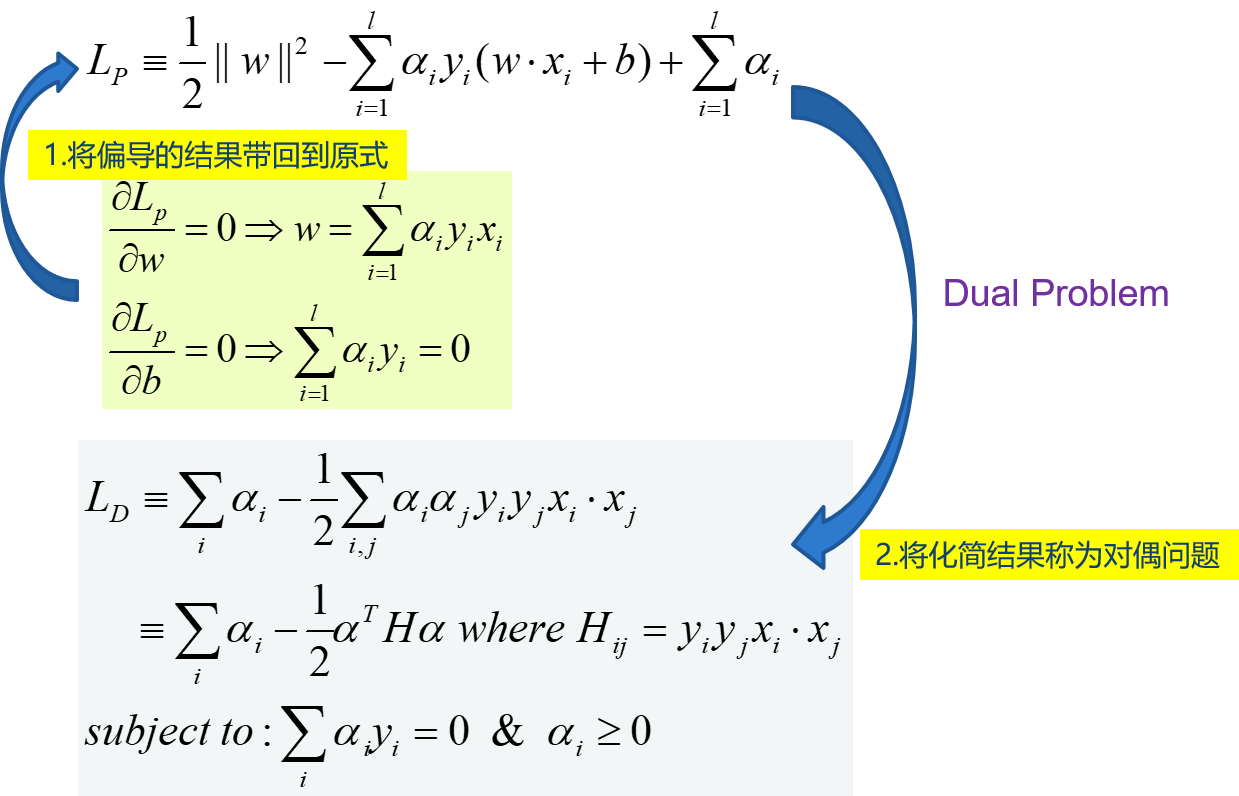
在SVM中,原問題和對偶問題具有相同的解,W已經求出:\(W=\sum_{i=1}^{l}{\alpha_iy_ix_i}\), 不等式約束,還需要滿足KKT條件。若\(\alpha_i>0\),則必有xi為支持向量,即:訓練完畢後,最終模型僅和支持向量有關。

b的求解過程如下

一個實例

軟間隔:加入容錯量
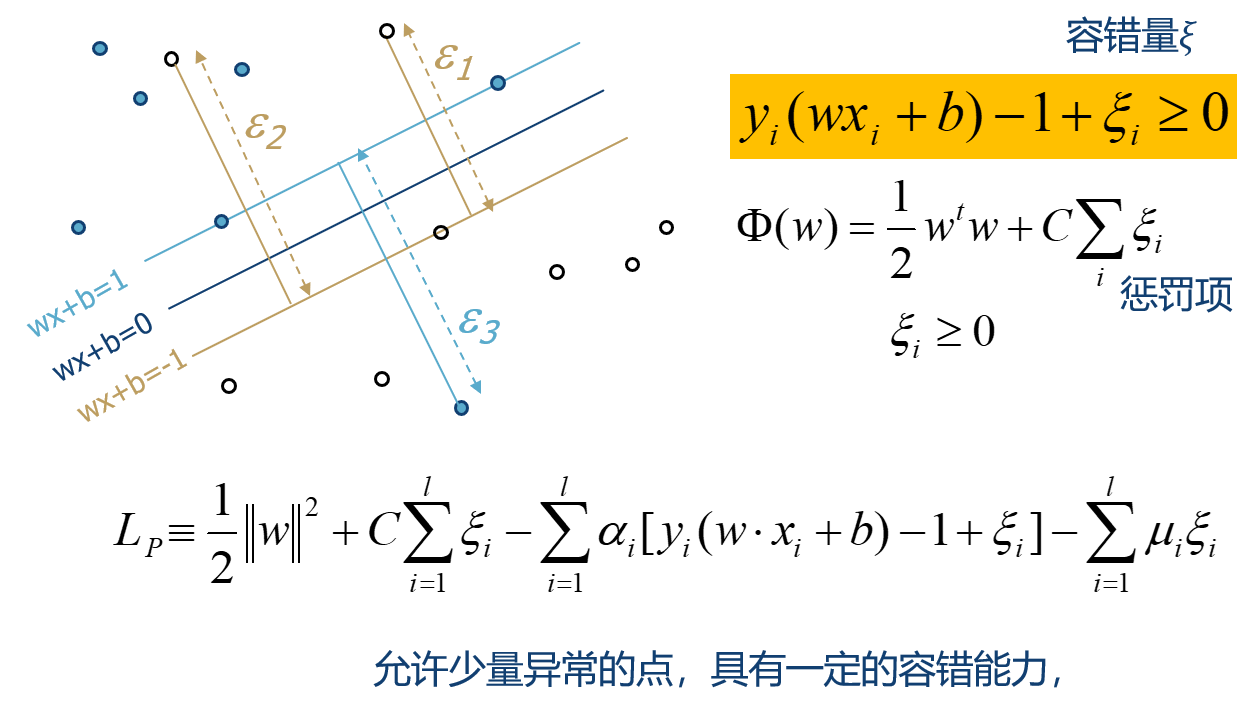
同樣採用拉格朗日乘數法求解
LD的區別僅僅體現為\(\alpha_i\)的約束不同。

非線性SVM:特征空間
通過映射到高維空間來將線性不可分的問題轉換為線性可分的問題。
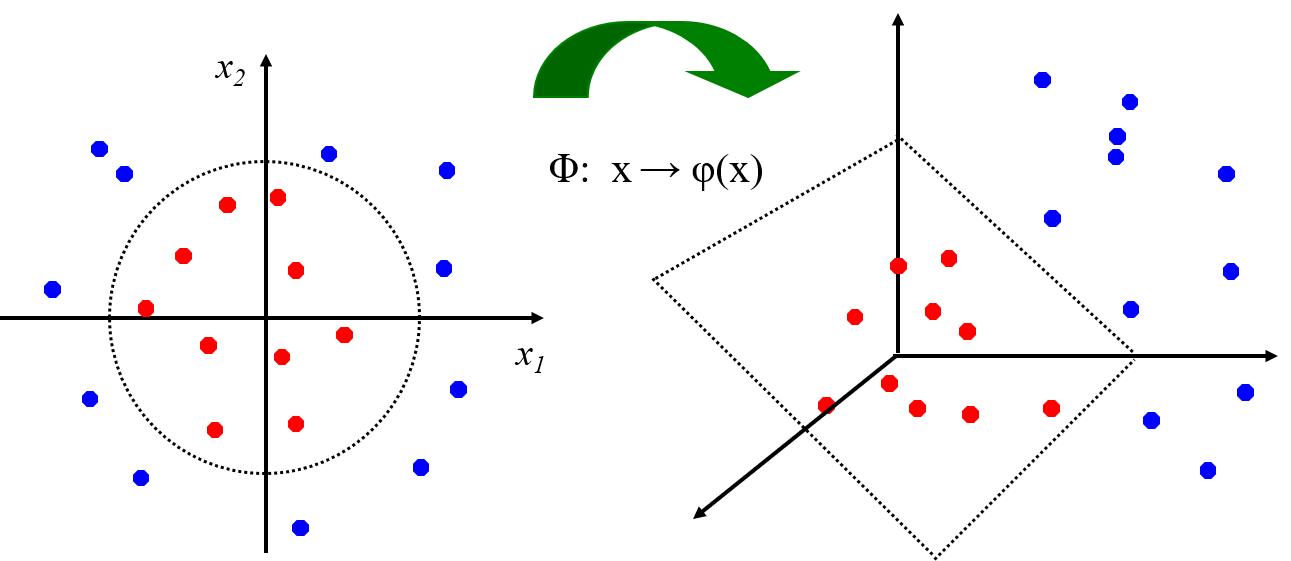
高維空間向量內積運算複雜度高。以二次型為例,直接計算
\(x_i⋅x_j⇒Φ(x_i)⋅Φ(x_j)\),直接計算的話,複雜度會成倍增加。
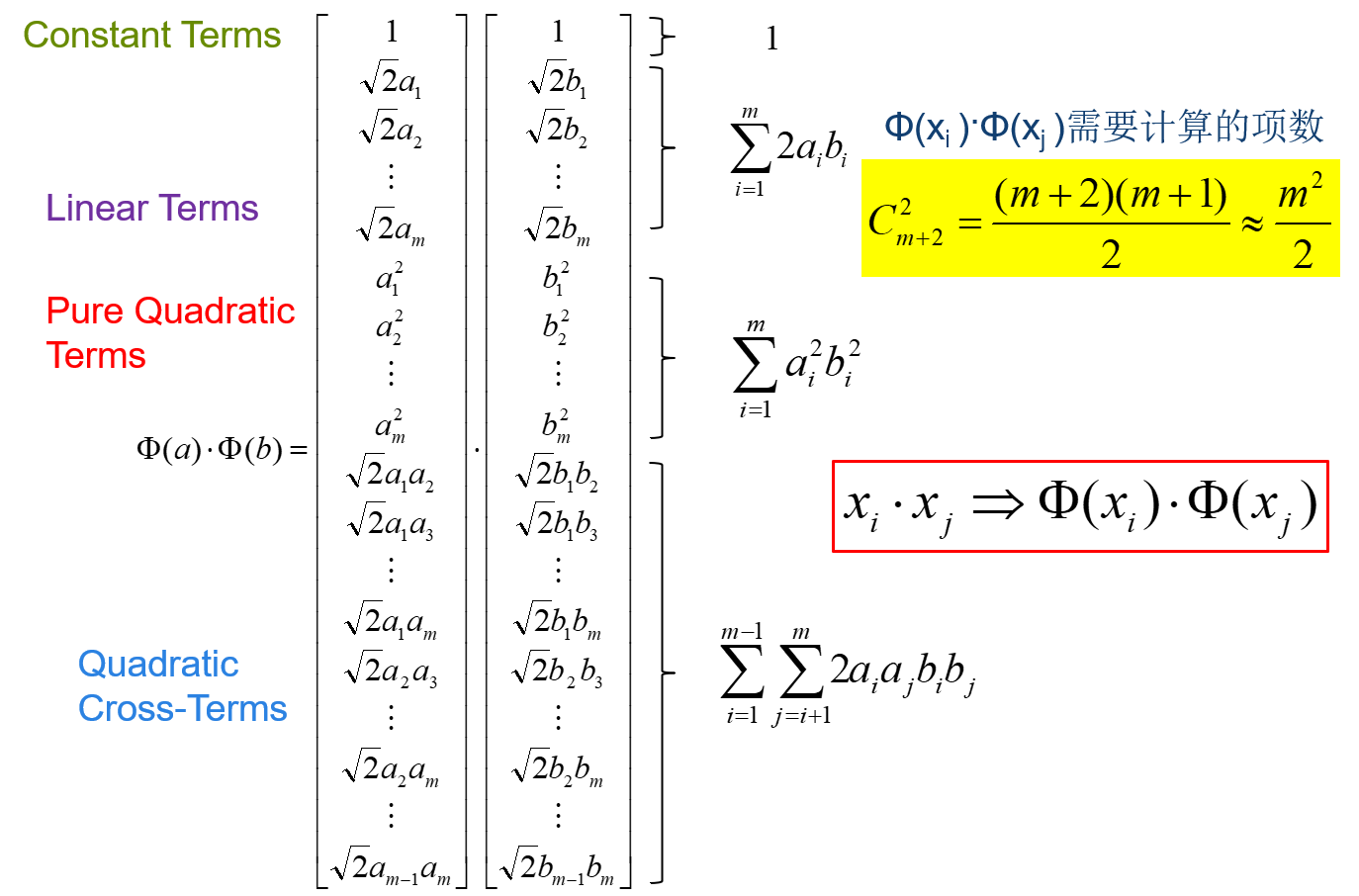
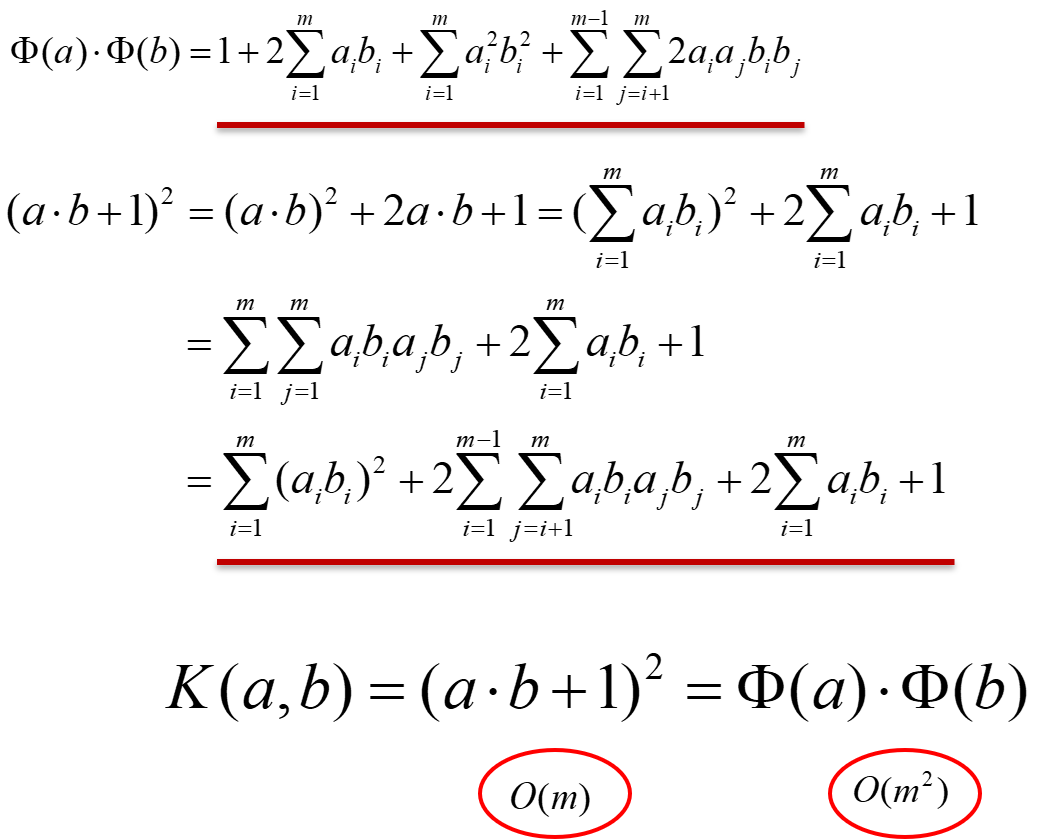
以二次型為例,理解核技巧
通過在低維空間的計算o(m),得到高維空間的結果,不需要知道變換是什麼,更不需要變換結果的內積,只需要知道核函數,就可以達到相同的目標。(變換結果的內積)
請看實例,二維空間
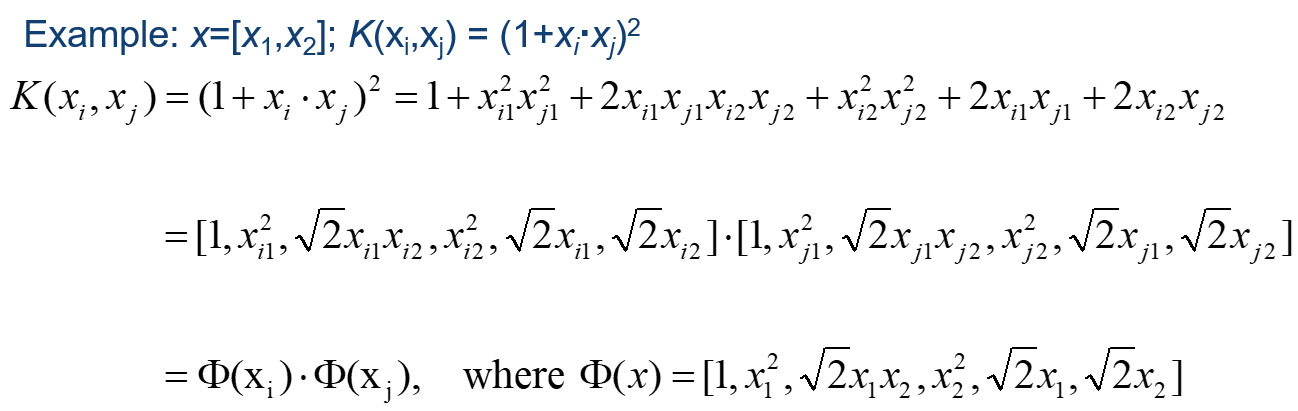
常用的核函數
多項式變換中,當d=2時,就是二次型變換。
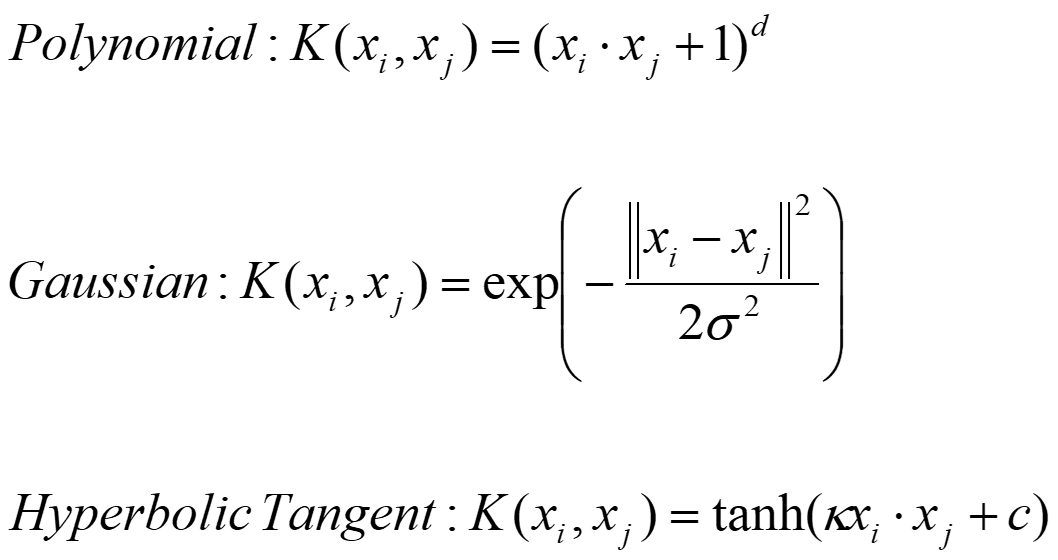
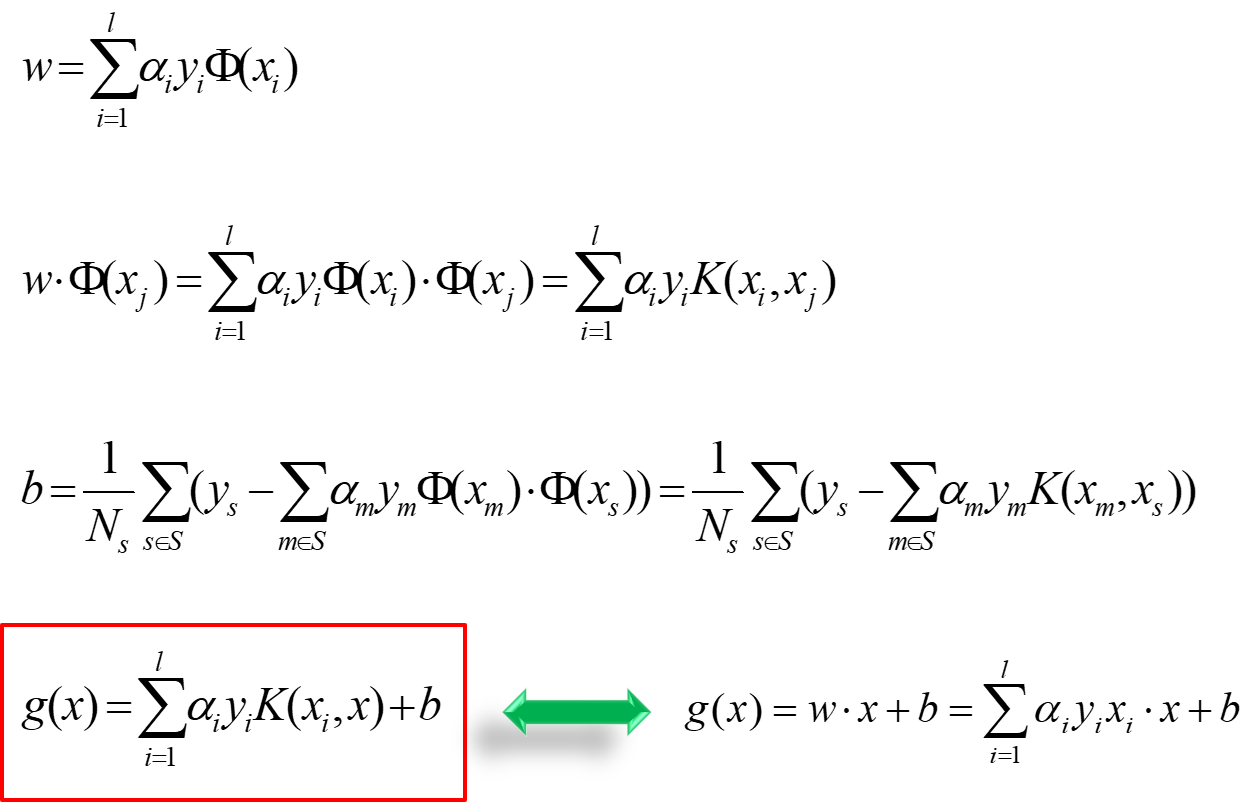
此時w和b的結果如下:
將\(x_i\)換為\(\phi(x_i)\),將\(\phi(x_i)\cdot \phi(x_j)\)換為\(K(x_i,x_j)\),其餘都不變,真的很簡潔。
SVM在Scikit-Learn中的應用
- Linear SVM:\(min\frac{1}{2}\left\|w\right\|^2+C\sum{\zeta^2}\)
LinearSVC(
penalty='l2',
C=1.0,#就是目標函數的C,C越大(eg:1e9),容錯空間越小,越接近硬邊界的SVM(最初的SVM,基本不用),C越小(eg:C=0.01),容錯空間越大,越接近soft Magin.
)
- 核函數 SVM:
from sklearn.svm import SVC
SVC(
C=1.0,
kernel='rbf',
degree=3,#多項式核函數的指數d
gamma='scale',#高斯基函數中的參數gamma,越大,函數分佈越狹窄; gamma越小,決策邊界越鬆弛,當很小時,可以認為趨於無窮大成一條直線了,這時就欠擬合了。gamma取值越大,決策邊界越收緊,當很小時,會無限包緊樣本點,這時就過擬合了。
)



