排序演算法之堆排序

目錄

• 排序演算法之堆排序
  • 什麼是堆?
  • 堆排序

什麼是堆?

• 堆是一顆完全二叉樹
• 堆分為 最大堆和最小堆
• 最大堆父節點都大於子節點, 最小堆父節點都小於子節點
• 左子節點: 2*i +1 (i: 父節點index)
• 右子節點: 2*i+2

堆排序

利用最大堆實現升序, 最小堆實現降序. 因為最大堆的根父節點一定是最大的, 讓它和隊尾元素互換, 然後在從堆中排除最後一個元素, 並複原最大堆. 迴圈 n-1次.

關鍵在於構建最大堆

最大堆的構建過程

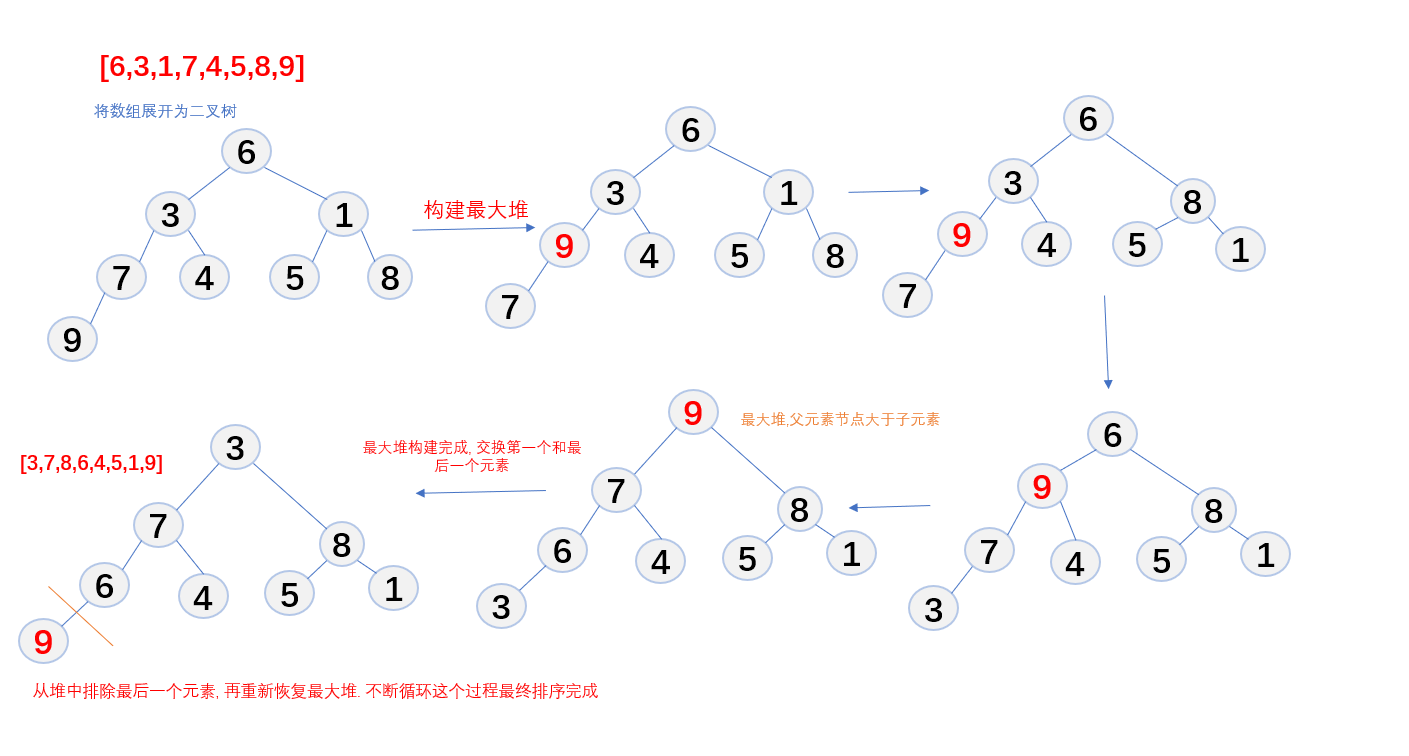
• 時間複雜度: O(n*log(n))
• 不穩定的排序
• 特征: 找出最大的元素放在末尾(升序)

    function heapSort(ary) {
        // 實現最大堆
        // start: 父節點, end: 迴圈深度
        function maxHeap(ary, start, end) {
            let parent = start, // 父節點
                son = parent*2 + 1, // 左子節點
                temp = null;
            // 規定循序最大深度
            while(son<=end) {
                // 如果存在右子節點, 並且判斷右節點是否大於左節點
                if(son+1<=end && ary[son] < ary[son+1]) son++;
                if(ary[son] > ary[parent]) {
                    temp = ary[son];
                    ary[son] = ary[parent];
                    ary[parent] = temp;
                    parent = son;
                    son = parent*2 +1;
                }else {
                    return;
                }
            }
        }
        // 構建最大堆  ary.length/2-1: 表示最後一個父節點
        for(let i = ary.length/2-1; i>=0; i--) {
            maxHeap(ary, i, ary.length-1);
        }
        // 排序
        for(let i = ary.length-1; i>0; i--) {
            let temp = ary[0];
            ary[0] = ary[i];
            ary[i]= temp;
            // 剔除最後一個元素,並複原最大堆
            maxHeap(ary, 0, i-1);
        }
        return ary;
    }

效果演示: