本篇博客主要詳細介紹朴素貝葉斯模型。首先貝葉斯分類器是一類分類演算法的總稱,這類演算法均以貝葉斯定理為基礎,故統稱為貝葉斯分類器。而朴素貝葉斯分類器是貝葉斯分類器中最簡單,也是最常見的一種分類方法。並且,朴素貝葉斯演算法仍然是流行的十大挖掘演算法之一,該演算法是有監督的學習演算法,解決的是分類問題。該演算法的優點 ...
本篇博客主要詳細介紹朴素貝葉斯模型。首先貝葉斯分類器是一類分類演算法的總稱,這類演算法均以貝葉斯定理為基礎,故統稱為貝葉斯分類器。而朴素貝葉斯分類器是貝葉斯分類器中最簡單,也是最常見的一種分類方法。並且,朴素貝葉斯演算法仍然是流行的十大挖掘演算法之一,該演算法是有監督的學習演算法,解決的是分類問題。該演算法的優點在於簡單易懂、學習效率高、在某些領域的分類問題中能夠與決策樹、神經網路相媲美。但由於該演算法以自變數之間的獨立(條件特征獨立)性和連續變數的正態性假設為前提(這個假設在實際應用中往往是不成立的),就會導致演算法精度在某種程度上受影響。
朴素貝葉斯法是基於貝葉斯定理與特征條件獨立假設的分類方法,是經典的機器學習演算法之一。最為廣泛的兩種分類模型是決策樹(Decision Tree Model)和朴素貝葉斯模型(Naive Bayesian Model,NBM)。和決策樹模型相比,朴素貝葉斯分類器(Naive Bayes Classifier 或 NBC)發源於古典數學理論,有著堅實的數學基礎,以及穩定的分類效率。同時,NBC模型所需估計的參數很少,對缺失數據不太敏感,演算法也比較簡單。理論上,NBC模型與其他分類方法相比具有最小的誤差率。
歷史背景解讀:
18世紀英國數學家托馬斯·貝葉斯(Thomas Bayes,1702~1761)提出過一種看似顯而易見的觀點:“用客觀的新信息更新我們最初關於某個事物的信念後,我們就會得到一個新的、改進了的信念。”這個研究成果由於簡單顯得平淡無奇,直至他死後兩年才於1763年由他的朋友理查德·普萊斯幫助發表。它的數學原理很容易理解,簡單說就是,如果你看到一個人總是做一些好事,則會推斷那個人多半會是一個好人。這就是說,當你不能準確知悉一個事物的本質時,你可以依靠與事物特定本質相關的事件出現的多少去判斷其本質屬性的概率。用數學語言表達就是:支持某項屬性的事件發生得愈多,則該屬性成立的可能性就愈大。與其他統計學方法不同,貝葉斯方法建立在主觀判斷的基礎上,你可以先估計一個值,然後根據客觀事實不斷修正。
1774年,法國數學家皮埃爾-西蒙·拉普拉斯(Pierre-Simon Laplace,1749-1827)獨立地再次發現了貝葉斯公式。拉普拉斯關心的問題是:當存在著大量數據,但數據又可能有各種各樣的錯誤和遺漏的時候,我們如何才能從中找到真實的規律。拉普拉斯研究了男孩和女孩的生育比例。有人觀察到,似乎男孩的出生數量比女孩更高。這一假說到底成立不成立呢? 拉普拉斯不斷地搜集新增的出生記錄,並用之推斷原有的概率是否準確。每一個新的記錄都減少了不確定性的範圍。拉普拉斯給出了我們現在所用的貝葉斯公式的表達:
該公式表示在B事件發生的條件下A事件發生的條件概率,等於A事件發生條件下B事件發生的條件概率乘以A事件的概率,再除以B事件發生的概率。公式中,P(A)也叫做先驗概率,P(A/B)叫做後驗概率。嚴格地講,貝葉斯公式至少應被稱為“貝葉斯-拉普拉斯公式”。
貝葉斯學派很古老,但是從誕生到一百年前一直不是主流。主流是頻率學派。頻率學派的權威皮爾遜和費歇爾都對貝葉斯學派不屑一顧,但是貝葉斯學派硬是憑藉在現代特定領域的出色應用表現為自己贏得了半壁江山。貝葉斯學派的思想可以概括為先驗概率+數據=後驗概率。也就是說我們在實際問題中需要得到的後驗概率,可以通過先驗概率和數據一起綜合得到。數據大家好理解,被頻率學派攻擊的是先驗概率,一般來說先驗概率就是我們對於數據所在領域的歷史經驗,但是這個經驗常常難以量化或者模型化,於是貝葉斯學派大膽的假設先驗分佈的模型,比如正態分佈,beta分佈等。這個假設一般沒有特定的依據,因此一直被頻率學派認為很荒謬。雖然難以從嚴密的數學邏輯里推出貝葉斯學派的邏輯,但是在很多實際應用中,貝葉斯理論很好用,比如垃圾郵件分類,文本分類。
概率基礎:
條件概率是指事件A在另外一個事件B已經發生條件下的發生概率。 條件概率表示為: P(A|B), 讀作“在B條件下A的概率”。若只有兩個事件A, B, 那麼:

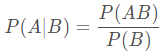
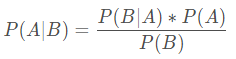
概念:
先驗概率:是指根據以往經驗和分析得到的概率。例如如果我們對西瓜的色澤、根蒂和紋理等特征一無所知,按照常理來說,西瓜是好瓜的概率是60%。那麼這個概率P(好瓜)就被稱為先驗概率。
後驗概率:事情已經發生,要求這件事情發生的原因是由某個因素引起的可能性的大小。例如假如我們瞭解到判斷西瓜是否好瓜的一個指標是紋理。一般來說,紋理清晰的西瓜是好瓜的概率大一些,大概是75%。如果把紋理清晰當作一種結果,然後去推測好瓜的概率,那麼這個概率P(好瓜|紋理清晰)就被稱為後驗概率。後驗概率類似於條件概率(紋理清晰的條件下是好瓜的概率)。
聯合概率:設二維離散型隨機變數(X,Y)所有可能取得值為,記則稱 為隨機變數X和Y的聯合概率。計算如下:
![]()
例:在買西瓜的案例中,P(好瓜,紋理清晰)稱為聯合分佈,它表示紋理清晰且是好瓜的概率。關於它的聯合概率,滿足以下乘法等式:
![]()
其中,P(好瓜|紋理清晰)就是後驗概率,表示在“紋理清晰”的條件下,是“好瓜”的概率。P(紋理清晰|好瓜)表示在“好瓜”的情況下,是“紋理清晰”的概率。
貝葉斯定理:
(註:P(x,c)=P(x│c)P(c))


後驗概率P(c∣x),在現實任務中通常難以直接獲得。所要實現的是基於有限的訓練樣本集儘可能準確地估計出後驗概率P(c│x)。有兩種策略:直接建模P(c∣x)來預測c,“判別式模型”;對聯合概率分佈P(x,c)P(x,c)P(x,c)建模,然後再由此獲得P(c|x),“生成式模型”。Fisher判別式、支持向量機等,都可歸入判別式模型的範疇。

對生成式模型(貝葉斯分類器):對於每個特征x,我們想要知道樣本在這個特性x下屬於哪個類別,即求後驗概率P(c|x)最大的類標記。這樣基於貝葉斯公式,可以得到:

P(c)是類“先驗”概率,P(x|c)是樣本x相對於類標記c的類條件概率,或稱似然。p(x)是用於歸一化的“證據”因數,對於給定樣本x,證據因數p(x)與類標記無關,即在下麵的示例中分母不做處理。於是,估計p(c|x)的問題變為基於訓練數據來估計先驗P(c)和似然P(x∣c),對於條件概率p(x|c)來說,它涉及x所有屬性的聯合概率。P(c)可通過各類樣本出現的頻率來進行估計。
逆概:(考慮事件)
貝葉斯分類器就是一種分類的方法,而且是一種基於貝葉斯原理,對聯合概率分佈p(x,c)建模,之後由條件概率公式得出後驗概率的生成式模型的方法 。因為後驗概率P(c∣x),在現實任務中通常難以直接獲得,所以朴素貝葉斯可以理解為求 "逆概" 。
例如:一座別墅在過去的 20 年裡一共發生過 2 次被盜,別墅的主人有一條狗,狗平均每周晚上叫 3 次,在盜賊入侵時狗叫的概率被估計為 0.9,問題是:在狗叫的時候發生入侵的概率是多少?
假設 A 事件為狗在晚上叫,B 為盜賊入侵。
事件A(狗叫):P(A) = 3/7
事件B(被偷):P(B) = 2/(365*20+4)
盜賊入侵時狗叫的概率被估計為 0.9(先偷後叫):P(A|B) = 0.9
考慮事件(反過來,逆概):P(B|A) = P(A|B) * P(B) / P(A) = 0.9* (2/(365*20+4)) / (3/7) = 0.000575
極大似然估計:
估計類條件概率的一種常用策略是先假定其具有某種確定的概率分佈形式,再基於訓練樣本對概率分佈的參數進行估計。
假設P(x∣c)具有確定的形式並且被參數向量θc唯一確定,則我們的任務就是利用訓練集D估計參數θc,我們將P(x|c)記為P(x∣θc)
參數估計有兩個學派:
1)頻率主義學派:認為參數雖然未知,但卻是客觀存在的固定值,可通過優化似然函數等準則來確定參數值。經典的方法:極大似然估計。
2)貝葉斯學派:認為參數是未觀察到的隨機變數, 可假定參數服從一個先驗分佈,然後基於觀測到的數據來計算參數的後驗分佈。
Dc表示訓練集D中第c類樣本組成的集合,假設這些樣本是獨立同分佈的,則參數θc對於數據集Dc的似然是:
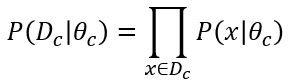
同時發生,因此連乘,對θc進行極大似然估計,就是去尋找能最大化似然P(Dc∣θc)的參數值θc,直觀上看,極大似然估計是試圖在θc所有可能的取值中,找到一個能使數據出現的“可能性”最大的值。
上式的連乘操作易造成下溢,通常使用對數似然:
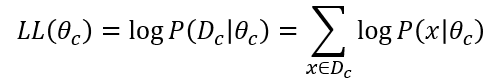
連乘轉換為連加,更好處理。此時參數θc 的極大似然估計為:

在連續屬性情形下,假設概率密度函數,則參數和的極大似然估計為:

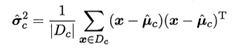
似然函數 L(x;θ)L(x;θ)L(x;θ)在形式上,其實就是樣本的聯合密度。把x1,x2,x3,…,xn看作常數,而把待定參數θ0,θ1,…,θn看作 L 的自變數。對連續型總體X 和離散型隨機變數X,樣本的似然函數分別是概率密度和分佈率的連乘形式。
朴素貝葉斯演算法:
是在貝葉斯演算法的基礎上進行了相應的簡化,即假定給定目標值時屬性之間相互條件獨立。也就是說沒有哪個屬性變數對於決策結果來說占有著較大的比重,也沒有哪個屬性變數對於決策結果占有著較小的比重。雖然這個簡化方式在一定程度上降低了貝葉斯分類演算法的分類效果,但是在實際的應用場景中,極大地簡化了貝葉斯方法的複雜性。在所有的機器學習分類演算法中,朴素貝葉斯和其他絕大多數的分類演算法都不同。對於大多數的分類演算法,比如決策樹,KNN,邏輯回歸,支持向量機等,他們都是判別方法,也就是直接學習出特征輸出Y和特征X之間的關係,要麼是決策函數Y=f(X),要麼是條件分佈P(Y|X)。但是朴素貝葉斯卻是生成方法,也就是直接找出特征輸出Y和特征X的聯合分佈P(X,Y),然後用P(Y|X)=P(X,Y)/P(X)得出。
基於貝葉斯公式來估計後驗概率P(c∣x)的主要困難:類條件概率P(x∣c)是所有屬性上的聯合概率,難以從有限的訓練樣本直接估計而得。朴素貝葉斯分類器採用了“屬性條件獨立性假設”:假設所有屬性相互獨立。基於屬性條件獨立性假設,貝葉斯公式可重寫為:
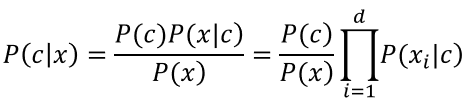
其中,d為屬性數目,xi為x在第i個屬性上的取值。由於對於所有的類別p(x)相同,即對於同一個樣本而言P(x)都是一樣的,對分類結果沒有什麼影響,為了提高運行效率,我們在計算時可以不考慮證據因數P(x)。最大化後驗概率便轉化為了最大化似然與先驗的乘積。基於上式的貝葉斯判定准則有:

這就是朴素貝葉斯分類器的表達式。朴素貝葉斯分類器的訓練過程就是基於訓練集D來估計類先驗概率P(c),併為每個屬性估計條件概率P(xi∣c)
類先驗概率:若Dc表示訓練集D中第c類樣本組成的集合,若有充足的獨立同分佈樣本,則可容易的估計出來類先驗概率
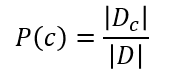
對於離散屬性而言,Dc,xi表示第c類第i個屬性上取值為xi的樣本,則條件概率P(xi∣c)可估計為:

對於連續屬性可考慮為概率密度函數,假定  分別是第c類樣本在第i個屬性上取值的均值和方差,則有:
分別是第c類樣本在第i個屬性上取值的均值和方差,則有:
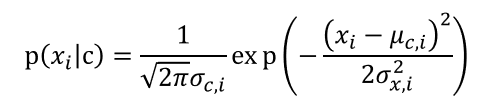
對於朴素貝葉斯還需要說明的一點是:若某種屬性值在訓練集中沒有與某個類同時出現過,則直接基於概率估計公式得出來概率為0,再通過各個屬性概率連乘式計算出的概率也為0,這就導致沒有辦法進行分類了,所以,為了避免屬性攜帶的信息被訓練集未出現的屬性值“抹去”,在估計概率值時通常要進行“平滑”,常用“拉普拉斯修正”,具體來講,令N表示訓練集D中可能的類別數,Ni表示第i個屬性可能的取值數。
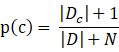

拉普拉斯修正避免了樣本不充分而導致概率估計為零的問題,並且在訓練集樣本變大的時候,修正過程所引入的先驗的影響也會逐漸變得可忽視,使得估計值越來越接近實際概率值。
案例分析1:
給定如下數據:
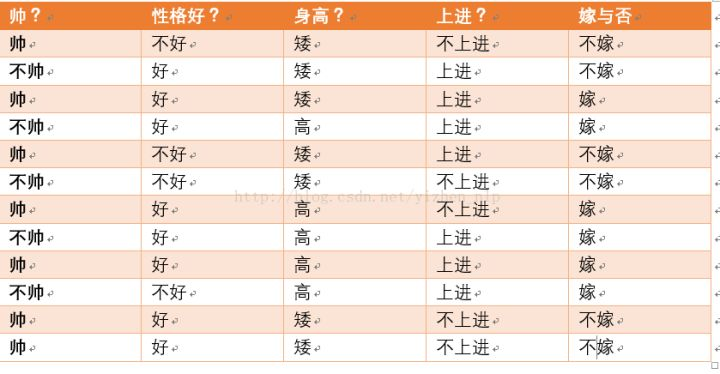
根據以上數據,現在有一對男女朋友,男生向女生求婚,男生的四個特點分別是不帥,性格不好,身高矮,不上進,請判斷女生是嫁還是不嫁?
該問題轉換為數學問題就是比較,該問題轉換為數學問題就是比較:P( 嫁 | 不帥,性格不好,身高矮,不上進 ) 與 P( 不嫁 | 不帥,性格不好,身高矮,不上進 ) 的概率。
由貝葉斯公式得:

假設各個特征相互獨立,即:
![]()
或者(其實沒區別):

首先我們整理訓練數據中:嫁的樣本數總共有6個,則 P(嫁) = 6 / 12 = 1 / 2;不帥,也嫁了的樣本數總共有6個,則 P(不帥 | 嫁) = 3 / 6 = 1 / 2; 性格不好,也嫁了的樣本數總共有1個,則 P(性格不好 | 嫁) = 1 / 6 ;身高矮,也嫁了的樣本數總共有1個,則 P(身高矮 | 嫁) = 1 / 6 ;不上進,也嫁了的樣本數總共有1個,則 P(不上進 | 嫁) = 1 / 6 ;

同理:
不嫁的樣本數總共有6個,則 P(不嫁) = 6 / 12 = 1 / 2;不帥,就不嫁的樣本數總共有1個,則 P(不帥 | 不嫁) = 1 / 6;性格不好,就不嫁的樣本數總共有3個,則P(性格不好 | 不嫁) = 3 / 6 = 1 / 2; 身高矮,就不嫁的樣本數總共有6個,則P(身高矮 | 不嫁) = 6 / 6 = 1;不上進,就不嫁的樣本數總共有3個,則P(不上進 | 不嫁) = 3 / 6 = 1 / 2;由於分母都相同,且分子(1 / 864) < (1 / 48) ,所以最後得出的結論是該女生不嫁給這個男生。
到此應該能整明白貝葉斯演算法是原理了,如果還沒整明白,沒關係,再來看一個例子。
案例解析2:
用西瓜數據集訓練一個朴素貝葉斯分類器,進行分類:
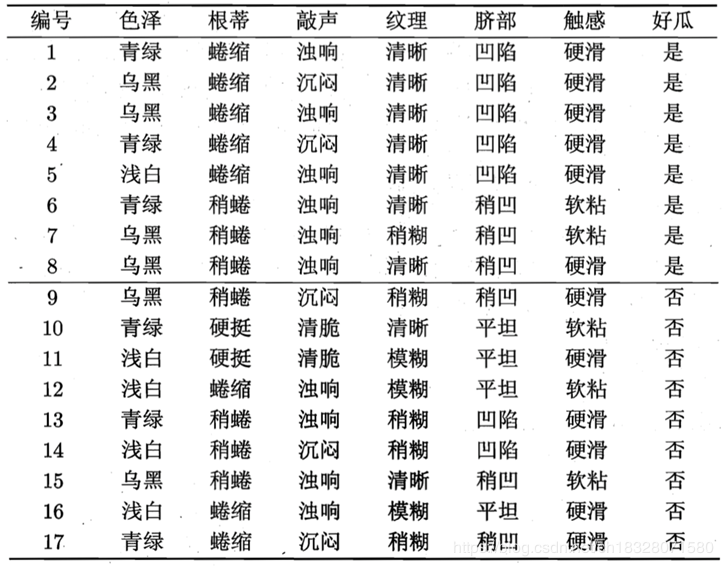
對下表示例進行預測:
1. 求出先驗概率P(c):
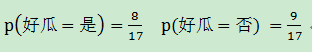
2. 求出每個屬性估計條件概率P(xi∣c):
離散屬性:

連續屬性:
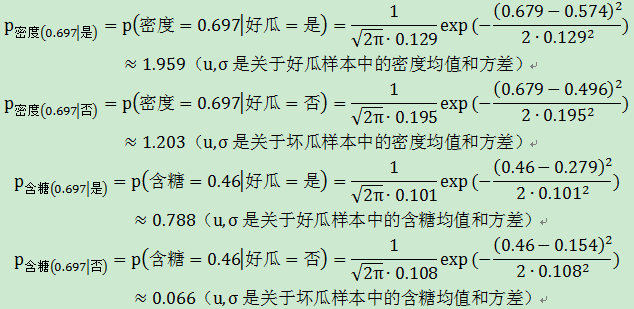
3. 最大化後驗概率,即計算先驗與類條件概率的乘積,數值大的對應的分類為分類結果。即採用朴素貝葉斯分類器的方法,假設各屬性之間相互獨立;不考慮證據因數P(x),轉化為: P(c∣x)=P(x∣c)P(c);最大化後驗概率便轉化為了最大化似然與先驗的乘積,maxP(x∣c)P(c)轉化為:



4. 預測結果,由計算結果可知,由於0.038>6.80×10−5,即P(好瓜=是)>P(好瓜=否),此瓜更有可能是好瓜,因此朴素貝葉斯分類器將測試樣本“測1”判別為“好瓜”。
5. 拉普拉斯修(補充)

朴素貝葉斯演算法實現原理總結:
貝葉斯分類器目的就是分類,即判斷含有屬性x的樣本屬於哪一類,也就是判斷後驗P(c│x)在不同的類別時概率的大小,後驗概率越大說明所屬的類別越有可能是正確的類別。因此,我們的目標就轉化為了最大化後驗概率,然後將後驗概率最大的類別判定為該樣本所屬的類別。例如:maxP(c∣x)=P(c2∣x)則x屬於c2。對於同一個樣本而言P(x)都是一樣的,對分類結果沒有什麼影響,為了提高運行效率,我們在計算時可以不考慮證據因數P(x)。最大化後驗概率便轉化為了最大化似然與先驗的乘積。則P(c∣x)=P(x∣c)P(c)/P(x) ,在不考慮P(x)後轉化為: P(c∣x)=P(x∣c)P(c)。
朴素貝葉斯的優缺點:
優點:
1. 對小規模的數據表現很好,適合多分類任務,適合增量式訓練,尤其是數據量超出記憶體時,我們可以一批批的去增量訓練;
2. 對缺失數據不太敏感,演算法也比較簡單,常用於文本分類;
3. 發源於古典數學理論,有著堅實的數學基礎,以及穩定的分類效率,當數據呈現不同的特點時,分類性能不會有太大的差異,健壯性好;
4. 當數據集屬性之間的關係相對比較獨立時,朴素貝葉斯分類演算法會有較好的效果。
缺點:
1. 對輸入數據的表達形式很敏感(離散、連續,值極大極小之類的);
2. 需要知道先驗概率,且先驗概率很多時候取決於假設,假設的模型可以有很多種,因此在某些時候會由於假設的先驗模型的原因導致預測效果不佳;
3. 由於我們是通過先驗和數據來決定後驗的概率從而決定分類,所以分類決策存在一定的錯誤率;
4. 理論上,朴素貝葉斯模型與其他分類方法相比具有最小的誤差率。但是實際上並非總是如此,這是因為朴素貝葉斯模型給定輸出類別的情況下,假設屬性之間相互獨立,這個假設在實際應用中往往是不成立的,在屬性個數比較多或者屬性之間相關性較大時,分類效果不好。而在屬性相關性較小時,朴素貝葉斯性能最為良好。對於這一點,有半朴素貝葉斯之類的演算法通過考慮部分關聯性適度改進。
補充:
1)半朴素貝葉斯分類器:(詳細內容待總結)在朴素的分類中, 我們假定了各個屬性之間的獨立,這是為了計算方便,防止過多的屬性之間的依賴導致的大量計算。這正是朴素的含義,雖然朴素貝葉斯的分類效果不錯,但是屬性之間畢竟是有關聯的, 某個屬性依賴於另外的屬性, 於是就有了半朴素貝葉斯分類器。
2)朴素貝葉斯與LR的區別?簡單來說:朴素貝葉斯是生成模型,根據已有樣本進行貝葉斯估計學習出先驗概率P(Y)和條件概率P(X|Y),進而求出聯合分佈概率P(XY),最後利用貝葉斯定理求解P(Y|X), 而LR是判別模型,根據極大化對數似然函數直接求出條件概率P(Y|X);朴素貝葉斯是基於很強的條件獨立假設(在已知分類Y的條件下,各個特征變數取值是相互獨立的),而LR則對此沒有要求;朴素貝葉斯適用於數據集少的情景,而LR適用於大規模數據集。
3)在估計條件概率P(X|Y)時出現概率為0的情況怎麼辦?簡單來說:引入λ,當λ=1時稱為拉普拉斯平滑。
4)一句話概況朴素貝斯:是一個生成模型(很重要),其次它通過學習已知樣本,計算出聯合概率,再求條件概率。
5)生成模式和判別模式的區別:生成模式:由數據學得聯合概率分佈,求出條件概率分佈P(Y|X)的預測模型;常見的生成模型有:朴素貝葉斯、隱馬爾可夫模型、高斯混合模型、文檔主題生成模型(LDA)、限制玻爾茲曼機。判別模式:由數據學得決策函數或條件概率分佈作為預測模型;常見的判別模型有:K近鄰、SVM、決策樹、感知機、線性判別分析(LDA)、線性回歸、傳統的神經網路、邏輯斯蒂回歸、boosting、條件隨機場。
參考文章:
1. https://blog.csdn.net/ch18328071580/article/details/94407134
2. https://blog.csdn.net/yangjingjing9/article/details/79986371
3. https://www.cnblogs.com/pinard/p/6069267.html
4. https://blog.csdn.net/sinat_30353259/article/details/80932111