*Preparation 1. Black's Futures Option Model (1) Key parameter: S = F, b = 0; (2) Task: Need an option for an asset (futures price = 120), assume K = ...
*Preparation

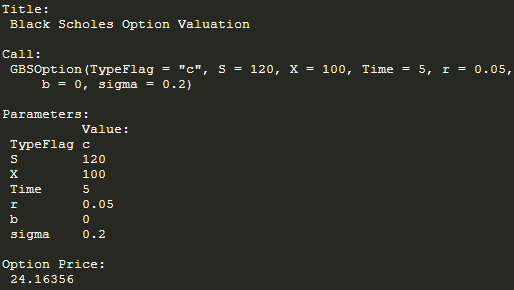
1. Black's Futures Option Model
(1) Key parameter: S = F, b = 0;
(2) Task: Need an option for an asset (futures price = 120), assume K = 100, T = 5, volatility = 20%, riskfree rate = 5%;
(3) Process and results:
GBSOption('c', 120, 100, 5, 0.05, 0, 0.2)
2. Pricing Cap Using Black
(1) Key parameter: S = F(n-1), b = 0;
(2) Notes:
Interest rate caps are interest rate derivatives, where holder receives positive payments throughout periods if interest rate exceeds certain level (strike price, K).
Interest rate floors the holder wins if interest rate below K.
(3) Task:
Need to pay USD LIBOR for 6 months to Alex between May and Nov 2020, so use caplet avoid interest rate risk.
Assume: the caplet on LIBOR rate with 2.5% strike price (i.e., if LIBOR > 2.5%, one period payoff = 0.5 * max[3% - 2.5%, 0]);
LIBOR follows Brownian Motion with 20% volatility;
forward rate between May and Nov = 2.2%;
spot rate = 2%;
(4) Process and results:
GBSOption('c', 0.022, 0.025, 0.5, 0.02, 0, 0.2)
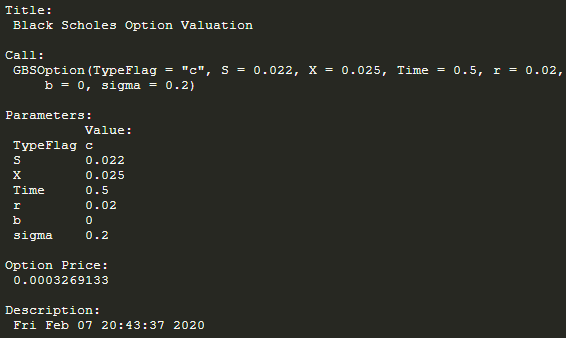
(5) VERY IMPORTANT!!!!!
Still need to multiply the time interval 0.5 on 0.0003269133 to get 0.0001634567, if unit is million USD, the final price of caplet will be 163USD;
Cap is sum of caplets !!! % LIBOR changes all the time, example above is just a single caplet calculation, below is whole method. Now assume that:
we need a cap that pays if LIBOR > 2.5% in first 3m, or if LIBOR > 2% in following 3m;
forward LIBOR rate in May~Aug is 2.1%, in Aug~Nov is 2.2%;
GBSOption('c', 0.021, 0.025, 0.25, 0.02, 0, 0.2) GBSOption('c', 0.022, 0.02, 0.25, 0.02, 0, 0.2)
# we seperately get two prices, each of them with time interval 0.25, so final price of cap is:
0.25 * (3.743394e-05 + 0.002179862)
0.000554324
# 3.743394e-05 is equivalent to 0.00003743394
PERFECT!!!!! So final price of cap will be 554USD.
3. Drawing Binomial Trees for Stock Option
(1) Key parameter: b = r;
(2) Assume:
Stock P0 = 900, K = 950, r = 2%, T = 3m, Volatility = 22%
(3) Process and results:
tree <- BinomialTreeOption(TypeFlag = 'ce', S = 900, X = 950, 1/4, 0.02, b = 0.02, sigma = 0.22, n = 3)
BinomialTreePlot(tree, dy = 1, xlab = 'Time steps', ylab = 'number of up steps', xlim = c(0, 4))
title(main = 'European Call Option')

(4) Comment:
This is CRR Binomial model, which converges to Black. Black Pricing is as below:
GBSOption('c', 900, 950, 1/4, 0.02, b = 0.02, sigma = 0.22)





