Day1 考的不是很好,T1T2沒區分度,T3想的太少,考試後期幾乎都是在摸魚,bitset亂搞也不敢打,只拿到了35分,跟前面的差距很大 A. 最大或 標簽: 二進位+貪心 題解: 首先x,y中一定有一個是R,考慮L的取值:對於每一位分為x中有沒有討論: 1>有 如果這一位不加以後全加可以>=L則 ...
Day1


考的不是很好,T1T2沒區分度,T3想的太少,考試後期幾乎都是在摸魚,bitset亂搞也不敢打,只拿到了35分,跟前面的差距很大
A. 最大或
標簽:
二進位+貪心
題解:
首先x,y中一定有一個是R,考慮L的取值:對於每一位分為x中有沒有討論:
1>有 如果這一位不加以後全加可以>=L則不選,否則選
2>沒有 如果這一位選上以後全不加也無法<=R則不選,否則選
因為位數從高到低枚舉,所以貪心是正確的
B. 答題
標簽:
折半搜索+二分
題解:
2<=n<=40,顯然是要折半搜索的,答案滿足單調性,可以二分判斷,check時複雜度最好是1<<20,而不是2e7的值域
說實話這道題比T1要簡單
C. 聯合權值·改
標簽:
啊啊啊起個標簽好藍啊
題解:
首先證明環的數量是$m*sqrt(m)$的:
考慮最壞情況:一定是一個競賽圖,那麼點數就是$sqrt(m)$,環數最多是$m*sqrt(m)$
有了這個性質下麵的演算法便有了複雜度保證:
1>對於第一問:
把每個點的出邊按w[to]降序排序,考慮枚舉$ x,y((x,y)\in{edge}),z((x,z)\in{edge}) $
只需要找到第一個不是三元環的z點便可以更新答案,複雜度與枚舉到的環有關,而每個環最多會被枚舉到3次,所以複雜度是對的
2>對於第二問:
考慮容斥:
用每個點的出點的權值和的平方減去平方的和,
再減去三元環的的情況,我是枚舉u,v用bitset求出b[u]&b[v].count()便是有u,v的三元環的個數
Day2
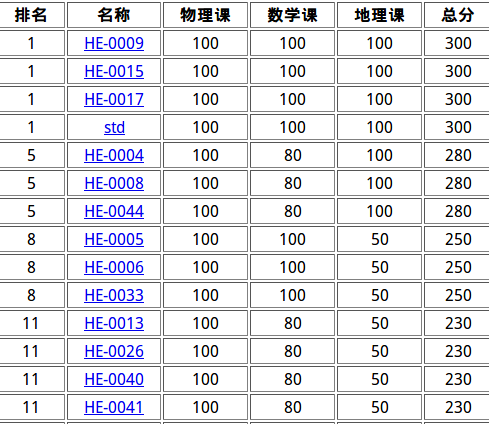

T1T2仍然沒區分度,T3原題沒看出來,總排rk10,翻盤失敗
A. 物理課
標簽:
物理?
題解:



