Cocos Creator 中 _worldMatrix 到底是什麼(上) 1. (矩陣)Matrix是什麼,有什麼用 (矩陣)Matrix一個神奇的存在?在開發過程中對裡邊各項值的含義是不是抓耳撓腮,百思不得其解?今天我們就來庖丁解牛,撥開它的神秘面紗。由於內容較多,關於Cocos Creator ...
Cocos Creator 中 _worldMatrix 到底是什麼(上)
1. (矩陣)Matrix是什麼,有什麼用
(矩陣)Matrix一個神奇的存在?在開發過程中對裡邊各項值的含義是不是抓耳撓腮,百思不得其解?今天我們就來庖丁解牛,撥開它的神秘面紗。由於內容較多,關於Cocos Creator 中的_worldMatrix會分為三篇文章完成。最終形成一個完整的demo
首先我們先看看在Cocos Creator編輯器中,對應圖形的變化都有那些屬性,如下圖
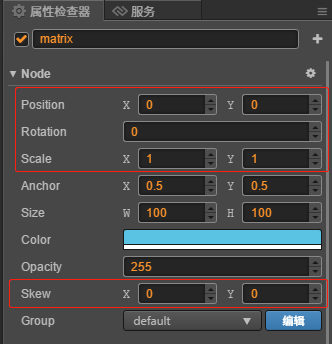
紅框的地方分別是位移、旋轉、縮放、傾斜它們都一一對應一個變換矩陣。
Cocos Creator 中的(矩陣)Matrix 是一個長度16的一維數組,按照先列後行的順序存儲一個 4 x 4 的放方陣。數組索引 0 1 2 3 分別表示矩陣第一列第1 2 3 4 行的數據。在2d的游戲坐標系中,一個三維矩陣就可以滿足基本的變換,但cocos creator 採用了四維矩陣,應該是為了和3d保持一致。矩陣表示如下(左邊體現Mat4對應屬性排列位置。右邊表示代碼中經常用到的變數a b c d tx ty與矩陣對應的位置信息)
$$
\left[
\begin{matrix}
m00&m04&m08&m12\
m01&m05&m09&m13\
m02&m06&m10&m14\
m03&m07&m11&m15\
\end{matrix}
\right]
=>
\left[
\begin{matrix}
a&c&0&0\
b&d&0&0\
0&0&1&0\
tx&ty&tz&1
\end{matrix}
\right]
$$
這樣的信息有什麼用呢?用來存儲節點 旋轉 縮放 傾斜 平移的圖形變換信息。要想知道其中緣由,複習一下線性代數及高數是很有必要的
- 矩陣乘法,以及相關性質
- 單位矩陣、逆矩陣、矩陣轉置
- 向量
- 齊次坐標
- 三角函數
有了以上知識,我們就可以簡單的推導下2d情況下,圖形變換對應的4中情況
2. 旋轉矩陣推導
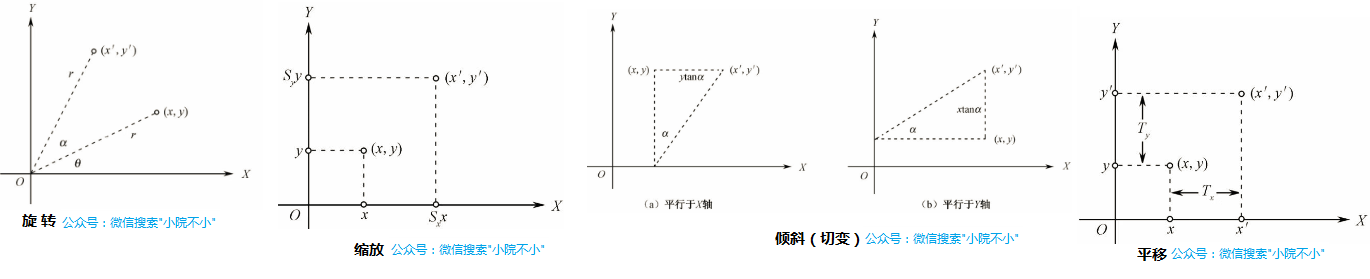
在2d坐標系中,假設存在點(x,y),我們將該點同原點(0,0)相連形成一個線段。此時線段與坐標系中x軸的弧度為a 。 我們將在以原點為圓心,線段的長度半徑r。逆時針旋轉弧度 b,該條線段另外一端坐標變為(x1,y1),如下圖(左1)
三個函數相關知識
- 正弦函數和餘弦函數
sin(a)=y/r => y = rsin(a)
cos(a)=x/r => x = rcos(a) - 和角公式
cos(a+b) = cos(a)cos(b) - sin(a)sin(b)
sin(a+b) = sin(a)cos(b) + cos(a)sin(b)
由三角函數可以推導出
x1 = rcos(a+b) = rcos(a)cos(b) - rsin(a)sin(b) = xcos(b) - ysin(b)
y1 = rsin(a+b) =rsin(a)cos(b) + rcos(a)sin(b) = ycos(b) + xsin(b) = xsin(b)+ysin(b)
轉換矩陣形式 B=AX
$$
\left[
\begin{matrix}
x1\y1\1
\end{matrix}
\right]
=
\left[
\begin{matrix}
cos(b)&-sin(b)&0\
sin(b)&cos(b)&0\
0&0&1
\end{matrix}
\right]
\times
\left[
\begin{matrix}
x\y\1
\end{matrix}
\right]
$$
在cocos creator中 ,採用行矩陣的寫法。以上在cocos creator實際運行形式如下,轉換公式如下 $B^T=X^T*A^T$。cocos creator 中剩下的縮放,傾斜,平移,請按照轉置矩陣,自行推導。
$$
\left[
\begin{matrix}
x1&y1&1
\end{matrix}
\right]
=
\left[
\begin{matrix}
x&y&1
\end{matrix}
\right]
\times
\left[
\begin{matrix}
cos(b)&sin(b)&1\
-sin(b)&cos(b)&1\
0&0&1
\end{matrix}
\right]
$$
3. 縮放矩陣推導
在2d坐標系中,假設存在點(x,y)縮放就是將坐標的x或y分別乘以一個縮放因數sx或sy。得到一個新的坐標(x1,y1),如下圖左2。

由此可得到縮放公式
x1=xsx = xsx + y0
y1=xsy = x0 + ysy
轉換矩陣形式 B=AX
$$
\left[
\begin{matrix}
x1\y1\1
\end{matrix}
\right]
=
\left[
\begin{matrix}
sx&0&0\
0&sy&0\
0&0&1
\end{matrix}
\right]
\times
\left[
\begin{matrix}
x\y\1
\end{matrix}
\right]
$$
4. 傾斜矩陣推導
在2d坐標系中,假設存在點(x,y)傾斜分為x軸傾斜以及y軸傾斜。沿x軸傾斜,就是將該點與點(x,0)連接而成的線段,以(x,0)為圓心,旋轉弧度a。如下圖(左3,左4) 得到一個新的坐標(x1,y1)。

由此可得到傾斜公式
- 沿x軸傾斜弧度a (圖左3)
x1=x+ytan(a)
y1=y
轉換矩陣形式 B=AX
$$
\left[
\begin{matrix}
x1\y1\1
\end{matrix}
\right]
=
\left[
\begin{matrix}
1&tan(a)&0\
0&1&0\
0&0&1
\end{matrix}
\right]
\times
\left[
\begin{matrix}
x\y\1
\end{matrix}
\right]
$$
- 沿y軸傾斜弧度a (圖左4)
x1=x
y1=y+xtan(a)=xtan(a)+y
轉換矩陣形式 B=AX
$$
\left[
\begin{matrix}
x1\y1\1
\end{matrix}
\right]
=
\left[
\begin{matrix}
1&0&0\
tan(a)&1&0\
0&0&1
\end{matrix}
\right]
\times
\left[
\begin{matrix}
x\y\1
\end{matrix}
\right]
$$
5. 平移矩陣推導
在2d坐標中,假設存在點(x,y)平移分別是將 x 或 y 加上 x方向位移 tx 或 y方向位移 ty。從而得到新的點坐標(x1,y1)(圖左5)

此可得到公式
x1=x+tx
y1=y+ty
轉換矩陣形式 B=AX
$$
\left[
\begin{matrix}
x1\y1\1
\end{matrix}
\right]
=
\left[
\begin{matrix}
1&0&tx\
0&1&ty\
0&0&1
\end{matrix}
\right]
\times
\left[
\begin{matrix}
x\y\1
\end{matrix}
\right]
$$
6. 複合變換
將變換矩陣,依次相乘得到一個新的矩陣記為$T_c$,使得$B=X*T_c$。所以**Cocos Creator中的,_worldMatrix,就是當前節點在世界坐標系中對應的複合變換矩陣**$T_c$。矩陣的乘法不滿足交換律。所以不同的順序,變換的效果會不相同。
7.小結
未完待續,中篇,我將分析CCNode.js 中 _updateLocalMatrix 方法為切入點,來加強對Cocos Creator 中 _worldMatrix理解。下篇,利用理解的知識完成圖形變換demo。再次加強對_worldMatrix認知。
歡迎感興趣的朋友關註我的微信訂閱號"小院不小",或者點擊下方的二維碼關註。我將多年開發中遇到的難點,以及一些有意思的功能,體會都會一一發佈到我的訂閱號中。需要本文demo可以在公眾號中回覆matrix

維護了一個Coscos Creator 的游戲開發群,歡迎喜歡聊技術的朋友加入

閑來無事,採用cocos creator開發了一個小游戲【坦克俠】,感興趣的朋友一個可以來玩玩




