每天兩題01

　　又是兩個月的時間過去了，上一次寫博客是7月14號，時間還是過的很快的，那麼問題來了，為什麼這麼長時間都沒有寫東西了呢？難道是在打醬油？

　　哈哈，說起來很慚愧，剛剛開始工作，碰到各種的問題要去學習要去解決，然後業餘的時間又去學了一些奇奇怪怪的東西，導致博客一直都落下了，歸根到底，還是自己懶惰了，因為心中總覺得今天又工作了一天，下班了要好好放鬆一下。不自覺的用這種心理在安慰自己，使得自己越來越放鬆了，然後又因為自己有點拖延症，想要寫點東西就一直拖著。。。

　　╮(￣▽￣")╭哎，話不多說了，最近源碼什麼的看的多了總覺得自己基礎還是不夠扎實，就想著業餘打打基礎，上班時間再看看框架寫寫業務邏輯什麼的應該比較好，每天打基礎的東西不多，就兩個題，貪多嚼不爛，題目選自劍指offer，有興趣的可以在github中自己看看哦，鏈接：https://github.com/CyC2018/CS-Notes

第一題：斐波那契數列

　　題目描述：大家都知道斐波那契數列，現在要求輸入一個整數n，請你輸出斐波那契數列的第n項。 n<=39

　　我的思路：什麼是斐波那契數列應該還是知道一點的，公式如上圖所示；簡單的來說就是從第三個數開始，任意一個數等於前面兩個數之和，比如0,1,1,2,3,5,8,13,22.......那麼最簡單的思路就是用遞歸，看下麵代碼：

public class Study01 {

    public static int feibo(int n){
        //要有下麵這兩個if，記住遞歸的話要有出口，然後會有死迴圈
        if (n==0) {
            return 0;
        }
        if (n==1 || n==2) {
            return 1;
        }
        return feibo(n-1)+feibo(n-2);
    }
    
    public static void main(String[] args) {
        
        int res = feibo(6);
        System.out.println(res);//8

    }
}

 　　上面的代碼寫出來了，但是可不可以優化一下，因為遞歸會導致一些值重覆的計算，例如計算feibo（5）=feibo（4）+feibo（3）=[ feibo（3）+ feibo（2）]  + feibo（3）,然後這裡電腦會計算兩次feibo（3），這裡電腦可不會像人一樣合併同類項然後計算啊，而一旦計算feibo（n），當n的值很大的時候，在遞歸計算過程中就會有很多的這種重覆計算的數，那麼我們有沒有辦法將這種重覆計算的數給剔除呢？只計算一次然後存起來，下一次再計算的話直接去拿就好了；

　　改進1：新建一個數組，我們從n=0開始，將每次算出來的數放到數組中，那麼數組中第n個位置的數就是我們需要的結果

//改進方式1
    public static int feiboUp01(int n){
        if (n==0) {
            return 0;
        }
        if (n==1 || n==2) {
            return 1;
        }
        int[] arr = new int[n+1];
        arr[0]=0;
        arr[1]=1;
        arr[2]=1;
        //這個迴圈每一次都會就算出來一個值填充到數組中，直到算出arr[n]
        for (int i = 3; i <= n; i++) {
            arr[i]=arr[i-1]+arr[i-2];
        }
        return arr[n];
    }
    
    public static void main(String[] args) {
        
        int res = feiboUp01(6);
        System.out.println(res);//8

    }

　　改進二：不知道有沒有發現上面這種做法雖然巧妙的利用了數組，但是對於我們來說，除了數組中的最後一個數，其他的數都是沒有什麼必要的，難道計算一個非常大的n，就要new一個這麼大的數組嗎？所以我們還可以繼續改進一下；

//改進方式2
    public static int feiboUp02(int n){
        if (n==0) {
            return 0;
        }
        if (n==1 || n==2) {
            return 1;
        }
        //這裡的三個變數，比如0,1,1,2,3,5，當current為5的時候，pre就是3，prepre就是2
        int prepre=1;
        int pre=1;
        int current = 0;
        //這裡有點不好理解，三個數prepre    pre    current
        //經過一次迴圈，計算current = prepre+pre，這個時候也要將prepre和pre往右移動一個位置，將
        //原來的pre指向現在的current，原來的prepre指向現在的pre
        for (int i = 3; i <= n; i++) {
            current = prepre+pre;
            prepre = pre;
            pre = current;
        }
        return current;
    }
    public static void main(String[] args) {
        
        int res = feiboUp02(6);
        System.out.println(res);

    }

 第二題：我們可以用 2x1 的小矩形橫著或者豎著去覆蓋更大的矩形。請問用 n 個 2x1 的小矩形無重疊地覆蓋一個 2xn 的大矩形，總共有多少種方法？

　　這個問題其實還是斐波那契數列，但是思路很有趣，一般我們想辦法計算有多少種方法的時候，可能就去畫圖計算去了，但是這裡卻是將一個大的問題拆成子問題，而子問題可以繼續拆...

　　如果n=1，只有一種情況，

　　如果n=2，只有兩種，兩塊都橫著或者兩塊都豎著

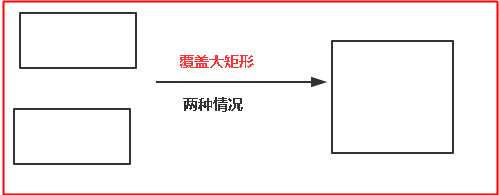
　　假如n=3，那麼問題就變成用 3個 2x1 的小矩形無重疊地覆蓋一個 2x3 的大矩形，第一種情況，填充的那一塊是橫著放的，如下所示，那麼剩下的需要填充的就是相當於n=2的情況，即2x2的情況；第二種情況就是第一塊填充的是豎著放的，那麼還需要再填充一塊，那麼剩下的就是n=1的情況；

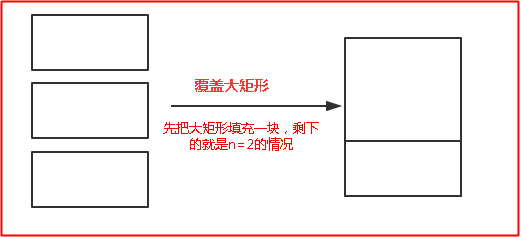
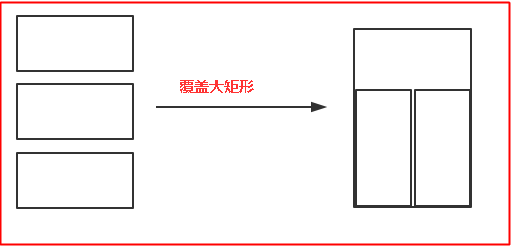
 　　依次類推，當n=5的時候也有兩種情況，第一種情況橫著填充一塊，剩下的就是n=4的那種；第二種情況豎著填充兩塊，剩下的就是相當於n=3的那種，通用公式如下，就不多說了，代碼的話和上面基本一樣，就不多說了。。。

 　　這兩個題目還是很有意思的，可以說一個題目是讓你看公式寫代碼，而另外一個題目其實用的是分治法，所謂的分治法，就是分而治之。就是將原問題劃分為n個規模較小，結構與原問題類似的小問題進行處理，遞歸地解決這些問題，然後再合併求解的過程。