註:這篇文章源於:https://mp.csdn.net/postedit/99710904, 無需懷疑抄襲,同一個作者,這是我在博客園的賬號。 在二叉樹中,有兩種非常重要的條件,分別是兩類數據結構的基礎性質。 其一是“堆性質”,二叉堆以及高級數據結構中的所有可合併堆都滿足“堆 性質”。 其二是 “ ...
註:這篇文章源於:https://mp.csdn.net/postedit/99710904, 無需懷疑抄襲,同一個作者,這是我在博客園的賬號。
在二叉樹中,有兩種非常重要的條件,分別是兩類數據結構的基礎性質。 其一是“堆性質”,二叉堆以及高級數據結構中的所有可合併堆都滿足“堆 性質”。 其二是 “BST性質”,它是二叉查找樹(Binary Search Tree)以及所有平衡樹的基礎。
二叉查找樹的定義
給定一棵二叉樹,樹上的每個節點都帶有一個數值,成為節點的 “關鍵碼” 。所謂BST性質是指,對於樹中的任意一個節點:
·該節點的關鍵碼不小於它的左子樹(如果非空)中任意節點的關鍵碼
·該節點的關鍵碼不大於它的右子樹(如果非空)中任意節點的關鍵碼 滿足上述性質的二叉樹就是一棵“二叉查找樹”(BST)。 二叉查找樹的中序遍歷是一個關鍵碼單調遞增的節點序列。
二叉查找樹的存儲
用數組模擬二叉樹
1 struct node { 2 int l, r;//左右子節點在數組中的下標 3 int val;//節點關鍵碼 4 }tree[Size];//數組模擬鏈表 5 int tot;//使用過和正在使用的節點總數量 6 int root;//當前根節點編號,即數組下標
優點:編程複雜度低。不需要考慮分配記憶體和回收記憶體
缺點:記憶體利用率低
用指針表示二叉樹
1 struct node { 2 node *l, *r; //指向左右兒子 3 int val;//節點關鍵碼 4 }root;
優點:記憶體利用率高
缺點:編程複雜度高
二叉查找樹的操作
BST支持的操作:
• 樹的建立
• 插入關鍵碼為x的節點
• 查詢關鍵碼為x的節點的排名
• 求關鍵碼為x的節點的前驅
• 求關鍵碼為x的節點的後繼
• 刪除關鍵碼為x的節點
二叉查找樹的建立
為了避免越界,減少邊界情況的特殊判斷,編程實現時一般在 BST中額外插入一個關鍵碼為正無窮和一個關鍵碼為負無窮的節點。 僅由這兩個節點構成的BST就是一棵初始的空BST。
int New(int val) { a[++tot].val = val; return tot; } void Build() { New(-INF), New(INF); root = 1, a[1].r = 2; }
二叉查找樹的檢索
在BST中檢索是否存在關鍵碼為val的節點。 設變數p等於根節點root,執行以下過程:
1.若p的關鍵碼等於val,則已經找到
2.若p的關鍵碼大於val
a.若p的左子節點為空,則說明不存在val
b.若p的左子節點不空,在p的左子樹中遞歸進行檢索
3.若瀃的關鍵碼小於val
a.若p的右子節點為空,則說明不存在val
b.若p的右子節點不空,在p的右子樹中遞歸進行檢索
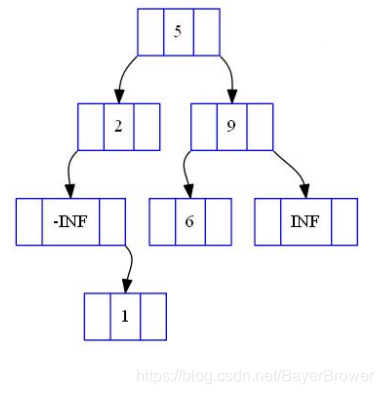
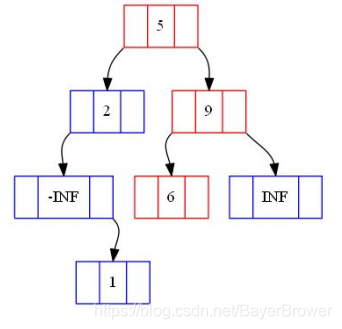
在如下BST中:
查找6:
查找3:
1 int Get(int p, int val) { 2 if (p == 0) return 0; //檢索失敗 3 if (val == a[p].val) return p; //檢索成功 4 if (val < a[p].val) return Get(a[p].l, val); //遞歸檢索左子樹 5 else return Get(a[p].r, val);//遞歸檢索右子樹 6 }
二叉查找樹的插入
在BST中插入一個新的值val(假設目前BST中不存在關鍵碼為val的節點, 若存在則不插入),與BST的檢索過程類似。
在發現要走向的p的子節點為空,說明val不存在時,直接建立關鍵碼為 val的新節點作為p的子節點。
1 void Insert(int &p, int val) { 2 if (p == 0) { 3 p = new(val); //p是引用,其父節點的l或r值會被同時更新 4 return; 5 } 6 if (val == a[p].val) return; 7 if (val < a[p].val) Insert(a[p].l, val); 8 else Insert(a[p].r, val); 9 }
二叉查找樹找後繼
在BST中, val 的後繼指的是在關鍵碼大於 val 的前提下,關鍵碼最小的節點。
初始化val為具有正無窮關鍵碼的那個節點的編號(編號為2)。然後,從根節點開始在BST中檢索val。在檢索的過程中,每經過一個節點,都檢查該節點的關鍵碼,判斷能否更新所求的後繼val。
檢索完成後,有三種可能的結果:
1.沒有找到val此時val的後繼就在已經經過的節點中,val即為所求。
2.找到了關鍵碼為val的節點p,但p沒有右子樹與上一種情況相同,val即為所求
3.找到了關鍵碼為val的節點p,且p有右子樹從p的右子節點出發,一直向左走,就找到了val的後繼
1 int GetNext(int val) { 2 int ans = 2; 3 int p = root; 4 while (p) { 5 if (val == a[p].val) { 6 if (a[p].r > 0) { 7 p = a[p].r; 8 while (a[p].l > 0) p = a[p].l; 9 ans = p; 10 } 11 break; 12 } 13 if (a[p].val > val && a[p].val < a[ans].val) ans = p; 14 p = val < a[p].val ? a[p].l : a[p].r; 15 } 16 return a[ans].val; 17 }
二叉查找樹找前驅
1 int GetPre(int val) { 2 int ans = 1; 3 int p = root; 4 while (p) { 5 if (val == a[p].val) { 6 if (a[p].l > 0) { 7 p = a[p].l; 8 while (a[p].r > 0) p = a[p].r; 9 ans = p; 10 } 11 break; 12 } 13 if (a[p].val < val && a[p].val > a[ans].val) ans = p; 14 p = val < a[p].val ? a[p].l : a[p].r; 15 } 16 return a[ans].val; 17 }
二叉查找樹的刪除
從BST中刪除關鍵碼為val的節點 首先,在BST中檢索val,得到節點p 若p的子節點個數小於2,則直接刪除p,並令p的子節點代替p的位置,與p 的父節點相連。 若p既有左子樹又有右子樹,則在BST中求出val的後繼節點next。因為next 沒有左子樹,所以可以直接刪除nest,並令next的右子樹代替nest的位置。最後, 再讓next節點代替p節點,刪除p即可。
1 void Remove(int val) { 2 //檢索val, 得到節點p 3 int &p = root; 4 while (p) { 5 if(val == a[p].val) break; 6 p = val < a[p].val ? a[p].l : a[p].r; 7 } 8 if (p == 0) return;//結點不存在 9 if (a[p].l == 0) //沒有左子樹 10 p = a[p].r; //右子樹代替p的位置,p是引用 11 else if (a[p].r == 0) //沒有右子樹 12 p = a[p].l; //左子樹代替p的位置,p是引用 13 else { //求後繼 14 int next = a[p].r; 15 while (a[next].l > 0) next = a[next].l; 16 Remove(a[next].val); //next一定沒有左子樹,直接刪除 17 a[next].l = a[p].l, a[next].r = a[p].r; //節點next代替p的位置 18 p = next; 19 } 20 }
二叉查找樹的性能分析
在隨機數據中,BST一次操作的期望複雜度是O(log n)。然而, BST很容易退化,例如在BST中依此插入一個有序序列,將會得到一條 鏈,平均每次操作的複雜度都為O(n)。 這樣的左右子樹大小相差很大的BST是不平衡的。有很多種方法可 以維持BST的平衡,從而產生了各種平衡樹。
THE END