一、前言 經過一個月來的學習,我從對面向對象一無所知到逐漸入門,圍繞著“多項式求導”,對面向對象的特性進行了探索。 我對面向對象印象最深的兩句話就是“萬物皆對象”和“高內聚、低耦合”,這三次作業也是儘量貫徹了這兩句話。 我們的作業從第一次的僅含冪函數的求導,到第二次包含正餘弦函數,再到最後函數可以嵌 ...
一、前言
經過一個月來的學習,我從對面向對象一無所知到逐漸入門,圍繞著“多項式求導”,對面向對象的特性進行了探索。
我對面向對象印象最深的兩句話就是“萬物皆對象”和“高內聚、低耦合”,這三次作業也是儘量貫徹了這兩句話。
我們的作業從第一次的僅含冪函數的求導,到第二次包含正餘弦函數,再到最後函數可以嵌套。一步步走來,面向對象的優點也逐漸浮現出來。
二、分析工具
本次作業我們用複雜度分析和UML類圖對代碼進行度量,首先介紹複雜度分析:
複雜度分析是對方法的圈複雜度進行分析,有三個衡量指標:ev(G), iv(G), v(G)
- Cyclomatic Complexity (v(G)) 圈複雜度
- Module Design Complexity (iv(G))模塊設計複雜度
模塊設計複雜度是用來衡量模塊判定結構,即模塊和其他模塊的調用關係。軟體模塊設計複雜度高意味模塊耦合度高,這將導致模塊難於隔離、維護和復用。
模塊設計複雜度是從模塊流程圖中移去那些不包含調用子模塊的判定和迴圈結構後得出的圈複雜度,因此模塊設計複雜度不能大於圈複雜度,通常是遠小於圈複雜度。
- Essential Complexity (ev(G))基本複雜度
下麵我們結合代碼對其進行說明:
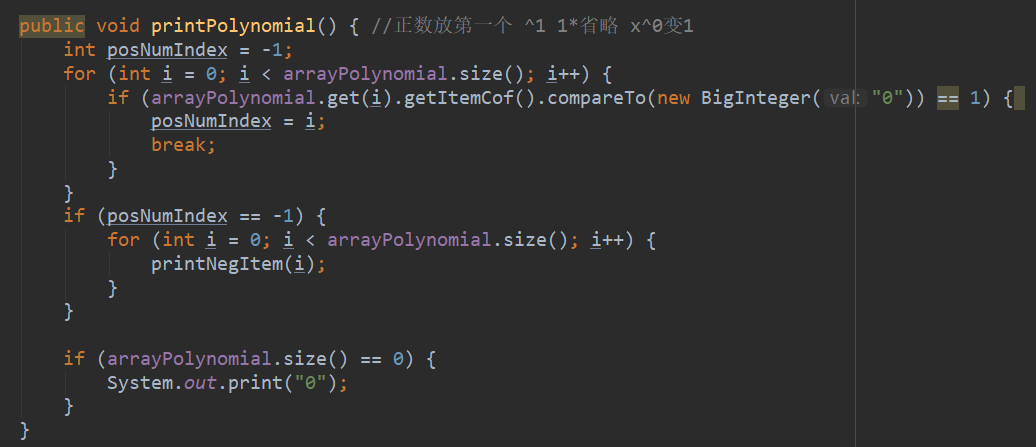
這是第一次作業列印多項式的一部分,可以看到它的複雜度是

首先我們來看v(G)的計算,畫出流程框圖,可以看出這個圖共有10個點,14條邊,則v(G) = 14+2-10 = 6
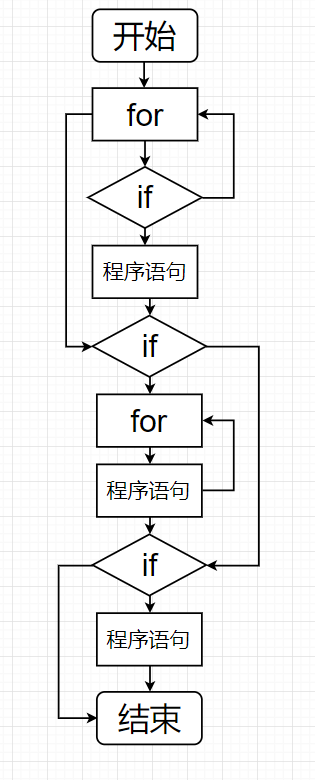
然後我們來計算iv(G),把沒有調用子方法的模塊簡化成一個點,這段代碼中只有for迴圈里if內部沒有調用子方法,因此只有這個if被簡化,簡化後的圖如下
其中有點9個,邊12條,iv(G) = 12 + 2 - 9 = 5
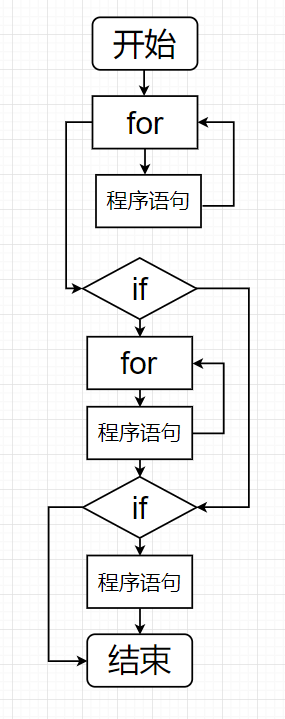
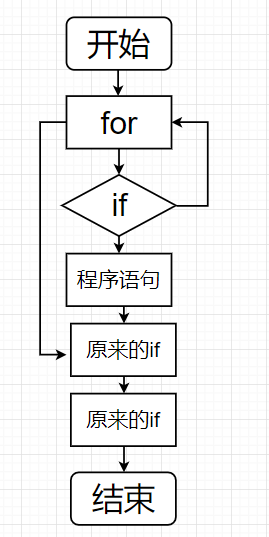
最後計算ev(G),我們要把原來流程圖結構化的部分簡化,這裡的結構化的部分指的是只有if/for只有一個入口點,我們代碼中的for迴圈就有兩個入口點,因此不能簡化(若把原代碼的break去掉就可以簡化了),具體可以查看Essential complexity - Wikipedia
所作流程圖如下,ev(G) = 8 + 2 - 7 = 3
UML類圖則是描述類與類之間關係的圖,其關係共有繼承、實現、依賴、關聯、聚合、組合六種,而這三次作業我僅用到了三種依賴,聚合與包含,其他的以後用到了再做總結。
依賴關係是一個類使用了另外一個類。
聚合關係是一個類內部有另外一個類,即has-a關係。
繼承關係是一個類繼承了另外一個類。
圖示:
依賴:
聚合:
繼承:![]()
三、代碼分析
1. 第一次作業
第一次作業的思路挺清晰的,只知道“萬物皆對象”,就把表達式分成一個個項,把表達式抽象成一個對象,把每個項抽象成一個對象,然後用正則表達式去匹配每一項,提取x的指數和繫數,然後對對每一項求導並加在表達式對象上,輸出就完事了。化簡也需要合併同類項,把正項放在第一位,繫數為1或-1不輸出,指數為1不輸出。
圈複雜度:
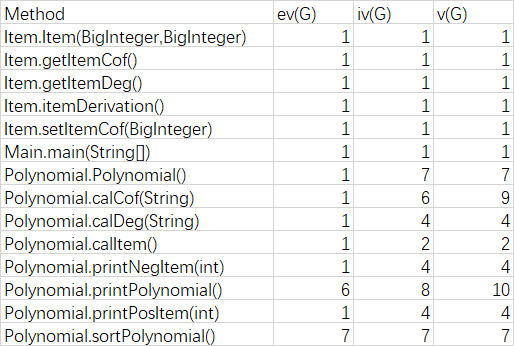
可以看出有幾個方法的圈複雜度挺高的,計算指數和繫數,列印多項式,因為這幾個方法都有很多需要判斷繫數為不為1,指數為不為1,導致有許多if-else結構。
UML類圖:第一次作業還是挺簡潔的。
第一次作業算是入門了面向對象了,我努力的運用OO的思想去做這次作業,避免了一main到底的情況,我還學到了正則表達式的使用,java語法結構等。
但是這次作業我出了好幾個BUG,1. 沒想到他們會用\f來hack,2.合併完同類項忘記刪除繫數為0的項。
這兩個BUG分別出在分析表達式和計算表達式上,都是因為沒考慮清楚才導致錯誤的。
在找BUG階段,我也使出渾身解數,第一次作業基本就是找WrongFormat大賽,畢竟這次求導太簡單了。用各種多符號,少數字的表達式去測試他們,還有合併同類項為0、爆棧的數據,比如:
1231323 + 3131321++32131++661656161
2132*x+- 13213213++2313132*x^3213132
q123213+31321*x
x+x+x+x+x+x+x+x++x++x+-x+- x
313132x^100+x^100+x^99--x^99
3*x^-1+2*x^2
+ + x + + x ++ 2131 * x ^ 2236
321321*x^x
+
-
x^
500個+x
1000個1
x+x-x-x
這次作業相對簡單,可以通過閱讀代碼來構造相應的數據來hack,有一位同學就是用“ | ”作為項與項之間的分隔,然後我構造了一個“|x”的數據他就錯了。
2.第二次作業
第二次作業和第一次作業特別相似,僅僅在因數中加入了sin(x),cos(x),其他和第一次作業是一樣的,每一項都可以用“a*x^b*sin(x)^c*cos(x)^d”來表示,因此我用了和第一次作業一樣的結構而沒有去為了相容第三次而重構代碼(主要是懶)。
圈複雜度:
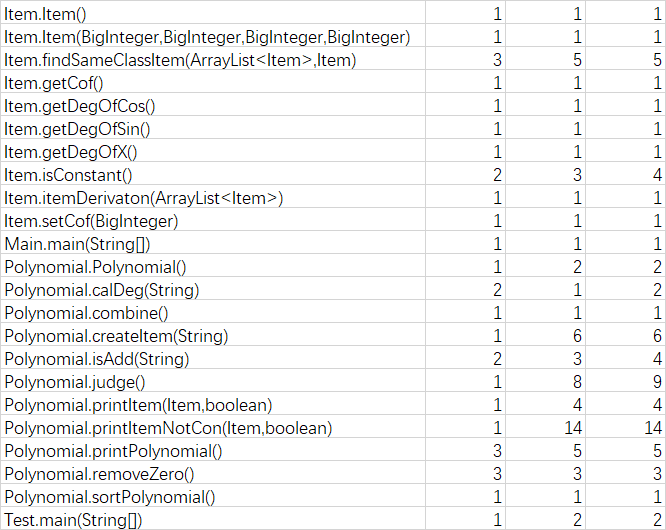
可以看到這次的圈複雜度還是在列印表達式和判斷表達式的方法比較高,依舊是那個問題需要判斷繫數為不為1,指數為不為1,導致有許多if-else結構。
UML類圖:和第一次作業差不多
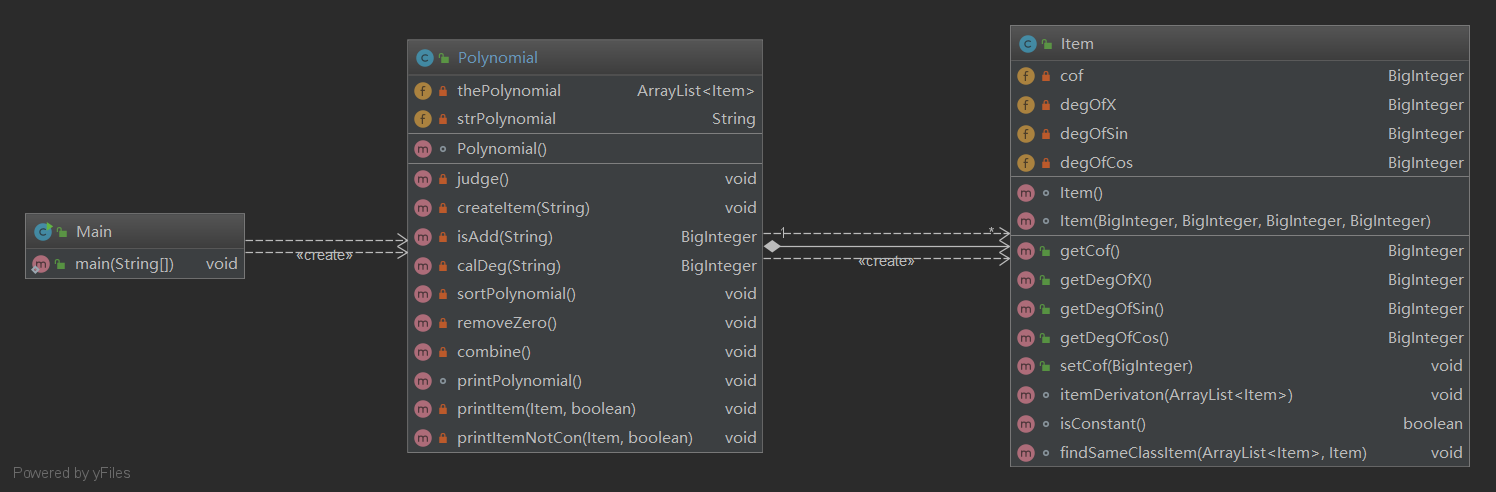
這次的化簡主要是運用cos(x)^2+sin(x)^2 = 1這個式子及變式進行化簡,用迴圈找出可以化簡的項然後合併就OK。這次作業主要是鞏固了一下麵向對象的知識點,鞏固一下正則表達式的使用,為下一次作業做準備。
這次因為和上次的題目比較像,所以寫的挺完善的也沒被找出BUG。
找BUG階段則是閱讀別人的代碼,然後構造出相應的測試點。
3. 第三次作業
第三次作業的難度陡增,它從表達式的加減乘變成了可以嵌套的模式,這就只能重構代碼了,這也揭示了一個問題:前兩次作業的代碼耦合度過高,難以修改。這次作業的思想主要是把表達式按加減號拆開,得到各個項,再把項按乘號拆開,得到因數,因數有括弧,數字,x,sin,cos五種,其中sin,cos,括弧可以嵌套表達式,然後遞歸。
圈複雜度:
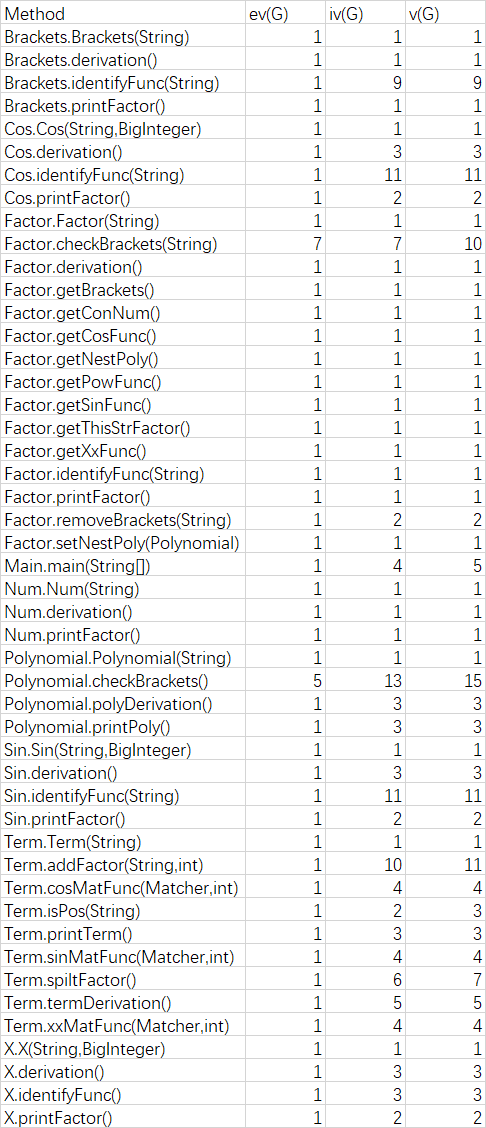
圈複雜度高的依舊是識別函數的方法,這次BUG就出在了識別上。
UML類圖:結構比前兩次作業複雜了許多
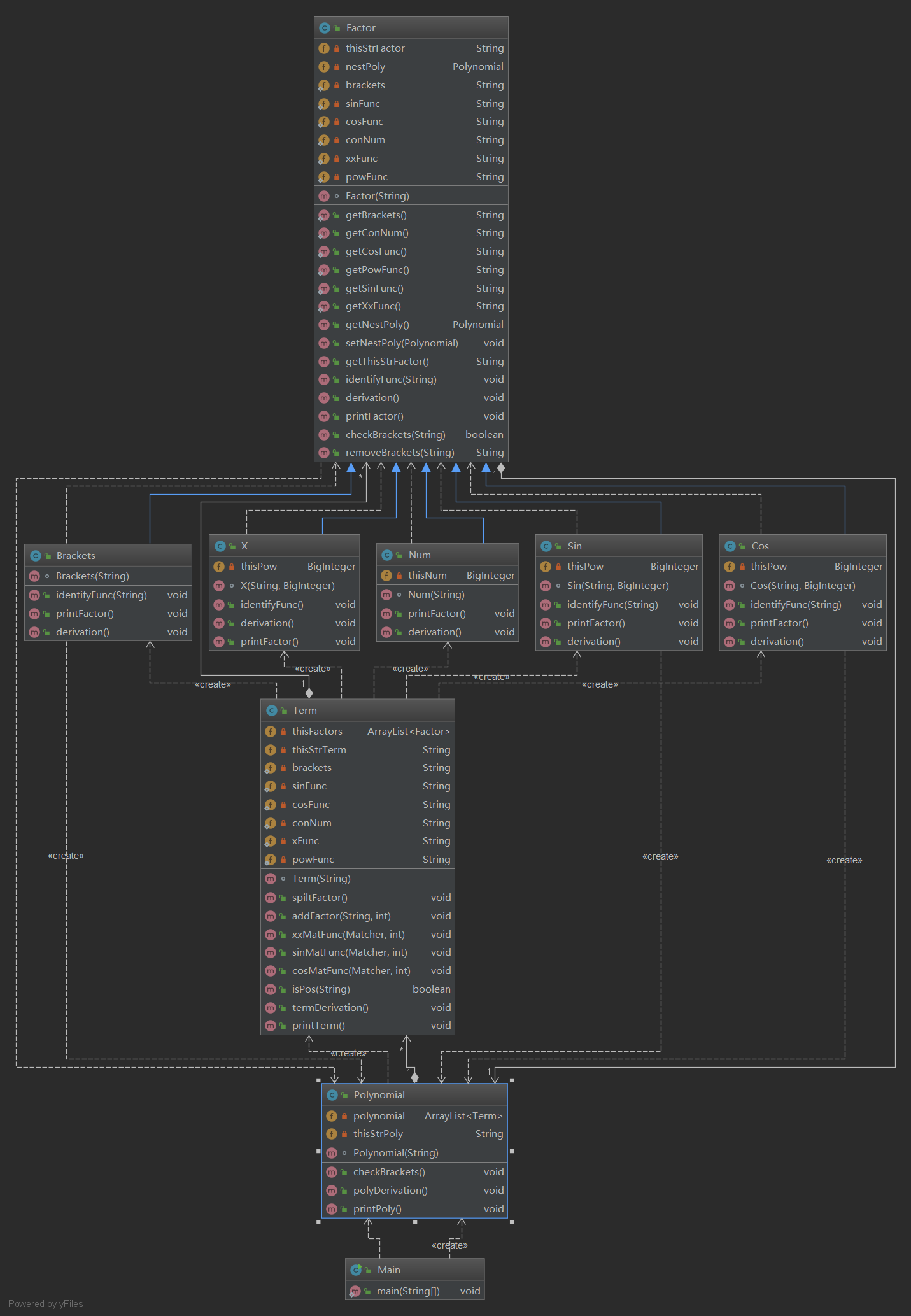
這次作業用到了繼承的思想,因數有5種,就用5個子類去繼承因數這個父類,這樣做的好處也很明顯,項是由因數構成的,可以用一個ArrayList<Factor>去存儲五種因數,而不要分開存,求導也可以直接調用重寫的求導方法Factor.derivation()。本次作業讓我對面向對象的理解又深了許多,也複習了一下遞歸的使用,遞歸真的好用。
找BUG這次也沒什麼很好的方法找,只能構建嵌套多層的因數,加各種指數去測試他們的遞歸會不會有問題,輸出會不會有問題。
這次我被找到了一個BUG,就是識別因數的時候,在很多判斷中漏了一個條件,導致有些因數識別不出來,會報WF,圈複雜度高果然容易出錯。
四、心得體會
幾次作業下來對面向對象有一定的瞭解,知道面向過程與面向對象的區別,明白了“高內聚,低耦合”的道理。在編寫代碼時,一定先用清晰的思維去構思好程式的設計框架,這樣在寫代碼的時候就不容易因為思緒混亂而寫出帶BUG的程式。寫完程式後要編寫完備的測試樣例,無論是測試自己的程式還是hack他人的程式都是極好的。
話不多說,繼續努力,面向對象,從我做起。
願諸君共勉!



