第一單元總結

来源:https://www.cnblogs.com/black-watch/archive/2019/03/26/10598993.html
-Advertisement-
Play Games

第一單元總結 作業總結 一 程式結構分析 ​ 因為在此之前並沒有接觸過 java 語言或者是與之相似的語言, 而不用說 OO 的概念, 所以一切都是全新的. 開始的時候腦子並沒有任何面向對象的概念, 類這個概念僅僅建立在 C 語言的某個 .c 文件之上, 簡單地認為 java 中的類就是 C 中的 ...


第一單元總結

作業總結

一 程式結構分析

​ 因為在此之前並沒有接觸過 java 語言或者是與之相似的語言, 而不用說 OO 的概念, 所以一切都是全新的. 開始的時候腦子並沒有任何面向對象的概念, 類這個概念僅僅建立在 C 語言的某個 .c 文件之上, 簡單地認為 java 中的類就是 C 中的 .c 文件. 所以第一次作業幾乎沒有什麼類劃分, 僅有的四個類更像是 C 中的四個函數, 而不是四個類. 第二次作業的時候毫無疑問地走向了重構道路, 雖然仍然沒有擺脫面向過程的編程方法, 但開始對類的概念有一些自己的想法, 開始嘗試著劃分類, 並用類之間的交互來實現需要的功能. 第三次作業中, 類的數量和種類大大增多, 同時類的劃分界限也明確起來, 並不是一味地當成函數集合來用. 很明顯, 這三次並不那麼令人愉快的作業經歷大大地加深了我對面向對象思想的理解. 下麵是三次作業的詳細分析:

三次作業類圖

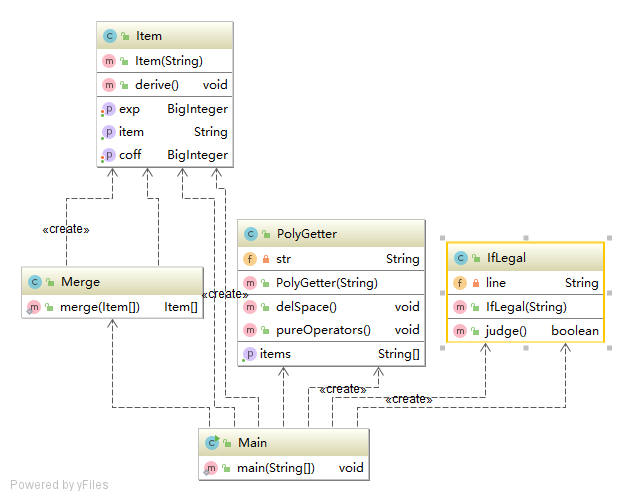
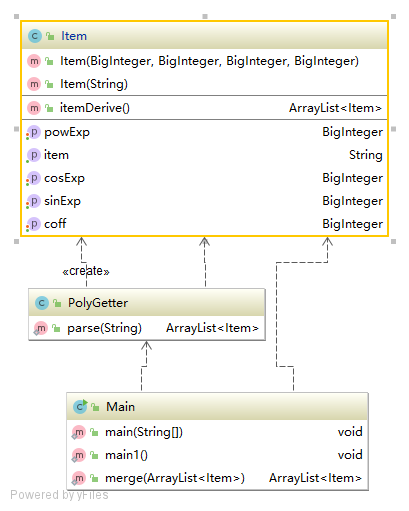
三次作業度量

  • 名詞說明:

    • OCavg:

      Calculates the average cyclomatic complexity of the non-abstract methods in each class. Inherited methods are not counted for purposes of this metric.

      類平均圈複雜度, 繼承類不計入

    • WMC:

      Calculates the total cyclomatic complexity of the methods in each class.

      類總圈複雜度

    • ev(G):

      Calculates the essential complexity of each non-abstract method. Essential complexity is a graph-theoretic measure of just how ill-structured a method's control flow is. Essential complexity ranges from 1 to v(G), the cyclomatic complexity of the method.

      非抽象方法的基本複雜度, 基本複雜度是一個圖論度量理論, 用來度量一個方法的控制流結構有多差, 基本複雜度的範圍是 1 到 v(G)

    • iv(G):

      Calculates the design complexity of a method. The design complexity is related to how interlinked a methods control flow is with calls to other methods. Design complexity ranges from 1 to v(G), the cyclomatic complexity of the method. Design complexity also represents the minimal number of tests necessary to exercise the integration of the method with the methods it calls.

      設計複雜度, 度量方法控制流與其他方法之間的耦合程度, 設計複雜度的範圍是 1 到 v(G)

    • v(G):

      Calculates the cyclomatic complexity of each non-abstract method. Cyclomatic complexity is a measure of the number of distinct execution paths through each method. This can also be considered as the minimal number of tests necessary to completely exercise a method's control flow. In practice, this is 1 + the number of if's, while's, for's, do's, switch cases, catches, conditional expressions, &&'s and ||'s in the method.

      圈複雜度, 度量每個中不同路徑執行的數量

  • 度量結果:

    • 第一次:

      Class metrics:

      class OCavg WMC
      com.lm.Merge 6.0 6.0
      com.lm.Main 6.0 6.0
      com.lm.Item 2.857142857142857 20.0
      com.lm.IfLegal 4.0 8.0
      Total 54.0

      Method metrics:

      method ev(G) iv(G) v(G)
      com.lm.PolyGetter.pureOperators() 1.0 11.0 11.0
      com.lm.PolyGetter.PolyGetter(String) 1.0 1.0 1.0
      com.lm.PolyGetter.getItems() 1.0 3.0 3.0
      com.lm.PolyGetter.delSpace() 3.0 3.0 4.0
      com.lm.Merge.merge(Item[]) 5.0 5.0 6.0
      com.lm.Main.main(String[]) 2.0 6.0 6.0
      com.lm.Item.setExp(BigInteger) 1.0 1.0 1.0
      com.lm.Item.setCoff(BigInteger) 1.0 1.0 1.0
      com.lm.Item.Item(String) 1.0 6.0 7.0
      com.lm.Item.getItem() 3.0 6.0 7.0
      com.lm.Item.getExp() 1.0 1.0 1.0
      com.lm.Item.getCoff() 1.0 1.0 1.0
      com.lm.Item.derive() 1.0 3.0 3.0
      com.lm.IfLegal.judge() 6.0 4.0 8.0
      com.lm.IfLegal.IfLegal(String) 1.0 1.0 1.0
      Total 29.0 53.0 61.0
      Average 1.9333333333333333 3.533333333333333 4.066666666666666

    • 第二次:

      Class metrics:

      class OCavg WMC
      com.mypkg.PolyGetter 6.0 6.0
      com.mypkg.Main 5.0 15.0
      com.mypkg.Item 2.4166666666666665 29.0
      Total 50.0
      Average 3.125 16.666666666666668

      Method metrics:

      method ev(G) iv(G) v(G)
      com.mypkg.PolyGetter.parse(String) 6.0 4.0 7.0
      com.mypkg.Main.merge(ArrayList) 4.0 7.0 7.0
      com.mypkg.Main.main1() 2.0 8.0 8.0
      com.mypkg.Main.main(String[]) 1.0 2.0 2.0
      com.mypkg.Item.setSinExp(BigInteger) 1.0 1.0 1.0
      com.mypkg.Item.setPowExp(BigInteger) 1.0 1.0 1.0
      com.mypkg.Item.setCosExp(BigInteger) 1.0 1.0 1.0
      com.mypkg.Item.setCoff(BigInteger) 1.0 1.0 1.0
      com.mypkg.Item.itemDerive() 1.0 1.0 1.0
      com.mypkg.Item.Item(String) 3.0 11.0 12.0
      com.mypkg.Item.Item(BigInteger,BigInteger,BigInteger,BigInteger) 1.0 1.0 1.0
      com.mypkg.Item.getSinExp() 1.0 1.0 1.0
      com.mypkg.Item.getPowExp() 1.0 1.0 1.0
      com.mypkg.Item.getItem() 1.0 9.0 9.0
      com.mypkg.Item.getCosExp() 1.0 1.0 1.0
      com.mypkg.Item.getCoff() 1.0 1.0 1.0
      Total 27.0 51.0 55.0
      Average 1.6875 3.1875 3.4375

    • 第三次:

      Class metrics:

      class OCavg WMC
      com.mypkg.Sin 6.333333333333333 19.0
      com.mypkg.Production 3.875 31.0
      com.mypkg.Pow 3.3333333333333335 10.0
      com.mypkg.Main 4.2 21.0
      com.mypkg.Int 1.0 3.0
      com.mypkg.Cos 6.333333333333333 19.0
      com.mypkg.Conbination 22.0 66.0
      Total 169.0
      Average 6.035714285714286 24.142857142857142

      Method metrics:

      method ev(G) iv(G) v(G)
      com.mypkg.Sin.Sin(String) 1.0 12.0 12.0
      com.mypkg.Sin.print() 1.0 6.0 6.0
      com.mypkg.Sin.derive() 1.0 8.0 8.0
      com.mypkg.Production.Production() 1.0 1.0 1.0
      com.mypkg.Production.print() 1.0 14.0 14.0
      com.mypkg.Production.derive() 1.0 11.0 11.0
      com.mypkg.Production.add(Sin) 1.0 1.0 1.0
      com.mypkg.Production.add(Pow) 1.0 1.0 1.0
      com.mypkg.Production.add(Int) 1.0 1.0 1.0
      com.mypkg.Production.add(Cos) 1.0 1.0 1.0
      com.mypkg.Production.add(Conbination) 1.0 1.0 1.0
      com.mypkg.Pow.print() 1.0 3.0 3.0
      com.mypkg.Pow.Pow(String) 1.0 3.0 3.0
      com.mypkg.Pow.derive() 1.0 4.0 4.0
      com.mypkg.Main.pureString(String) 1.0 11.0 12.0
      com.mypkg.Main.nextIndex(String,int) 4.0 4.0 6.0
      com.mypkg.Main.main1(String[]) 4.0 4.0 4.0
      com.mypkg.Main.main(String[]) 1.0 2.0 2.0
      com.mypkg.Main.bracketMatch(String) 3.0 3.0 5.0
      com.mypkg.Int.print() 1.0 1.0 1.0
      com.mypkg.Int.Int(String) 1.0 1.0 1.0
      com.mypkg.Int.derive() 1.0 1.0 1.0
      com.mypkg.Cos.print() 1.0 6.0 6.0
      com.mypkg.Cos.derive() 1.0 8.0 8.0
      com.mypkg.Cos.Cos(String) 1.0 12.0 12.0
      com.mypkg.Conbination.print() 1.0 9.0 10.0
      com.mypkg.Conbination.derive() 1.0 9.0 10.0
      com.mypkg.Conbination.Conbination(String) 22.0 51.0 66.0
      Total 57.0 189.0 211.0
      Average 2.0357142857142856 6.75 7.535714285714286

優缺點分析:

  1. 從上面的類圖和度量表看到, 我在這幾次作業中並沒有使用繼承和介面, 一方面是因為我覺得自己對於繼承和介面的概念不夠熟悉, 怕亂用寫出 BUG, 加大自己的工作量, 另一方面, 我對於介面的作用確實不理解, 也不會用(直到現在仍然是認為介面只是形式上規定了繼承於他的類應該有哪些方法, 而和我不用介面分別在各個類中去實現這些方法並沒有什麼實質區別, 僅僅是形式上而已).
  2. 從三次作業的度量值分析可以看到, 我幾次的代碼都比較病態, 尤其是到了第三次, 幾乎所有的代碼都集中到了 Conbination 類, 而且在 Conbination 類中的構造方法也是占據了極高的比例, 方法, 類之間的耦合度極高, 這些都暴露出來我編程思想不夠嚴謹的問題, 我希望在以後的學習中努力改變自己這種病態的代碼結構.
  3. 從三次類圖的遞進發展來看, 類漸趨於完善, 可以看到進步也是存在的. 這三次作業最大的收穫就是對面向對象思想的理解得到了極大程度地加深, 尤其是看到第三次作業提示構造表達式樹, 有一種豁然開朗地感覺. 其次, 則是正則表達式, 在 OO 課開課之前多次聽說正則表達式地大名, 但都是好像很叼地樣子, 覺得應該不是一個初學者地我能掌握地東西, 所以沒怎麼看. 但是經過三次作業地磨礪, 我覺得自己對正則表達式已經有了一定的瞭解, 開始覺得正則表達式很難, 接觸之後又覺得正則表達式就那麼回事, 挺簡單的, 然後大正則爆棧, 開始瞭解一些和正則相關的深入一些地知識, 如: DFA, NFA, 回溯等概念. 又開始覺得正則是個博大精深的東西. 相信在經歷了 OO 之後, 我一定能很好地運用正則.

二 程式BUG分析

第一次作業

​ 第一次作業一共兩個已知 BUG , 分別是:

​ 超大整數陷阱: 我在比較兩個超大整數的時候, 想當然地調用了 intValue() 方法, 將他們轉換 int 型數據比較, 未考慮超大整數溢出, 結果出錯了. 應該調用 Compare() 方法進行超大整數之間的比較.

​ 大正則陷阱: 試圖用一個超長的正則表達式匹配整個表達式, 結果爆棧. 正確方法應該是分項匹配. 下麵貼出大正則反例片段:

Pattern q = Pattern.compile("^" +
                "\\s*[+-]?\\s*(([+-]?\\d+)" +
                "|(([+-]|[+-]?\\d+\\s*\\*)?\\s*x\\s*(\\^\\s*[+-]?\\d+)?))" +
                "(\\s*[+-]\\s*((([+-]|[+-]?\\d+\\s*\\*)?\\s*" +
                "x(\\s*\\^\\s*[+-]?\\d+)?)|[+-]?\\d+))*" +
                "+" +
                "\\s*$");
        Matcher n = q.matcher(line);
        if (n.find()) {
            return true;
        }
        Pattern p = Pattern.compile("^" +
                "\\s*[+-]?\\s*(([+-]?\\d+)" +
                "|(([+-]|[+-]?\\d+\\s*\\*)?\\s*x\\s*(\\^\\s*[+-]?\\d+)?))" +
                "(\\s*[+-]\\s*((([+-]|[+-]?\\d+\\s*\\*)?\\s*" +
                "x(\\s*\\^\\s*[+-]?\\d+)?)|[+-]?\\d+))*" +
                "\\s*$");
        Matcher m = p.matcher(line);
        return m.find();

第二次作業

​ 第二次作業未發現 BUG

第三次作業

​ 第三次作業發現一個潛在 BUG ( 未被測出來, 但確實存在 ), 就是老僧長談地深層遞歸爆棧, 目前並沒有想到什麼好的解決辦法. 另一個已知 BUG 是 sin(- 1) 會判對, 原因是我在處理原始字元串地時候採用了窮舉帶符號數被空格截斷地情況, 但是窮舉不夠充分, 僅考慮到了冪指數, 以及最外層的整數繫數和常數項, 未考慮到整數作為因數出現嵌套的情況, 故錯.

三 Hack體驗

​ 第一次作業因為超大整數溢出直接沒進互測, 沒有任何體驗....

​ 第二次作業沒有被炸, 體驗良好....

​ 第三次被炸了幾個點....

​ 總結幾次互測的體驗, 發現 BUG 高發區集中在輸入格式處理上面, 大正則爆棧, 情況考慮不夠完善等. 另外很多同學的 BUG 是由於優化導致的, 以至於將優化方法或者類註釋掉就通過了....另外有一點要說的是, 希望提交間隔可以適當縮短一點, 畢竟有的數據點自己驗證起來也不好驗證, 特別是經過一系列恆等變換之後.

四 建模重構

​ 關於重構, 初步的想法是構建一個運算介面, 運算介面包括求導, toString(), 簡單化簡(僅僅是同類項合併, 指數合併等)方法. 然後構建 Sin Cos Pow Com Mul 類繼承運算介面, 構建表達式樹, 實現鏈式求導, 指導書上說構建嵌套類, 但我不知道怎麼構造, 只能通過在 Sin Cos Pow 內部使用嵌套標記來表示該對象是否嵌套了下一級, 希望在之後公佈的優秀代碼種學會如何構建嵌套類. 至於化簡, 隨緣吧...


您的分享是我們最大的動力!

-Advertisement-
Play Games
更多相關文章
  • 面向對象第一單元博客作業
    通過第一單元的學習，首先是對面向對象程式設計思想有了一個大致的認識。其次對於面向對象語言的各種概念和機制有了大致的瞭解併進行了應用（如類、方法、繼承、介面、try-catch機制等）。通過自己課下練習、與同學討論和在課上通過老師對作業的總結講解，能夠明確感受到這樣一種思想與之前接觸的面向過程的一些程... ...
  • OO第一單元(求導)單元總結
    OO第一單元(求導)單元總結 這是我們oo課程的第一個單元，也是意在讓我們接觸瞭解掌握oo思想的一個單元，這個單元的作業以求導為主題，從一開始的加減多項式求導再到最後的嵌套多項式求導，難度逐漸提高，編程思想也逐步深入面向對象，如果說前兩次作業還可以用C語言的面向過程的思想去對付，那麼第三次作業可以說 ...
  • 聊聊在AOP模式下的緩存方案
    面向方法的數據集緩存 使用了autofac做為ioc容器，使用Autofac.Extras.DynamicProxy2作為方法攔截器，緩存面向方法，直接在方法上添加CachingAttribute特性即可。 緩存註冊流程 1. 關於方法攔截器 1. 緩存名稱設計 1. 添加ioc 1. 添加攔截器與 ...
  • BUAA OO 2019 第一單元作業總結
    [TOC] 總 本博文是2019年北航面向對象（OO）課程第一單元作業（多項式求導）的總結。三次作業的要求大致如下： 第一次作業：簡單冪函數的求導，如 $1 + x^5 + 4 x^3$ 第二次作業：簡單冪函數和簡單正餘弦函數的求導，如 $ 5 sin(x)^2+5 cos(x) cos(x)+12 ...
  • 關於Java中構造方法的問題以及回答
    構造方法 概念： 又叫 構造器，區分於傳統的方法，是一個在創建對象時被系統自動調用的特殊方法 作用： 一：為對象進行初始化（成員變數）的工作 二：為對象在堆記憶體中開闢獨立的記憶體空間 定義格式： 訪問修飾符 方法名(){ } 用法： 只能通過new關鍵字進行調用 註意事項： 一：方法名必須和類名保持一 ...
  • 2019北航OO第一單元作業總結
    一、前三次作業內容分析總結 前言 前三次作業，我提交了三次，但是有效作業只有兩次，最後一次作業沒能實現多項式求導的基本功能因此無疾而終，反思留給後文再續，首先我介紹一下這三次作業，三次作業圍繞著多項式求導展開，輸出目的都是一致的，即對輸入的多項式進行求導，將求導結果列印到顯示屏，作業難度遞增，每一次 ...
  • 掃描二維碼登錄實現原理分析
    記得比較早使用手機掃碼登錄是網頁版微信，這種免去輸入繁瑣的賬號密碼，拿起手機掃一掃就可以登錄的方式一開始還是比較驚艷的，確實使用起來很方便。 那它是如何實現的呢？我們來簡單研究下。（以淘寶網二維碼登錄為例） 首先，任何一個二維碼表示的都是一串字元串。 我們打開淘寶登錄頁面： "https://log ...
  • OO第一單元總結
    第一次作業 第一次作業需要完成的任務為簡單多項式導函數的求解。 思路 因為僅僅是簡單多項式的求導，所以求導本身沒有什麼可說的，直接套用冪函數的求導公式就行了，主要的精力是花在了正則表達式上。這裡推薦兩個網站： https://github.com/ziishaned/learn regex http ...
一周排行
    -Advertisement-
    Play Games
  • 移動開發（一）：使用.NET MAUI開發第一個安卓APP
    移動開發（一）：使用.NET MAUI開發第一個安卓APP 對於工作多年的C#程式員來說，近來想嘗試開發一款安卓APP，考慮了很久最終選擇使用.NET MAUI這個微軟官方的框架來嘗試體驗開發安卓APP，畢竟是使用Visual Studio開發工具，使用起來也比較的順手，結合微軟官方的教程進行了安卓 ...
  • wpf ToggleButton選中效果和一個登錄界面
    前言 QuestPDF 是一個開源 .NET 庫，用於生成 PDF 文檔。使用了C# Fluent API方式可簡化開發、減少錯誤並提高工作效率。利用它可以輕鬆生成 PDF 報告、發票、導出文件等。 項目介紹 QuestPDF 是一個革命性的開源 .NET 庫，它徹底改變了我們生成 PDF 文檔的方 ...
  • 彈幕樹洞項目功能新增篇
    項目地址 項目後端地址： https://github.com/ZyPLJ/ZYTteeHole 項目前端頁面地址： ZyPLJ/TreeHoleVue (github.com) https://github.com/ZyPLJ/TreeHoleVue 目前項目測試訪問地址： http://tree ...
  • 第27篇 sqlserver2022詳細安裝步驟
    話不多說，直接開乾 一.下載 1.官方鏈接下載： https://www.microsoft.com/zh-cn/sql-server/sql-server-downloads 2.在下載目錄中找到下麵這個小的安裝包 SQL2022-SSEI-Dev.exe，運行開始下載SQL server； 二. ...
  • .NET 開源高性能 MQTT 類庫
    前言 隨著物聯網（IoT）技術的迅猛發展，MQTT（消息隊列遙測傳輸）協議憑藉其輕量級和高效性，已成為眾多物聯網應用的首選通信標準。 MQTTnet 作為一個高性能的 .NET 開源庫，為 .NET 平臺上的 MQTT 客戶端與伺服器開發提供了強大的支持。 本文將全面介紹 MQTTnet 的核心功能 ...
  • Serilog文檔翻譯系列（六） - 可用的接收器、增強器、格式化輸出
    Serilog支持多種接收器用於日誌存儲，增強器用於添加屬性，LogContext管理動態屬性，支持多種輸出格式包括純文本、JSON及ExpressionTemplate。還提供了自定義格式化選項，適用於不同需求。 ...
  • 警惕 Visual Studio 屬性求值副作用導致邏輯不符合預期
    目錄簡介獲取 HTML 文檔解析 HTML 文檔測試參考文章 簡介 動態內容網站使用 JavaScript 腳本動態檢索和渲染數據，爬取信息時需要模擬瀏覽器行為，否則獲取到的源碼基本是空的。 本文使用的爬取步驟如下： 使用 Selenium 獲取渲染後的 HTML 文檔 使用 HtmlAgility ...
  • [使用目前最新版]HybridCLR6.9.0+YooAsset2.2.4實現純C# Unity熱更新方案 (一)
    1.前言 什麼是熱更新 游戲或者軟體更新時，無需重新下載客戶端進行安裝，而是在應用程式啟動的情況下，在內部進行資源或者代碼更新 Unity目前常用熱更新解決方案 HybridCLR，Xlua，ILRuntime等 Unity目前常用資源管理解決方案 AssetBundles，Addressable， ...
  • 在 ASP.NET Core Web API 中使用操作篩選器統一處理通用操作
    本文章主要是在C# ASP.NET Core Web API框架實現向手機發送驗證碼簡訊功能。這裡我選擇是一個互億無線簡訊驗證碼平臺，其實像阿裡雲，騰訊雲上面也可以。 首先我們先去 互億無線 https://www.ihuyi.com/api/sms.html 去註冊一個賬號 註冊完成賬號後，它會送 ...
  • 第28篇 如何.net中實現高效可靠數據同步api
    通過以下方式可以高效，並保證數據同步的可靠性 1.API設計 使用RESTful設計，確保API端點明確，並使用適當的HTTP方法（如POST用於創建，PUT用於更新）。 設計清晰的請求和響應模型，以確保客戶端能夠理解預期格式。 2.數據驗證 在伺服器端進行嚴格的數據驗證，確保接收到的數據符合預期格 ...
所有分類