[TOC] 總 本博文是2019年北航面向對象(OO)課程第一單元作業(多項式求導)的總結。三次作業的要求大致如下: 第一次作業:簡單冪函數的求導,如 $1 + x^5 + 4 x^3$ 第二次作業:簡單冪函數和簡單正餘弦函數的求導,如 $ 5 sin(x)^2+5 cos(x) cos(x)+12 ...
目錄
總
本博文是2019年北航面向對象(OO)課程第一單元作業(多項式求導)的總結。三次作業的要求大致如下:
- 第一次作業:簡單冪函數的求導,如 \(1 + x^5 + 4 * x^3\)
- 第二次作業:簡單冪函數和簡單正餘弦函數的求導,如 \(-5*sin(x)^2+5*cos(x)*cos(x)+12*x^2\)
- 第三次作業:簡單冪函數和有嵌套的正餘弦函數的求導,如 \(2*(cos(x) + 1)*cos((2*x)) - sin(x)*sin((2*x))\)
源代碼及項目要求均已發佈到 github ,讀者可以下載檢查。以下將對這一單元作業進行簡單總結。
架構
項目的總體構架參考 \(MVC\) 模式,將運算與輸入輸出分離。由於輸入輸出都是在 \(console\) 完成的,因此並沒有 \(view\) 類,但 \(Model\) 和 \(Controller\) 都有其對應類。
Controller
輸入處理類 \(PolyBuild\) ,負責將輸入字元串組織成一個 \(Poly\) 對象。其中按層次包含五個解析方法:
- \(parsePoly\)
- \(parseItem\)
- \(parseFactor\)
- \(parseElement\)
- \(parseTri\)
方法的功能顯而易見,採取遞歸下降法應用有限狀態機對字元串進行解析。
Model
\(Model\) 對應 \(Package\ Poly\) 。如下 \(UML\) 圖所示,我將多項式分為四個層次:
- \(Element\) :底層類,構成多項式的最基本元素,也是因數的底數。包括 \(Const\), \(Var\), 和 \(Tri\) 。
- \(Factor\) :因數類,構成項的單元,屬於指數函數。由一個 \(Element\) 和其對應的 \(exp\) 對應。
- \(Item\) :項類,構成多項式的單元,由多個 \(Factor\) 或表達式因數相乘組成。
- \(Poly\) :頂層類,由多個 \(Item\) 相加構成。
每個類實現各自的求導方法和輸出方法( \(toString()\) ) 。
輸入處理
處理輸入字元串時,我採用了遞歸下降法,按層用狀態機進行處理。狀態機如圖:
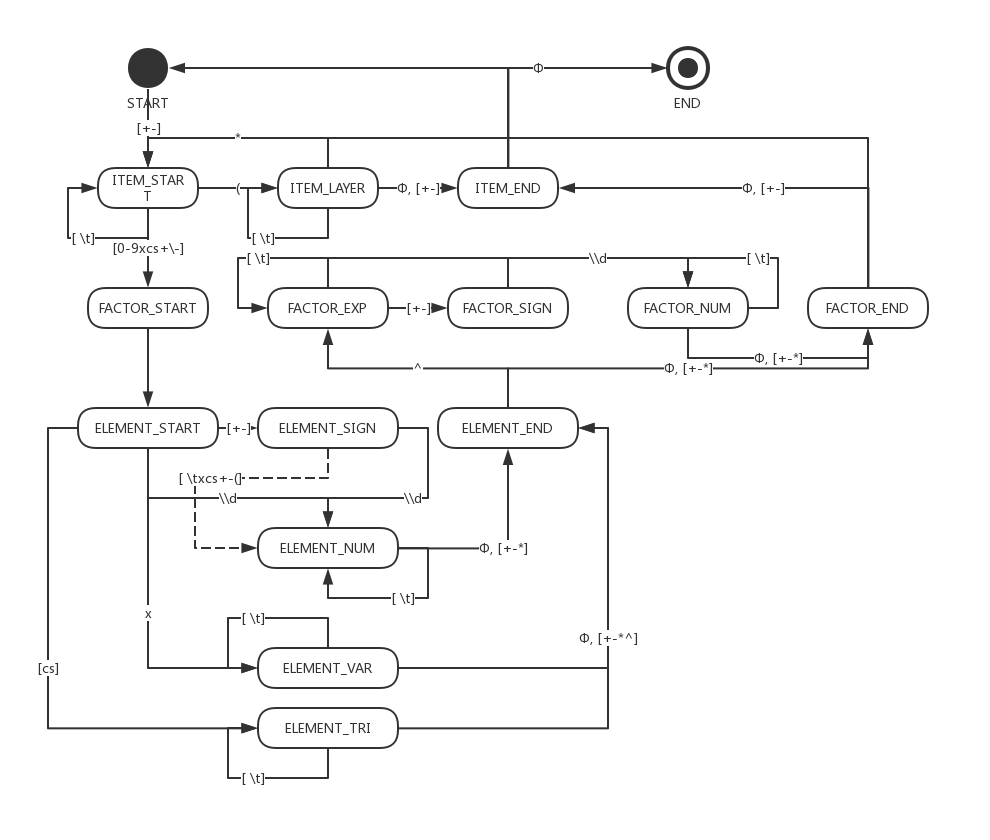
上圖為示意圖,圖中狀態可能附加處理操作,並沒有列出,讀者可以下載代碼查看。虛線表示狀態轉移時,輸入字元串會被改變。線上字元表示狀態轉移規則,即當前游標下的字元,但並不是每次狀態轉移游標都會移至下一位。\(\phi\) 表示游標到達字元串結尾。
代碼靜態分析
以下使用 \(Metrics\) 和 \(Statistics\) 插件對最終項目代碼進行靜態分析。
行數
| Source File | Total Lines | Source Code Lines | Source Code Lines[%] | Comment Lines | Comment Lines[%] | Blank Lines | Blank Lines[%] |
|---|---|---|---|---|---|---|---|
| Const.java | 88 | 68 | 0.77 | 4 | 0.04 | 16 | 0.18 |
| Derivable.java | 20 | 14 | 0.70 | 0 | 0.0 | 6 | 0.30 |
| Element.java | 60 | 44 | 0.73 | 4 | 0.06 | 12 | 0.20 |
| Factor.java | 146 | 113 | 0.77 | 11 | 0.07 | 22 | 0.15 |
| Item.java | 294 | 255 | 0.86 | 8 | 0.02 | 31 | 0.10 |
| Poly.java | 189 | 158 | 0.83 | 8 | 0.04 | 23 | 0.12 |
| PolyBuild.java | 348 | 307 | 0.88 | 11 | 0.03 | 30 | 0.08 |
| PolyBuildTest.java | 30 | 24 | 0.80 | 0 | 0.0 | 6 | 0.20 |
| Se.java | 7 | 7 | 1.00 | 0 | 0.0 | 0 | 0.0 |
| Tri.java | 71 | 56 | 0.78 | 7 | 0.09 | 8 | 0.11 |
| TriParseException.java | 2 | 2 | 1.00 | 0 | 0.0 | 0 | 0.00 |
| TypeEnum.java | 7 | 6 | 0.85 | 0 | 0.0 | 1 | 0.14 |
| Var.java | 25 | 19 | 0.76 | 0 | 0.0 | 6 | 0.24 |
可見代碼中註釋比例偏低,但空行比例較高。類長度和其複雜度成正比。其中 \(PolyBuild\) 由於包含輸入狀態機,複雜度最高;\(Poly\) , \(Item\), \(Factor\) 三類的求導操作較複雜,複雜度次之。
方法複雜度
| class | OCavg | WMC |
|---|---|---|
| poly.element.Const | 1.23 | 16.0 |
| poly.element.Element | 1.00 | 7.0 |
| poly.element.Tri | 2.00 | 12.0 |
| poly.element.TypeEnum | 0.0 | |
| poly.element.Var | 1.00 | 4.0 |
| poly.Factor | 1.55 | 28.0 |
| poly.Item | 2.28 | 64.0 |
| poly.Poly | 2.04 | 43.0 |
| PolyBuild | 8.37 | 67.0 |
| PolyBuild.StringIterator | 1.42 | 20.0 |
| PolyBuildTest | 1.00 | 4.0 |
| Se | 0.0 | |
| TriParseException | 0.0 | |
| Total | 265.0 | |
| Average | 2.154471544715447 | 20.384615384615383 |
可見 \(PolyBuild\) 類的複雜度最高,約為平均值的 \(4\) 倍。而加入權重計算時,\(PolyBuild\) 和 \(Item\) 類複雜度基本相同。
UML 類圖
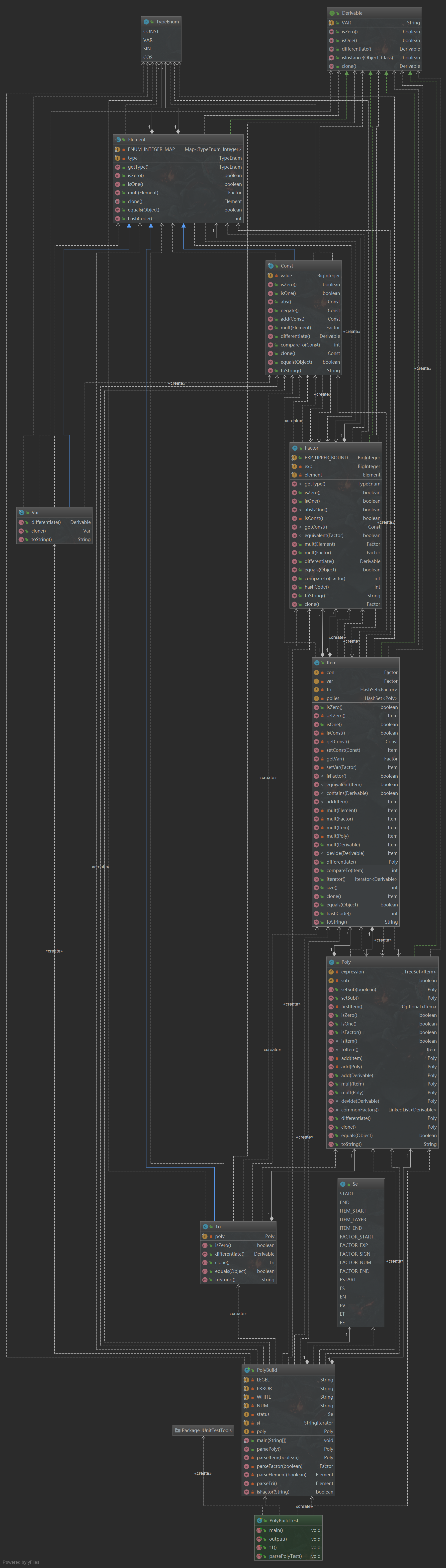
優點
類的內劇度高,類間邏輯關係清晰。\(UML\) 圖中從上至下為 \(Element\), \(Factor\), \(Item\), \(Poly\) 類,與邏輯關係相同。說明每個類都直接與其前驅類相關,而與其他類關聯度較低。
缺點
\(Item\), \(Poly\) 類的複雜度較高,尤其在求導時會進入遞歸,給調試造成困擾。
坑
此處記錄了一些在開發過程中遇到的 \(Bug\) ,希望通過反思總結警醒自己。按照這些 \(Bug\) 的出現位置,我將其大致分為輸入、運算以及輸出三個部分。每個部分都多多少少有一些 \(Bug\) ,證實了老師所說“不存在沒有 \(Bug\) 的代碼”。許多 \(Bug\) 十分隱蔽,需要大量測試才能發現。因此即使從邏輯上完備的測試了代碼,仍然需要更多測試,以檢測正確性。
輸入
輸入處理在這單元作業中最為繁瑣且易出錯,其原因主要在於識別非法輸入。正確識別合法的字元串並不困難,但一不小心很有可能將非法字元串當作合法輸入進行處理。結合被檢查出的 \(Bug\) ,我發現我對於字元出現的不同組合仍然考慮不全,因此將一些非法字元串誤認為合法進行解析。發現這個問題後,我在狀態機的轉移圖中檢查了所有可能出現的字元,這才避免了後續輸入上的 \(Bug\) 。輸入部分的 \(Bug\) 全部出現在解析類 \(PolyBuild\) 中。
非法的空白字元
在第一次作業中,最關鍵的 \(Bug\) 出現在非法的空白字元。由於允許的空白字元只有
位置
\(PolyBuild.main(String[])\)
樣例輸入
\f 1 + x在調用 \(trim\) 方法時 \(\f\) 將被刪去。但 \(\f\) 的存在使整體字元串不合法。因此這樣的處理會將一些包含非法空白字元的輸入當作合法輸入處理。
解決方法
針對非法空白字元的解決方法主要有兩個:
- 在獲得輸入後進行合法字元篩查。若輸入中存在非法字元則直接報錯,不進行後續處理。這種方法簡單直觀,且向後相容性更強。當需求有變化時只需要在合法字元集中加入對應的字元即可。
- 在處理字元串時檢查,例如在狀態機中檢查每個位置的字元是否合法。這種方法的耦合度較高,因為合法字元集分散在狀態機各處,且判斷邏輯複雜,不易發現 \(Bug\) 。但優點在於,這樣的方法可以提高效率。輸入合法性不需要單獨判斷,而是在處理輸入的同時進行。
反思
這一問題的原因在於沒有區分空白字元的合法性,誤認為空白字元即合法。
輸入的簡並處理
在第一次作業指導書中就提到
表達式由加法和減法運算符連接若幹項組成…在第一項之前,可以帶一個正號或者負號
這樣的要求就使得第一項前的運算符變成可選項,但後續各項都可以解析為一個運算符(\([+-]\))和一個項的形式。為了統一每項的解析方式,我在處理字元串前將其 \(trim\) 併在其頭部加入 \(“+0”\) 。這樣的處理可以簡並以下情況
12 * x -> +012 * x
+12 * x -> +0+12 * x
+ 12 * x -> +0+ 12 * x
+ +12 * x -> +0+ +12 * x同時考慮到如下的以 \(x\) 開頭的表達式
x ^ 2我對字元串的首個非空白字元進行了特判。若其為 \(x\) 則只補全 \(“+”\) 而不輸出 \(“0”\) 。即
x ^ 2 -> +x ^ 2位置
\(PolyBuild.main(String[])\)
樣例輸入
*x -> +0*x由輸入可以看出,原本非法的表達式被當作合法輸入進行解析。這一問題的出現即是因為事先沒有考慮到 \(“*”\) 作為表達式第一個字元出現的可能性。但從邏輯的角度看,\([+-*\^0-9x]\) 均為合法字元,應考慮到其在字元串開頭出現的可能性。
解決方法
最直接且行之有效的解決方法是加入對於 \(“*”\) 的特判。若 \(“*”\) 是字元串的首個非空字元,則報錯。但這樣的判斷顯然不夠簡潔。
另一種方法是判斷字元串的首個非空字元是否為操作符 \([+-]\) ,若非,則在字元串(\(trim\) 前)的開頭加入 \(“+”\) 。可以證明,這種方法可以完美的保留原輸入的合法性。
反思
這一問題主要是因為對於字元串開頭可能存在的字元考慮不全。在後面修改狀態機時,我在每個狀態都排查了所有合法輸入的可能,確保了狀態機的正確性。每行代碼都需要推敲與證明。
運算
運算主要是對於一個多項式完成加、減、乘、求導等操作。由於已經經過輸入部分的處理,因此不必在考慮非法輸入的問題,只需要對合法多項式進行對應操作即可。這部分的難度較低,但由於 \(Poly\) 類和 \(Item\) 類的底層數據結構均為集合,涉及到了拷貝問題,還是引發了一些問題。
淺拷貝
淺拷貝問題發生在構造新對象時。這一問題不僅存在於 \(Item\) 類和 \(Poly\) 類中,還存在於 \(Factor\) 類和 \(Element\) 子類中。由於構造方法中簡單的進行賦值,就造成了多個對象中的屬性指向同一個元素。操作一個對象時會改變其他對象的值。
位置
所有類的構造方法。
樣例輸入
記不清了…
解決方法
我最開始的解決方法是調用者負責 \(clone\) ,但構造函數一多,這樣的解決辦法很容易出錯。因此我後來將 \(clone\) 的調用轉移到構造方法中,雖然增加了複雜度,但代碼更加簡潔。
反思
這一問題的出現讓我直接把 \(Element\) 和 \(Factor\) 改造成了不可變對象,每次調用其方法時必須申請新變數。這樣的措施雖然有效,卻沒有根除問題。事實上,這一問題在作業 \(3\) 的整個開發過程中一直存在,直到提交前才被解決。這幾乎是本項目設計上最嚴重的問題,應該從構架時著手思考。在以後項目開發的過程中,我會更加留意深淺拷貝的問題。
可變類型與不可變類型
在第三次作業中,由於出現了因數的嵌套,可變性的問題才顯得尤其突出。儘管我在編碼時儘量把類構造成不可變對象,且每個類都顯式重寫了 \(Object.equals(Object)\) 方法。但 \(Item\) 類與 \(Poly\) 類的構造方法中調用了本類的 \(mult()\) 和 \(add()\) 方法,因而不能完全構造成不可變對象。對這一問題,我的解決方法是構造私有的 \(mult()\) 和 \(add()\) 方法,供類內部使用。而外部調用 \(mult()\) 和 \(add()\) 方法時通過公共方法 \(mult(Derivable)\) 和 \(add(Derivable)\) 獲得新對象。這樣在類的內部,\(Item\) 類與 \(Poly\) 類是可變類型對象;在類的外部,\(Item\) 類與 \(Poly\) 類仿佛是不可變對象。但這決定了在 \(Item\) 類和 \(Poly\) 類的內部可能存在可變類型與不可變類型混淆的情況。
位置
\(Item.mult\) 方法(由於 \(Debug\) 過程較為複雜,具體哪個重載方法記不清了…)
樣例輸入
sin(sin(x))錯誤輸出:
cos(sin(x))解決方法
該問題的解決並不困難,只要定位到 \(Bug\) 並將返回值(新對象)賦值即可。難點主要在於 \(Bug\) 定位,因為帶嵌套的表達式會進入遞歸。我採取的是二分定位的方法,將程式分成若幹片段,在每個遞歸程式間設置斷點,定位到程式片之後再進入遞歸跟蹤斷點。
反思
這一問題是由於 \(Item\) 類和 \(Poly\) 類的可變性引起的。我在編碼時就預感到這樣的設計可能導致 \(Bug\) ,但還是沒有將所有情況考慮完備。如果將 \(Item\) 類和 \(Poly\) 類完全設計為可變類型,雖然在調用者處需要顯式調用 \(clone\) 方法,但卻解決了類型可變性的問題。只是這樣的修改成本較大,在後期我沒有採用這樣的方法。
輸出
輸出部分的難點集中在判斷和調用子類的 \(toString()\) 方法。比如一個 \(Item\) 類包含兩個 \(Factor\) ,\(1\) 和 \(x^2\) 。應輸出 \(+x^2\) ,但單獨調用每個 \(Factor\) 的 \(toString()\) 方法並拼接將會生成 \(+1*x^2\) 。由此可知,輸出的問題可能出現在優化中。
表達式因數的優化
在優化作業 \(3\) 時,由於涉及到合併同類項,\(Item\) 類的輸出會包含表達式因數。這是一個十分複雜的過程,因為表達式因數的括弧在某些情況下是可以省略的(如果表達式因數只有一個 \(Factor\))。問題出現在表達式因數的第一項包含省略時,即形如 \(+x^2\) 的情況。若表達式因數的括弧被省略,那麼在這個 \(Item\) 中將會出現非第一項被省略的情況,即形如 \(4*x^5*+sin(x)\) 。
位置
\(Item.toString()\)
樣例輸入
不考慮求導過程,即調用
System.out.println(new PolyBuild(string).parsePoly())時,若輸入
4*x^5*5*sin(x)-4*x^5*4*sin(x)將會產生輸出:
4*x^5*+sin(x)解決方法
在合併同類項時,加入判斷表達式因數是否可以轉發為其他因數。若表達式因數只含一個 \(Item\) ,則將其轉化為 \(Item\) 與本類相乘。
反思
為了使優化更加簡單,不易出錯,應將優化過程前移至最開始可以優化的位置。以合併同類項為例,在項與表達式因數相乘時即可開始優化。如果在運算完成後在進行優化,一方面需要訪問多個類的私有方法,破壞了封裝性;另一方面操作過於複雜,容易引發錯誤。
互測策略
一般來說,我測試其他人代碼分為三個步驟:
- 利用針對自己代碼的測試集進行測試
- 閱讀代碼,針對性測試
- 利用腳本大量測試
測試集測試
一般情況下,這種測試方法只能檢查程式的基本表現。由於測試集是針對我的代碼編寫的,儘管從我的編碼邏輯上做到了覆蓋,但並不一定能覆蓋他人的代碼。因此這一輪測試只是檢查他人代碼能否完成最基本的求導操作。
針對性測試
這個階段我會閱讀對方代碼。閱讀重點放在輸入和輸出的處理,因為運算部分比較簡單。如果有比較明顯的邏輯錯誤,在這個階段就可以暴露出來。如果閱讀一遍沒有發現問題,我會查看運算部分的邏輯,同時編寫測試集進行測試。但是這裡的測試集一般不能做到覆蓋,只是針對頂層的邏輯進行檢查,否則沒有時間測試更多代碼。
腳本測試
腳本測試一般和閱讀代碼同時進行,因為測試量較大,運行時間長( \(5000\) 個測試樣例一般需要 \(15\sim20\) 分鐘)。如果前兩個階段都沒有發現問題,腳本生成的隨機輸入可以全面檢查程式的正確性。大部分 \(Bug\) 都會在這個階段被髮現。
Creational Pattern
在開始寫這一單元項目的時候,我對設計模式還沒有很全面的瞭解,因此沒有運用。但後來查閱相關資料發現原型模式很適合我的項目。由於我的所有類都繼承自 \(Derivable\) 介面,而且所有類都重寫了 \(clone\) 方法(由於 \(Derivable\) 介面繼承了 \(Cloneable\) 介面,因此必須重寫)。我認為重構可以在 \(Derivable\) 介面中加入預設的 \(clone\) 方法,並子類的構造方法融入 \(clone\) 方法中。這樣不僅可以加快程式的運行速度,還能更嚴格的保證對象的不可變性。
(\(P.S.\) 不知道 Applying Creational Pattern 是不是設計模式的意思…)


