1.二維數組中的查找 在一個二維數組中(每個一維數組的長度相同),每一行都按照從左到右遞增的順序排序,每一列都按照從上到下遞增的順序排序。請完成一個函數,輸入這樣的一個二維數組和一個整數,判斷數組中是否含有該整數。 時間限制:1秒 空間限制:32768K 分析:由於每一行都按照從左到右遞增的順序排序 ...
1.二維數組中的查找
在一個二維數組中(每個一維數組的長度相同),每一行都按照從左到右遞增的順序排序,每一列都按照從上到下遞增的順序排序。請完成一個函數,輸入這樣的一個二維數組和一個整數,判斷數組中是否含有該整數。
時間限制:1秒 空間限制:32768K
分析:由於每一行都按照從左到右遞增的順序排序,每一列都按照從上到下遞增的順序排序,所以右上角的數字就是該行的最大值,該列的最小值。則可以通過把目標數與右上角的數字比較來判斷其位置,如果目標數比該數字小,由該數字為該列的最小值可得這一列都不會有目標數,我們就可以將該列刪除,並得到新的二維數組,再次比較目標數與右上角的數字的大小關係。如果目標數比該數字大,由該數字為該行的最大值可得這一行都不會有目標數,我們就可以將該行刪除,並得到新的二維數組,再次比較目標數與右上角的數字的大小關係。如果目標數與右上角的數字相等,則返回true,找到了該目標數。如果當行數和列數都被刪完了還沒找到,則該二維數組中就沒有該目標數。
function Find(target, array) { if(array==undefined||array.length<0||array[0].length<0){ return false; } let rows=array.length; let columns=array[0].length; let row=0; let column=columns-1; while(row<rows&&column>=0){ if(array[row][column]==target){ return true; } if(array[row][column]>target){ column--; }else{ row++; } } return false; }
2.替換空格
請實現一個函數,將一個字元串中的每個空格替換成“%20”。例如,當字元串為We Are Happy.則經過替換之後的字元串為We%20Are%20Happy。
時間限制:1秒 空間限制:32768K
分析:這裡用replace+正則表達式即可替換。
function replaceSpace(str) { return str.replace(/ /g,'%20') }
3.從頭到尾列印鏈表
輸入一個鏈表,按鏈表值從尾到頭的順序返回一個ArrayList。鏈表節點如下:
function ListNode(x){ this.val = x; this.next = null; }
時間限制:1秒 空間限制:32768K
分析:首先我們應該判斷鏈表是否存在,如果鏈表存在的話,就用一個迴圈來判斷節點是否存在,依次將節點中的值放入棧(題目要求從尾到頭的順序)即可。
function printListFromTailToHead(head) { if(head==undefined) { return 0; }else { var arr=new Array(); var curr=head; while(curr) { arr.push(curr.val); curr=curr.next; } return arr.reverse(); } }
4.重建二叉樹
輸入某二叉樹的前序遍歷和中序遍歷的結果,請重建出該二叉樹。假設輸入的前序遍歷和中序遍歷的結果中都不含重覆的數字。例如輸入前序遍歷序列{1,2,4,7,3,5,6,8}和中序遍歷序列{4,7,2,1,5,3,8,6},則重建二叉樹並返回。樹節點如下:
function TreeNode(x) { this.val = x; this.left = null; this.right = null; }
時間限制:1秒 空間限制:32768K
分析:首先我們要知道前序遍歷的順序是根左右,中序遍歷的順序是左根右。前遍歷的第一個數總是根,所以我們就可以在前序遍歷中先找到根,再在中序遍歷中分別找到左子樹和右子樹,然後再分別在左子樹和右子樹中按照相同的方法去找它們的根節點,左右子樹,直到在某個子樹中的前序和後序遍歷的長度都為0。由此我們可以寫出如下的遞歸代碼:
function reConstructBinaryTree(pre, vin) { if(pre.length==0&&vin.length==0) { return null; } var index=vin.indexOf(pre[0]); var left=vin.slice(0,index); var right=vin.slice(index+1); var root=new TreeNode(pre[0]); root.left=reConstructBinaryTree(pre.slice(1,index+1),left); root.right=reConstructBinaryTree(pre.slice(index+1),right); return root; }
5.用兩個棧實現隊列
用兩個棧來實現一個隊列,完成隊列的Push和Pop操作。 隊列中的元素為int類型。
時間限制:1秒 空間限制:32768K
分析:首先我們要明白棧的特點是後進先出,隊列的特點是先進先出。這裡我們可以用棧stack1壓入隊列,不做特殊處理,就用棧的方法壓入。再在另一個用於Pop的方法中,把stack1中數依次彈出並壓入棧stack2,這樣就滿足了最先進入棧stack1在棧stack2的棧頂,由於Pop操作每次只彈出一個值,所以需要彈出stack2的棧頂值,用一個變數存起來,然後再把stack2中數依次彈出並壓入棧stack1,以便下次正常壓入彈出,最後返回變數即可。
var stack1=new Array(); var stack2=new Array(); function push(node) { stack1.push(node); } function pop() { var temp=stack1.pop(); while(temp){ stack2.push(temp); temp=stack1.pop(); } var result=stack2.pop(); temp=stack2.pop(); while(temp){ stack1.push(temp); temp=stack2.pop(); } return result; }
6.旋轉數組的最小數字
把一個數組最開始的若幹個元素搬到數組的末尾,我們稱之為數組的旋轉。 輸入一個非減排序的數組的一個旋轉,輸出旋轉數組的最小元素。 例如數組{3,4,5,1,2}為{1,2,3,4,5}的一個旋轉,該數組的最小值為1。 NOTE:給出的所有元素都大於0,若數組大小為0,請返回0。
時間限制:3秒 空間限制:32768K
分析:這道題可以用二分法來做,但是會出現超時,所以用js的Math.min.apply(null,arr)方法來求是最高效的。
function minNumberInRotateArray(rotateArray) { if(rotateArray.length==0){ return 0; } return Math.min.apply(null,rotateArray); }
7.斐波那契數列
大家都知道斐波那契數列,現在要求輸入一個整數n,請你輸出斐波那契數列的第n項(從0開始,第0項為0)。n<=39
時間限制:1秒 空間限制:32768K
分析:斐波那契數列指的是這樣一個數列 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233,377,610,987,1597,2584,4181,6765,10946,17711,28657,46368........這個數列從第3項開始,每一項都等於前兩項之和。解決斐波那契數列可以使用遞歸的解法,但是這個卻不是最優解,因為遞歸會產生很多重覆的計算。為避免重覆計算,我們可以根據f(0)和f(1)算出f(2),再根據f(1)和f(2)算出f(3)......依次類推就可以算出第n項了。
function Fibonacci(n){ if(n<0||n>39){ return; } if(n==0){ return 0; } if(n==1){ return 1; } var fibNMinusOne=0; var fibNMinusTwo=1; var fibN=0; for(var i=2;i<=n;i++){ fibN=fibNMinusOne+fibNMinusTwo; fibNMinusOne=fibNMinusTwo; fibNMinusTwo=fibN; } return fibN; }
8.跳臺階
一隻青蛙一次可以跳上1級臺階,也可以跳上2級。求該青蛙跳上一個n級的臺階總共有多少種跳法(先後次序不同算不同的結果)。
時間限制:1秒 空間限制:32768K
分析:首先我們考慮最簡單的情況。如果只有1級臺階,那顯然只有一種跳法。如果有2級臺階,那就有兩種跳法:一種是分兩次跳,每次跳1級;另一種就是一次跳2級。接著我們再來討論一般情況。我們把n級臺階時的跳法看成n的函數,記為f(n)。當n>2時,第一次跳的時候就有兩種不同的選擇:一次第一次只跳1級,此時跳法數目等於後面剩下的n-1級臺階的跳法數目,即為f(n-1);二是第一次跳2級,此時跳法數目等於後面剩下的n-2級臺階的跳法數目,即為f(n-2)。因此,n級臺階的不同跳法的總數f(n)=f(n-1)+f(n-2)。這實際上就是斐波那契數列。
function jumpFloor(number){ if(number <= 0){ return 0; } if(number == 1){ return 1; } if(number == 2){ return 2; } var jumpNMinusOne=1; var jumpNMinusTwo=2; var jumpN=0; for(var i=3;i<=number;i++){ jumpN=jumpNMinusOne+jumpNMinusTwo; jumpNMinusOne=jumpNMinusTwo; jumpNMinusTwo=jumpN; } return jumpN; }
9.變態跳臺階
一隻青蛙一次可以跳上1級臺階,也可以跳上2級……它也可以跳上n級。求該青蛙跳上一個n級的臺階總共有多少種跳法。
時間限制:1秒 空間限制:32768K
分析:首先我們考慮最簡單的情況。如果只有1級臺階,那顯然只有一種跳法。如果有2級臺階,那就有兩種跳法:一種是分兩次跳,每次跳1級;另一種就是一次跳2級。如果只有3級臺階,那就有4種跳法:①分三次跳,每次跳1級;②分二次跳,第一次跳2級第二次跳1級;③分二次跳,第一次跳1級第二次跳2級;④分一次跳,直接跳3級。接著我們再來討論一般情況。我們把n級臺階時的跳法看成n的函數,記為f(n)。當n>1時,第一次跳的時候就有n種不同的選擇:第一次只跳1級,此時跳法數目等於後面剩下的n-1級臺階的跳法數目,即為f(n-1);第一次跳2級,此時跳法數目等於後面剩下的n-2級臺階的跳法數目,即為f(n-2);同理第一次跳n-1級,此時跳法數目等於後面剩下的1級臺階的跳法數目,即為f(1);第一次跳n級,此時跳法數目等於後面剩下的0級臺階的跳法數目,即為f(0)也就是0次。因此,n級臺階的不同跳法的總數f(n)=f(n-1)+f(n-2)+...+f(0)。又因f(n-1)=f(n-2)+f(n-3)+...+f(0)。所以f(n)=2*f(n-1)。
function jumpFloorII(number) { if(number <= 0){ return 0; } if(number == 1){ return 1; } var jumpNMinus=1; var jumpN=0; for(var i=2;i<=number;i++){ jumpN=jumpNMinus*2; jumpNMinus=jumpN; } return jumpN; }
10.矩形覆蓋
我們可以用2*1的小矩形橫著或者豎著去覆蓋更大的矩形。請問用n個2*1的小矩形無重疊地覆蓋一個2*n的大矩形,總共有多少種方法?
時間限制:1秒 空間限制:32768K
分析:
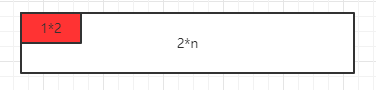

我們討論一般情況。我們把放的方法的看成n的函數,記為f(n)。當第一個小矩形這樣橫著放時,剩下的放法即為f(n-2)。

當第一個小矩形這樣豎著放時,剩下的放法即為f(n-1)。由此我們可以得到f(n)=f(n-1)+f(n-2),所以這個問題其實還是斐波那契數列。
function rectCover(number) { if(number==1){ return 1; } if(number==2){ return 2; } var rectNMinusOne=1; var rectNMinusTwo=2; var rectN=0; for(var i=3;i<=number;i++){ rectN=rectNMinusOne+rectNMinusTwo; rectNMinusOne=rectNMinusTwo; rectNMinusTwo=rectN; } return rectN; }



