————看,他已經敲了三次OO作業,精神仍然很好 1. 類的設計反思 筆者三次OO作業,每次都為如何設計類與類間關係而頭痛,回顧三次痛苦經歷,總結出如下原因: 分類不是源於需求而是拘泥於問題的錶面形式。 以第二、三次作業為例,我們將多項式拆分為單項式,繼而拆分為因數,卻難以給出如此拆分的理由。當我們 ...
————看,他已經敲了三次OO作業,精神仍然很好
1. 類的設計反思
筆者三次OO作業,每次都為如何設計類與類間關係而頭痛,回顧三次痛苦經歷,總結出如下原因:
分類不是源於需求而是拘泥於問題的錶面形式。
以第二、三次作業為例,我們將多項式拆分為單項式,繼而拆分為因數,卻難以給出如此拆分的理由。當我們面對拆分之後的因數時,卻發現求導方式需要分類討論,降低了類內聚性。所謂使用介面也正是由於目前項目架構不完全面向於需求而採取的折衷做法。
因此,我們不妨換種思維方式,從求導法則的角度出發,尋找在求導過程中有相同行為的元素歸為一類。

原需求中求導法關係法則有以上三條:由加法法則我們可以發現所有由正負號連接的元素在求導時行為相同,這解釋了我們Polynomial中拆分Monomial類的原因,同理,可以將所有乘法相連的元素歸為一類,這解釋了我們Monomial中拆分Factor類的原因。對於鏈式法則,我們不妨將題目中可能出現的sin(.*)與cos(.*)均當作複合函數看待,這將簡化因數類中遞歸終點處情況的討論。(當然這都感激求導法則與多項式構造原則存在一定的對應關係)
2. 基於度量來分析自己的程式結構
Homework1:

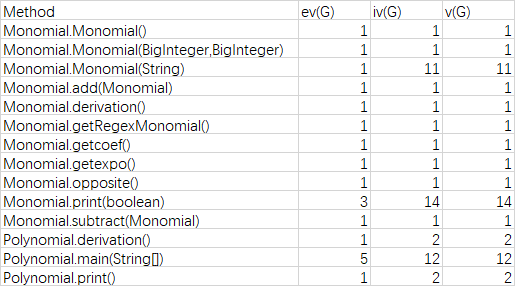
Homework2:


Homework3:


比較遺憾的是由於礙於設計原因這三次作業都沒能使用繼承方法減小類的長度,以致於最後的Factor仍然十分臃腫。
3.分析自己程式的bug
最嚴重的bug並沒有被測出,觀察以下兩個正則表達式最後幾個字元:
1 String seperator_wrong = 2 "(?<=[0-9x)]\\s{0,60})(?<sign>\\*)(?=\\s*[0-9xsc(-+])"; 3 String seperator_right = 4 "(?<=[0-9x)]\\s{0,60})(?<sign>\\*)(?=\\s*[0-9xsc(+-])";
發現只有最後的+-的位置是反的,但是字元集中的‘-’字元會優先解釋為表示字元區間的連接符,這將會導致兩個正則表達式意義截然不同。當大家[+-]寫習慣之後這個bug極難發現。當然‘-’這種特殊字元在IDE中會變色,所以還是轉義比較穩妥。
4.分析自己發現別人程式bug所採用的策略
除了傳統的邊界情況測試之外,我主要從構建多項式方式入手:
首先瞭解到建立多項式的方式主要為兩種,一種是寫出下層元素表達式從上層字元串一點一點拆分,另一種是從上層表達式中找到分割字元直接傳入下層表達式。對於第一種方法主要考察迴圈首末處可能出現的錯誤(如多符號“x*sin(x)*”),第二種方法主要考察其尋找分割字元時的準確程度(如在分割字元周圍插入非法字元等)
至於第三次作業中同學輸出普遍較長,利用matlab測試腳本輔助,核心代碼如下:
Expected = double(subs(diff(str2sym(Inputl)),'x', a(i))); #註意str2sym只於2017b版本以上適用



