一、程式設計思路 在我的三次作業中都採用了類的分層結構,採用逐項匹配,分層求導的思路。 (一)、 第一次作業中構建了Polynimial(多項式)類,在類的構造器中就完成了對非法空格的判斷並對合法表達式進行刪除空格處理。由於第一次作業僅含有帶有繫數的冪函數與常數項,因而我就沒有專門構建針對每一個項的 ...
一、程式設計思路
在我的三次作業中都採用了類的分層結構,採用逐項匹配,分層求導的思路。
(一)、
第一次作業中構建了Polynimial(多項式)類,在類的構造器中就完成了對非法空格的判斷並對合法表達式進行刪除空格處理。由於第一次作業僅含有帶有繫數的冪函數與常數項,因而我就沒有專門構建針對每一個項的類,而是在本類中就定義了getitem方法,用正則表達式逐項匹配出符合要求的項。在第一次作業中我求導的基本單位為項,在構造正則表達式時我對錶達式中可能出現項的類型進行枚舉,分別為:(1)繫數與指數均有的冪函數,(2)僅有繫數的冪函數,(3)僅有指數的冪函數,(4)無指數,無繫數的冪函數(x),(5)僅為常數;每一次調用getitem方法時,從表達式開頭按順序尋找符合要求的項,將它摳出來並分別進行求導操作,逐項輸出返回至main函數所在類。併在main函數所在類中完成合併同類項、化簡輸出的操作。
(二)、
第二次作業較第一次作業增加了三角函數因數,並且改變了項中因數的構造。在第一次作業中可以視為冪函數的繫數的常數因數,在第二次作業中必須作為一個單獨的因數來處理。比如在第一次作業中僅會出現3*x^2類型的項,這時其中的繫數“3”可以看作是3*x^2冪函數的一部分,與冪函數合併處理,而在第二次作業中可能會出現3*3*x^2這種類型的項,這時若將第一個”3“當作常數因數來處理,將第二個”3“仍然當作冪函數的繫數來處理,整個類的構造就顯得拖沓、臃腫,因此我將這個項中的兩個”3“均當作一個常數因數來處理,即為取消了第一次作業中的帶有繫數的冪函數因數,在第二次作業中的冪函數僅有x與x^n兩種。為了簡化第二次作業的設計,在第二次作業中我設計的求導方法的基本單位仍然為項,這也為第三次作業埋下了先天缺陷。同樣地,在第二次作業中,我也採用了逐項匹配的思路。我構造了一個針對每一項的正則表達式:
1 String itemregex = 2 "([-+]?)" + "(" + // 正負號 用於連接item 3 "(\\*(sin|cos)\\(x\\)\\^[-+]?\\d+)|" + // 因數5 有指數的正弦函數 4 "(\\*(sin|cos)\\(x\\))|" + // 因數4 無指數的正弦函數 5 "(\\*x\\^[-+]?\\d+)|" + // 因數3 有指數的冪函 6 "(\\*x)|" + // 因數2 無指數的冪函數 7 "(\\*[-+]?\\d+)" + // 因數1 帶符號整數 8 ")+";
可以看出,每一項均由以”*“為開頭的5種因數構成,但是在每一項的開頭那個因數,比如3*3*x^2這個項中的第一個帶符號整數因數”3'的前面並沒有“*”,這種情況怎麼將第一個因數匹配進去呢?
在這裡面我想說明我處理開頭因數時的一個小trick。根據指導書上的文法介紹,每一項的開頭可能有1個、2個、3個連續的正負號。當開頭有三個連續符號時,緊接著的因數必須是常數。在Polynomial類中我設計了一個modifybegin的方法,第一步,當表達式開頭無符號,則添上一個正號;當表達式開頭有三個符號時,將前兩個符號等價處理為一個符號;當表達式開頭有兩個符號時,若第三個字元是數字,則不處理,若第三個字元不為數字,則將前兩個符號合併;當表達式開頭只有一個符號,不處理。第二步,在表達式的第一個符號後面塞進去一個”*“。這樣,若一個含有兩個因數表達式為“+++1*+1,++x*+1,++1*+1,+1*+1,”,第一步處理完為“++1*+1,+x*+1,++1*+1,+1*+1”,第二步處理完為“+*+1*+1,+*x*+1,+*+1*+1,+*1*+1”。我們可以把處理表達式理解為,第一個乘號前面的正負號為連接符,第一個乘號後面的正負號為帶符號整數的符號。可以看出,經過處理的表達式,“*”號的個數與因數個數相等,即處理了文法,避免了形似“+++1”類型項的特判,又方便了每個因數的匹配,避免了為第一個因數專門書寫正則表達式的繁瑣。這個方法我沿用到了第三次作業中。
匹配到一個項後,就進入Item類中進行求導運算,Item類以a*x^b*sin(x)^c*cos(x)^d形式來存儲每一個項,併進行求導運算,返回一個Arraylist<Biginteger[]>類型的二維數組,存儲求導後的每一項以及每一項中的abcd值,再以bcd的合併作為key在HashMap中存儲每一項,同時進行合併同類項操作,最後轉化為String類型輸出結果。
(三)
第三次作業較第二次作業增加了嵌套因數與表達式因數,雖說增添的因數的類型不多,但這也意味著不能用前兩次作業那種投機取巧方法來處理多項式了,於是我在繼承前兩次作業的Polynomial類與Item類的基礎上,花了大量時間在構造因數類上orz。
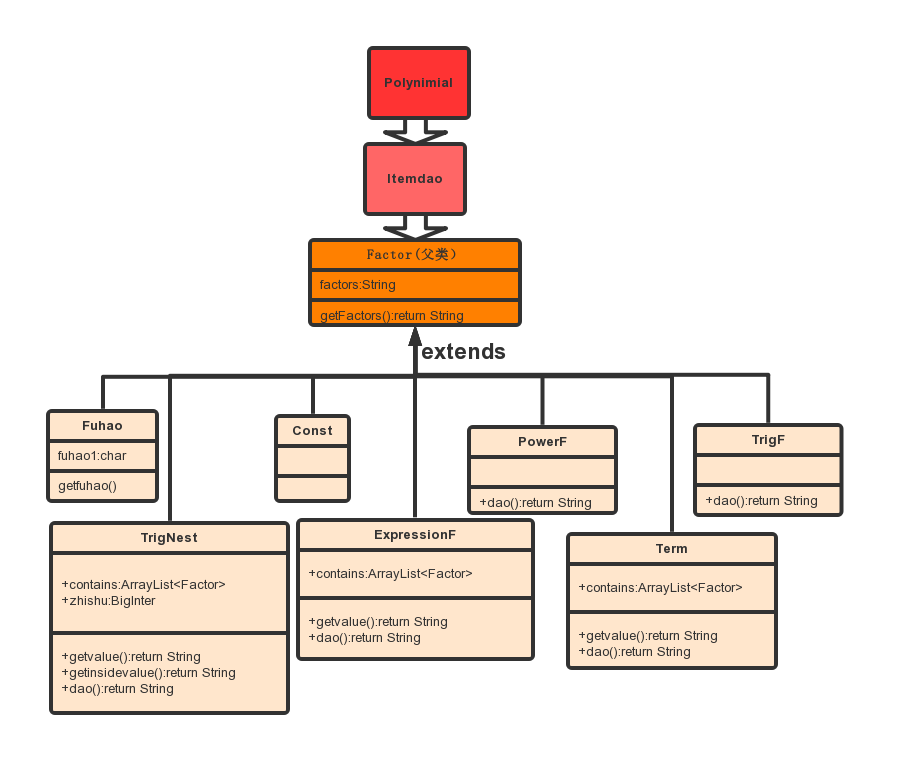
我構造了一個父類Factor,包含一個String類型的值factor與一個基本的方法getFactors(),一共7個子類全部繼承自Factor,除常數與符號類外其他類都各自定義了求導方法,兩個含有嵌套表達式的類還定義了自己的取值方法getvalue()。
| Fuhao | 存儲表達式開頭的符號 |
| Const | 存儲常數因數 |
| PowerF | 存儲表達式因數 |
| TrigF | 存儲三角函數因數 |
| TrigNest | 存儲三角函數嵌套因數的函數名與嵌套的表達式 |
| ExpressionF | 存儲表達式因數嵌套的表達式 |
| Term | 存儲嵌套表達式中的每一個項 |
同樣地,第三次作業我還是採用逐項匹配的思路,只是在第三次作業中我採用了逐因數匹配,在getitem方法中,先一個因數一個因數地匹配,匹配完一個項,返回一個名為itemfactor的Arraylist<Factor>類型數組;若匹配到了嵌套因數開頭或表達式因數開頭,則重覆調用getitem方法,在嵌套因數中繼續匹配表達式,直到遇到“)”返回,將返回的Arraylist<Factor>數組儲存到ExpressionF類或TrigNest類中的contains數組,再將ExpressionF類或TrigNest類儲存到itemfactor中,itemfactor即為這一項包含的所有因數內容,進入Itemdao類求導運算,再逐因數匹配下一個項,直到表達式完成。
ArrayList<Factor> itemfactor = new ArrayList<>(); String trigfuncregex = "\\*(sin|cos)\\(x\\)(\\^[-+]?\\d+)?"; //三角函數因數 String powerfuncregex = "\\*x(\\^[-+]?\\d+)?"; //冪函數因數 String constantregex = "\\*[-+]?\\d+"; //帶符號整數因數 String trigfuncnestregex = "\\*(sin|cos)(\\()"; //帶嵌套因數的三角函數開頭 String expressionbeginregex = "\\*(\\()"; //表達式因數開頭
在Item類中,逐項遍歷Arraylist<Factor>中的每一個Factor,調用這個Factor的求導方法與其他所有Factor的getvalue()方法,將返回值用“*”連在一起並輸出,就是針對當前項的求導結果,若遇到的是一個嵌套因數,則補上左右括弧併在內部遞歸求導,最後返回String類型的求導結果至Polynimial類中,再由Polynomial類返回至main函數輸出。
在對輸出的優化處理中,我將輸出項含有“0”因數的項直接丟棄,具體實現方法是在求導過程中,若求導後輸出結果為0(一般出現在常數求導中),則直接中斷這個for迴圈,不將針對這一項的求導結果合併到result字元串中,這樣可以避免後期處理過程中可能出現的判斷錯誤。
二、程式結構分析:

各類總代碼規模:(Statistic):
| Source File | Total Lines | Source Code ines | Comment Lines | Blank Lines |
| Fuhao.java | 17 | 13 | 0 | 4 |
| Factor.java | 17 | 13 | 0 | 4 |
| Const.java | 11 | 9 | 0 | 2 |
| ExpressionF.java | 87 | 80 | 0 | 7 |
| PowerF.java | 54 | 50 | 0 | 4 |
| Itemdao.java | 114 | 106 | 0 | 8 |
| TrigNest.java | 146 | 138 | 0 | 8 |
| Term.java | 146 | 138 | 0 | 8 |
| TrigF.java | 76 | 72 | 0 | 4 |
| Homework3main.java | 27 | 22 | 3 | 2 |
| Polynomial.java | 255 | 231 | 9 | 15 |
複雜度分析(class)[Metrics]:
| class | OCavg | WMC |
| homeworkthree.factor.Const | 1.0 | 2.0 |
| homeworkthree.factor.ExpressionF | 6.75 | 27.0 |
| homeworkthree.factor.Factor | 1.0 | 3.0 |
| homeworkthree.factor.Fuhao | 1.0 | 3.0 |
| homeworkthree.factor.PowerF | 3.3333333333333335 | 10.0 |
| homeworkthree.factor.Term | 7.333333333333333 | 44.0 |
| homeworkthree.factor.TrigF | 5.0 | 15.0 |
| homeworkthree.factor.TrigNest | 6.333333333333333 | 38.0 |
| homeworkthree.Homework3main | 3.0 | 3.0 |
| homeworkthree.Itemdao | 6.0 | 30.0 |
| homeworkthree.Polynomial | 4.166666666666667 | 50.0 |
| Total | 225.0 | |
| Average | 4.6875 | 20.454545454545453 |
複雜度分析(method)[Metrics]:
| method | ev(G) | iv(G) | v(G) |
| homeworkthree.factor.Const.Const() | 1.0 | 1.0 | 1.0 |
| homeworkthree.factor.Const.Const(String) | 1.0 | 1.0 | 1.0 |
| homeworkthree.factor.ExpressionF.dao() | 9.0 | 10.0 | 11.0 |
| homeworkthree.factor.ExpressionF.ExpressionF(ArrayList) | 1.0 | 1.0 | 1.0 |
| homeworkthree.factor.ExpressionF.getContains() | 1.0 | 1.0 | 1.0 |
| homeworkthree.factor.ExpressionF.getvalue() | 1.0 | 11.0 | 16.0 |
| homeworkthree.factor.Factor.Factor() | 1.0 | 1.0 | 1.0 |
| homeworkthree.factor.Factor.Factor(String) | 1.0 | 1.0 | 1.0 |
| homeworkthree.factor.Factor.getFactors() | 1.0 | 1.0 | 1.0 |
| homeworkthree.factor.Fuhao.Fuhao() | 1.0 | 1.0 | 1.0 |
| homeworkthree.factor.Fuhao.Fuhao(char) | 1.0 | 1.0 | 1.0 |
| homeworkthree.factor.Fuhao.getfuhao() | 1.0 | 1.0 | 1.0 |
| homeworkthree.factor.PowerF.dao() | 7.0 | 8.0 | 8.0 |
| homeworkthree.factor.PowerF.PowerF() | 1.0 | 1.0 | 1.0 |
| homeworkthree.factor.PowerF.PowerF(String) | 1.0 | 1.0 | 1.0 |
| homeworkthree.factor.Term.dao() | 4.0 | 12.0 | 16.0 |
| homeworkthree.factor.Term.fdao(Factor) | 7.0 | 7.0 | 7.0 |
| homeworkthree.factor.Term.fvalue(Factor) | 7.0 | 7.0 | 7.0 |
| homeworkthree.factor.Term.gettermContains() | 1.0 | 1.0 | 1.0 |
| homeworkthree.factor.Term.getvalue() | 1.0 | 9.0 | 14.0 |
| homeworkthree.factor.Term.Term(ArrayList) | 1.0 | 1.0 | 1.0 |
| homeworkthree.factor.TrigF.dao() | 12.0 | 9.0 | 13.0 |
| homeworkthree.factor.TrigF.TrigF() | 1.0 | 1.0 | 1.0 |
| homeworkthree.factor.TrigF.TrigF(String) | 1.0 | 1.0 | 1.0 |
| homeworkthree.factor.TrigNest.dao() | 10.0 | 15.0 | 17.0 |
| homeworkthree.factor.TrigNest.getContains() | 1.0 | 1.0 | 1.0 |
| homeworkthree.factor.TrigNest.getinsidevalue() | 1.0 | 11.0 | 16.0 |
| homeworkthree.factor.TrigNest.getvalue() | 1.0 | 4.0 | 4.0 |
| homeworkthree.factor.TrigNest.getZhishu() | 1.0 | 1.0 | 1.0 |
| homeworkthree.factor.TrigNest.TrigNest(String,ArrayList,BigInteger) | 1.0 | 2.0 | 2.0 |
| homeworkthree.Homework3main.main(String[]) | 1.0 | 4.0 | 4.0 |
| homeworkthree.Itemdao.dao() | 4.0 | 12.0 | 16.0 |
| homeworkthree.Itemdao.fdao(Factor) | 7.0 | 7.0 | 7.0 |
| homeworkthree.Itemdao.fvalue(Factor) | 7.0 | 7.0 | 7.0 |
| homeworkthree.Itemdao.Itemdao() | 1.0 | 1.0 | 1.0 |
| homeworkthree.Itemdao.Itemdao(ArrayList) | 1.0 | 1.0 | 1.0 |
| homeworkthree.Polynomial.dealsin(ArrayList,ArrayList,Matcher) | 1.0 | 4.0 | 4.0 |
| homeworkthree.Polynomial.deletespace() | 3.0 | 7.0 | 13.0 |
| homeworkthree.Polynomial.deletestr(String) | 1.0 | 1.0 | 1.0 |
| homeworkthree.Polynomial.geteachitem(ArrayList,Matcher,Matcher,Matcher,Matcher,Matcher) | 6.0 | 12.0 | 12.0 |
| homeworkthree.Polynomial.getitem() | 4.0 | 8.0 | 8.0 |
| homeworkthree.Polynomial.getlength() | 1.0 | 1.0 | 1.0 |
| homeworkthree.Polynomial.judgent(int,int) | 1.0 | 3.0 | 4.0 |
| homeworkthree.Polynomial.judgesincosbegin() | 1.0 | 6.0 | 6.0 |
| homeworkthree.Polynomial.modifybegin() | 1.0 | 13.0 | 16.0 |
| homeworkthree.Polynomial.Polynomial() | 1.0 | 1.0 | 1.0 |
| homeworkthree.Polynomial.Polynomial(String) | 1.0 | 8.0 | 8.0 |
| homeworkthree.Polynomial.sepitem() | 1.0 | 2.0 | 2.0 |
| Total | 122.0 | 221.0 | 261.0 |
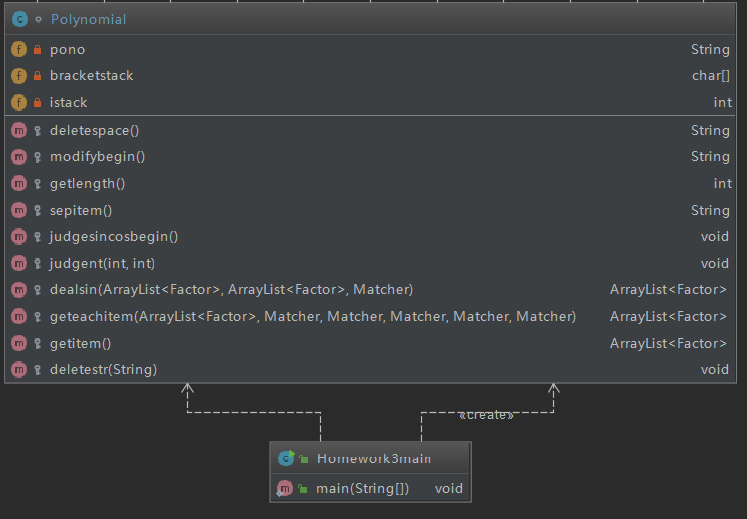
(一)、Polynomial類
| 名稱 | 規模 | |
| 屬性 | pono | 1 |
| 方法 |
sepitem |
9 |
|
deletespace |
5 |
|
|
modifybegin |
32 |
|
|
getlength |
3 |
|
|
judgesincosbegin |
12 |
|
|
judgement |
11 |
|
|
dealsin |
30 |
|
|
geteachitem |
42 |
|
|
getitem |
40 |
|
|
deletestr |
4 |
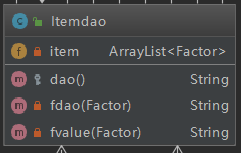
(二)、Itemdao類
| 名稱 | 規模 | |
| 屬性 | item | 1 |
| 方法 | dao | 53 |
| fdao | 17 | |
| fvalue | 17 |
(三)、package factor 中的類
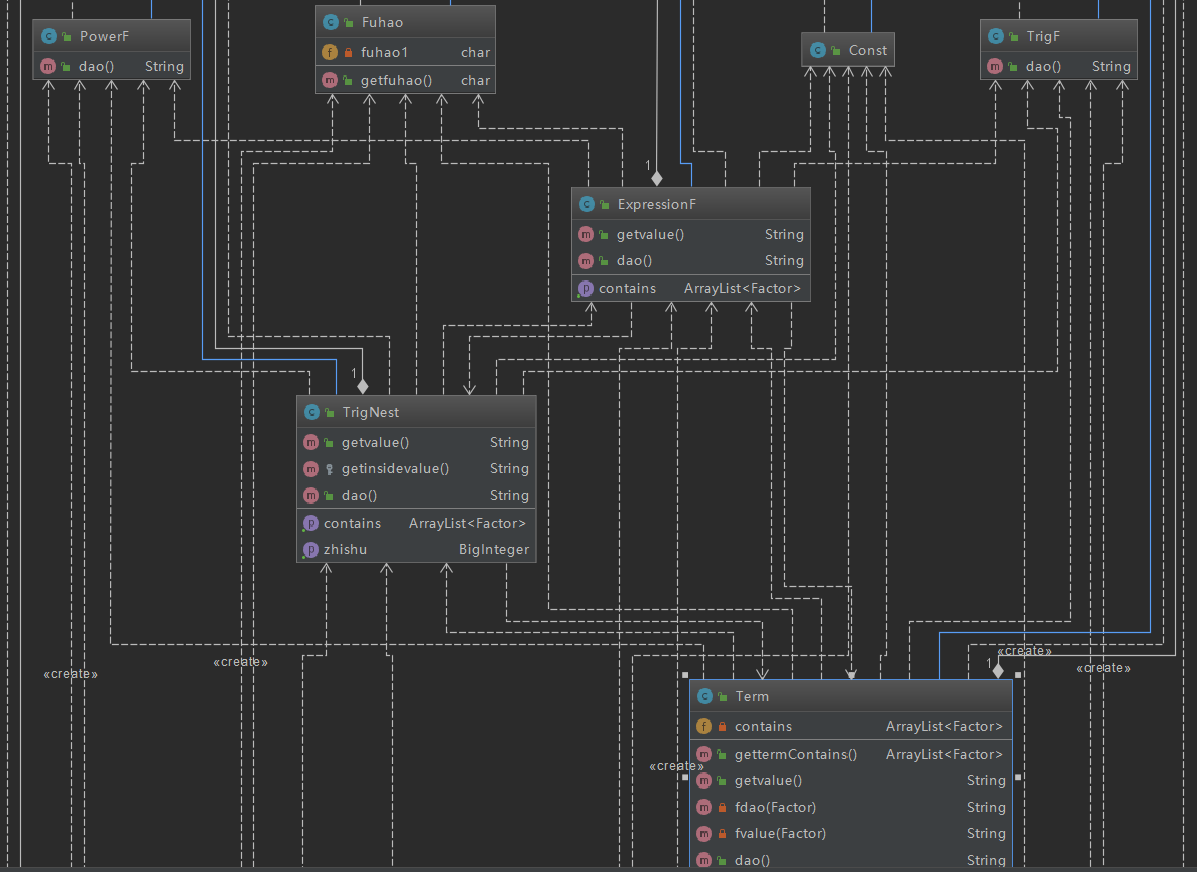
(四)、程式結構優缺點分析
優點:層次清晰,分為表達式、項、因數,共三層,僅在因數這個層次實現求導方法,易於拓展。
缺點:遞歸求導時迭代層數較多時,由於需要迭代構造幾個Term類,程式速度較慢,易出現TLE情況;
Factor層返回Item層,Item層返回Polynomial層時,由於儲存時使用的是Arraylist,而返回時需要得到String類型的value,在Arraylist向String轉化的過程中對於符號的處理易出錯,且一旦出錯,由於層次迭代較多,難以找到原因,且輸出結果也難以優化。
三、歷次作業bug分析
(一)、第一次作業
1個bug,類型:優化出錯
指數為1時輸出忽略指數,但是忘記把冪的符號"^"去掉了,,,時刻警醒
(二)、第二次作業
1個bug,類型:空格處理錯誤
對於指數中的帶符號整數的非法空格判斷,我將正則寫成了
String regex3 = "(sin\\(x\\)|cos\\(x\\)|x)"+"[\\s]*[\\^][\\s]*[+-][\\s]+[0-9]+";
這樣當sin(x)與指數的符號與數值間同時出現非法空格時無法判斷,需要修改為如下正則修複bug。
String regex3 = "[\\^][\\s]*[+-][\\s]+[0-9]+";
(三)、第三次作業
3個及以上bug,寫碼一時爽,公測火葬場。
(1)x^0以及x^1求導的bug(出現在package.factor.PowerF中)
當冪函數無指數時,我對它的求導輸出結果為1,這是對的
當冪函數有指數時,我為了簡化輸出,指數為0的時候輸出1,指數為1的時候輸出x,(第一眼看去好像沒什麼不對。
解決辦法:改了兩個字元搞定。
(2)當函數裡頭遞歸嵌套一個因數時,比如sin((x+x))這種嵌套因數求導時,我在輸出時為了優化把對內部嵌套因數輸出的括弧給去了,求導結果是cos((x+x))*(1+1),為什麼只有一層括弧呢,因為我覺得如果裡面是表達式因數,它會自帶一層括弧,我不用去考慮它。如果裡頭是一個非表達式因數,比如sin(x^2),求導完就是cos(x^2)*2*x,看起來也沒什麼不對,對吧?那麼,再難一點,如果是這樣子,sin(cos(x)),這樣輸出結果就有負號啦,會不會出事呢?看看結果,cos(cos(x))*-1*sin(x),咦?沒事兒?萬事大吉啦。(我在提交之前測試的時候就想到了這一步) 提交之後,讓我們來求一求sin((x+1))*(x+1),結果是啥?cos((x+1))*(1)*x+1+sin((x+1))*1,emmmmmmm,涼涼。
解決辦法:對於Term類的求導或者取值的輸出結果,我通通給他裹上一個括弧,優化?不存在的,(在對Term類dao()與getvalue()方法的輸出加個判斷就好了,一行搞定)
(3)CPU_TIME_LIMIT_EXCEED
(這是個神仙bug
我想說我的代碼還小,它不是不行,它只是需要時間。
在問了周圍一票人都用的什麼方法求導之後,我發現大家全是遞歸,那麼為什麼他們遞歸就那麼快呢?
於是我用debug認真一步一步跑了一下我的程式,發現是我的存儲架構的天生缺陷……前面已經說了我用的是ArrayList<Factor>存儲的每個項,遇到嵌套因數就將嵌套因數內部的表達式(因數)也存成一個ArrayList<Factor>,再將這個ArrayList存到一個嵌套因數類中,再將這個嵌套因數類存回原來的Factor,這就構成了一個鏈或者可以說是一棵樹。用ArrayList本身就已經占有了一些時間了,更奇葩的是我的存儲方式
解決辦法:我在用getitem()返回一個ArrayList後,不知道為什麼抽了又新建了一個Term類去存這個東東,這也就意味著,我嵌套因數中的每一項,都是一個Term類。這樣子結構看著舒服了,但是求導的時候,遞歸迭代層數以O(2^n)規模蹭蹭往上漲。。。跪了
為瞭解決這個bug,我為了保住我的祖傳代碼,不對結構大動干戈,我專門寫了個處理多餘括弧的方法,把外面的重括弧去了,,,這樣對於60個字元內的表達式,就很難TLE了。
四、互測尋找別人bug策略
在互測room開始前,(還不確定自己的代碼夠不夠格進room之前),我先根據之前測試自己代碼發現的bug,以及自己在代碼架構時發現的幾個易錯點,整理出一份測試代碼,上來先挑盲狙一遍。如果發現錯了,交就完事了。如果沒發現錯,就找一個長一點的測試數據,用debug模式在對方代碼上跑一遍,看下他代碼的大體思路,找找正則有沒有缺漏之初,或者一些很奇怪的地方認真琢磨一下,優秀就學習,不優秀的就叉他。
五、應用對象創建模式分析
我覺得這次三次作業中,大題對象能被分為3類:表達式、項、因數。最理想的寫法,就是在第一二次作業中就直接抽象出因數的概念,將那些用乘號隔開的字元都化為一個因數類,再項一層就可以定義求導介面,在因數那一層進行求導操作,並回溯到項一層優化並輸出,再回到表達式一層合併同類項並輸出。如果第一次作業開始就有構造因數層的類,第二次與第三次作業僅僅只是豐富了類的數目而已,連求導方法都是已經定義了的,就可以大大簡化第三次代碼的工作量,但是,早知如此,何必當初吶……



