DES詳解（Java實現）

来源:https://www.cnblogs.com/mx-lqk/archive/2019/01/15/10255149.html
-Advertisement-
Play Games

GitHub DES 數據加密標準（Data Encryption Standard），簡稱DES，是由IBM公司提交，美國政府於1977年1月5日頒佈的一種加密演算法。 DES的設計目標是，用於加密保護靜態存儲和傳輸通道中的數據，安全使用10~15年。 DES綜合運用了置換、代替、代數等多種密碼技術 ...


GitHub

DES

　　數據加密標準（Data Encryption Standard），簡稱DES，是由IBM公司提交，美國政府於1977年1月5日頒佈的一種加密演算法。

　　DES的設計目標是，用於加密保護靜態存儲和傳輸通道中的數據，安全使用10~15年。

　　DES綜合運用了置換、代替、代數等多種密碼技術。它設計精巧、實現容易、使用方便，堪稱是適應電腦環境的近代分組密碼的一個典範。DES的設計充分體現了Shannon所闡述的設計密碼的思想，標志著密碼的設計與分析達到了新的水平。

　　DES是一種分組密碼。明文、密文和密鑰的分組長度都是64位。

　　DES是面向二進位的密碼演算法。因而能夠加解密任何形式的電腦數據。

　　DES是對合運算，因而加密和解密共用同一演算法，從而使工程實現的工作量減半。

　　DES的密碼結構屬於Feistel結構。

Feistel結構

　　Feistel結構是IBM的密碼專家Horst Feistel最早提出的。由於它是對稱的密碼結構，所以對信息加密和解密的過程就極為相似，甚至完全一樣。這就使得在實施的過程中，對編碼量和線路傳輸的要求就減少了幾乎一半。

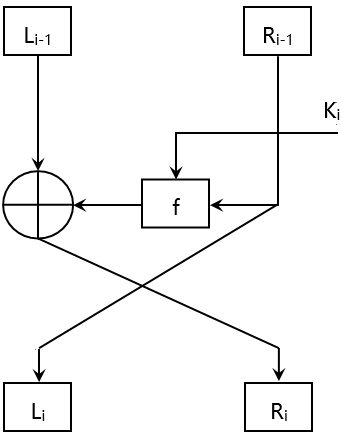
加密結構

　　Li = Ri-1

　　Ri = Li-1 ⊕ f ( Ri-1 , ki )

　　

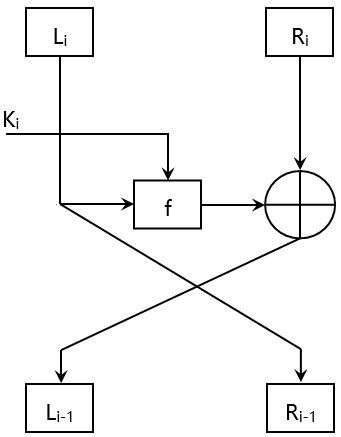
解密結構

　　Li-1 = Ri ⊕ f ( Li , ki )

　　Ri-1 = Li

　　

影響因素

　　影響Feistel結構的因素有以下5個：

　　1.塊的大小：大的塊會提高加密的安全性，但是會降低加密、解密的速度；

　　2.密鑰的大小：大的密鑰也會提高加密的安全性，但是也會降低加密、解密的速度；

　　3.輪次數：每多進行一輪迴圈，安全性就會有所提高；

　　4.子密鑰的生成演算法：生成演算法越複雜，則會使得密文被破譯的難度增強，即信息會越安全；

　　5.輪函數的複雜度：輪函數越複雜，則安全性會越高。

DES演算法細節

子密鑰的產生

　　64位密鑰經過置換選擇1、迴圈左移、置換選擇2等變換，產生出16個48位長的子密鑰。

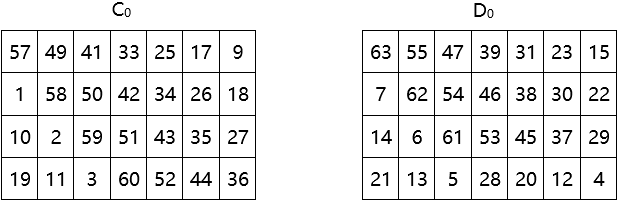
（1）置換選擇1

　　64位密鑰分為8個位元組。每個位元組的前7位是真正的密鑰位，第8位是奇偶校驗位。奇偶校驗位可以從前7位密鑰位計算得出，不是隨機的，因而不起密鑰的作用。因此，DES真正的密鑰只有56位。

　　置換選擇1的作用有兩個：一是從64位密鑰中去掉8個奇偶校驗位；二是把其餘56位密鑰位打亂重排，且將前28位作為C0，後28位作為D0。

　　置換選擇1的矩陣如下：

　　

（2）迴圈左移

　　每一次迭代，將Ci-1和Di-1按照一定的位數迴圈左移分別得到Ci和Di。

　　迴圈左移位數表如下：

　　

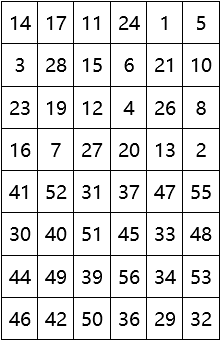
（3）置換選擇2

　　將Ci和Di合併成一個56位的中間數據，置換選擇2從中選擇出一個48位的子密鑰Ki。

　　置換選擇2的矩陣如下：

　　

初始置換IP

　　初始置換IP（Initial Permutation）的作用在於將64位數據打亂重排，並分成左右兩半，供後面的迭代使用。

　　初始置換IP的矩陣如下：

　　

輪函數

　　輪函數是DES的核心部分。在迭代中將32位的數據組A進行選擇運算E、模2相加、代替函數組S、置換運算P等運算，得到32位輸出結果。根據Shannon用混淆和擴散設計密碼的理論，DES的S盒用來提供混淆，而P置換用來提供擴散。

（1）選擇運算E

　　選擇運算E對32位的數據組A的各位進行選擇和排列，產生一個48位的結果。

　　選擇運算E是一種擴展運算，通過重覆選擇某些數據位來達到數據擴展的目的。

　　選擇運算E的矩陣如下：

　　

（2）模2相加

　　將選擇運算E得到的結果與48位子密鑰K進行模2相加，即逐位異或，得到一個48位的結果。

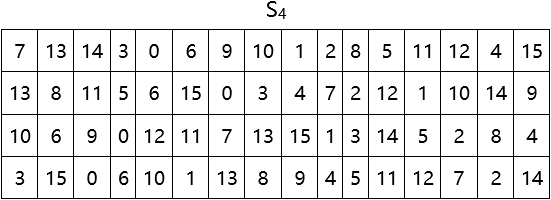
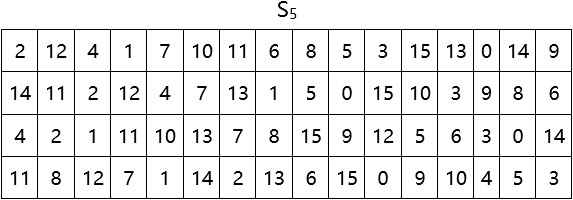
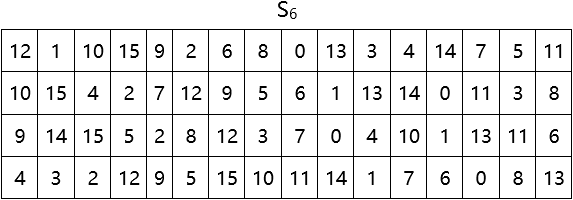
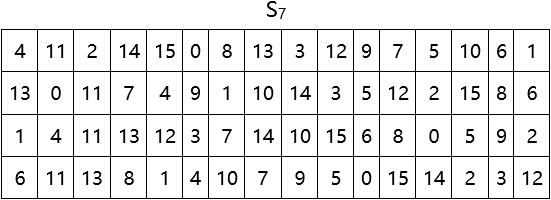
（3）代替函數組S

　　代替函數組S由8個代替函數（S盒）組成。代替函數組S的輸入是一個48位的數據，從第1位到第48位依次加到8個S盒的輸入端，即第i位到第8i位加到Si (i = 1,2,3,4,5,6,7,8)的輸入端。

　　每個S盒有一個代替矩陣，規定了其輸出與輸入的代替規則。代替矩陣有4行（0~3）16列（0~15），64個位置都是0~15這16個數字。每個S盒有6位輸入，產生4位輸出。S盒運算的結果是用輸出數據代替了輸入數據，所以稱其為代替函數。

　　S盒的代替規則是：S盒的6位輸入b1b2b3b4b5b6中的第1位和第6位數字b1b6組成的二進位數代表選中的行號，其餘4位數字b2b3b4b5組成的二進位數代表選中的列號，將處在行號和列號所代表的位置的數字以4位二進位形式輸出作為S盒的輸出。

　　S盒至少應滿足以下準則：

　　1.輸出不是輸入的線性和仿射函數；

　　2.任意改變輸入中的1位，輸出至少有2位發生變化；

　　3.對於任何S盒和任何輸入x，S(x)和S(x⊕001100)至少有2位不同；

　　4.對於任何S盒和任何輸入x，以及y,z∈GF(2)，S(x) ≠ S(x⊕11yz00)；

　　5.保持輸入中的1位不變，其餘5位變化，輸出中的0和1的個數接近相等。

　　代替函數組S中8個S盒的代替矩陣如下：

　　

　　

　　

　　

　　

　　

　　

　　

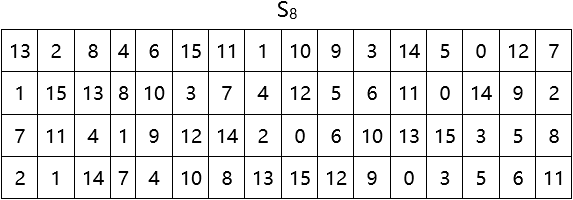
（4）置換運算P

　　置換運算P把S盒輸出的32位數據打亂重排，得到32位輪函數輸出。

　　置換運算P的矩陣如下：

　　

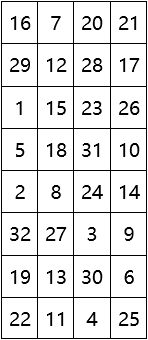
逆初始置換IP-1

　　逆初始置換IP-1是初始置換IP的逆置換。它把迭代的結果打亂重排，形成64位結果。

　　逆初始置換IP-1的矩陣如下：

　　

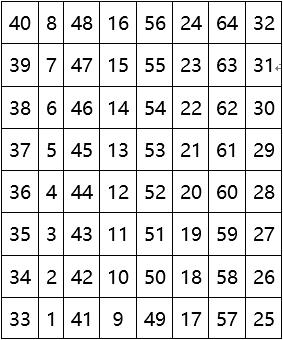
 DES的加密過程

　　1.64位密鑰經子密鑰產生演算法產生出16個48位子密鑰：K1,K2,...,K16，分別供第1次，第2次，...，第16次加密迭代使用。

　　2.64位明文首先經過初始置換IP，將數據打亂重新排列並分成左右兩半，左邊32位構成L0，右邊32位構成R0。

　　3.第i次加密迭代：由輪函數f實現子密鑰Ki對Ri-1的加密，結果為32位的數據組f ( Ri-1 , Ki )。f ( Ri-1 , Ki )再與Li-1模2相加，又得到一個32位的數據組Li-1 ⊕ f ( Ri-1 , Ki )。以Li ⊕ f ( Ri-1 , Ki )作為下一次加密迭代的Ri，以Ri-1作為下一次加密迭代的Li ( i = 1,2,...,16)。

　　4.按照上一步的規則進行16次加密迭代。

　　5.第16次加密迭代結束後，以R16為左，L16為右，合併產生一個64位的數據組。再經過逆初始置換IP-1，將數據重新排列，便得到64位密文。

DES的解密過程

　　1.64位密鑰經子密鑰產生演算法產生出16個48位子密鑰：K1,K2,...,K16，分別供第1次，第2次，...，第16次解密迭代使用。

　　2.64位密文首先經過初始置換IP，將數據打亂重新排列並分成左右兩半，左邊32位構成R16，右邊32位構成L16。

　　3.第17-i次解密迭代：由輪函數f實現子密鑰Ki對Li的解密，結果為32位的數據組f ( Li , Ki )。f ( Li , Ki )再與Ri模2相加，又得到一個32位的數據組Ri ⊕ f ( Li , Ki )。以Ri ⊕ f ( Li , Ki )作為下一次解密迭代的Li-1，以Li作為下一次解密迭代的Li-1 ( i = 16,15,...,1)。

　　4.按照上一步的規則進行16次解密迭代。

　　5.第16次解密迭代結束後，以L0為左，R0為右，合併產生一個64位的數據組。再經過逆初始置換IP-1，將數據重新排列，便得到64位明文。

DES的安全性

　　DES演算法中除了S盒是非線性變換外，其餘變換均為線性變換，所以DES安全的關鍵是S盒。因為演算法中使用了16次迭代，從而使得改變輸入明文或密鑰中的1位，密文都會發生大約32位的變化，具有良好的雪崩效應，大大提高了保密性。S盒用來提供混淆，使明文、密鑰、密文之間的關係錯綜複雜，而P置換用來提供擴散，把S盒提供的混淆作用充分擴散開來。這樣，S盒和P置換互相配合，形成了很強的抗差分攻擊和抗線性攻擊能力，其中抗差分攻擊能力更強些。

DES的安全弱點

密鑰較短

　　面對計算能力高速發展的形式，DES採用56位密鑰，顯然短了一些。如果密鑰的長度再長一些，將會更安全。

存在弱密鑰和半弱密鑰

　　弱密鑰和半弱密鑰的存在無疑是DES的一個不足。但由於弱密鑰和半弱密鑰的數量與密鑰的總數256相比仍是微不足道的，所以這並不對DES構成太大威脅，只要註意在實際應用中不使用這些弱密鑰和半弱密鑰即可。

存在互補對稱性

　　互補對稱性使DES在選擇明文攻擊下所需的工作量減半。產生互補對稱性的原因在於DES中兩次異或運算的配置，一次在輪函數中S盒之前，另一次在輪函數輸出之後。攻擊者任取一個明文M，並可得到密文C = DES ( M , K )，攻擊者只要簡單地對C取非，便得到另一明文M'（M取非）在密鑰K'（K取非）加密下的密文C' = DES ( M' , K' )。因此攻擊者只要做一次實驗便可知道K和K'是否是所求的密鑰。

Java實現

子密鑰產生

 1 //置換選擇1矩陣
 2 static int[] replace1C = {
 3         57, 49, 41, 33, 25, 17,  9, 
 4          1, 58, 50, 42, 34, 26, 18, 
 5         10,  2, 59, 51, 43, 35, 27, 
 6         19, 11,  3, 60, 52, 44, 36
 7 };
 8 static int[] replace1D = {
 9         63, 55, 47, 39, 31, 23, 15, 
10          7, 62, 54, 46, 38, 30, 22, 
11         14,  6, 61, 53, 45, 37, 29, 
12         21, 13,  5, 28, 20, 12,  4
13 };
14 
15 //迴圈左移位數表
16 static int[] moveNum = {1, 1, 2, 2, 2, 2, 2, 2, 1, 2, 2, 2, 2, 2, 2, 1};
17 
18 //置換選擇2矩陣
19 static int[] replace2 = {
20     14, 17, 11, 24,  1,  5, 
21      3, 28, 15,  6, 21, 10, 
22     23, 19, 12,  4, 26,  8, 
23     16,  7, 27, 20, 13,  2, 
24     41, 52, 31, 37, 47, 55, 
25     30, 40, 51, 45, 33, 48, 
26     44, 49, 39, 56, 34, 53, 
27     46, 42, 50, 36, 29, 32
28 };
 1 /**
 2  * 子密鑰的產生
 3  * @param sKey  64位密鑰
 4  * @return      16個48位子密鑰
 5  */
 6 static byte[][] generateKeys(byte[] sKey) {
 7     byte[] C = new byte[28];
 8     byte[] D = new byte[28];
 9     byte[][] keys = new byte[16][48];
10     //置換選擇1
11     for (int i = 0; i < 28; i++) {
12         C[i] = sKey[replace1C[i] - 1];
13         D[i] = sKey[replace1D[i] - 1];
14     }
15     for (int i = 0; i < 16; i++) {
16         //迴圈左移
17         C = RSHR(C, moveNum[i]);
18         D = RSHR(D, moveNum[i]);
19         //置換選擇2
20         for (int j = 0; j < 48; j++) {
21             if (replace2[j] <= 28) keys[i][j] = C[replace2[j] - 1];
22             else keys[i][j] = D[replace2[j] - 28];
23         }
24     }
25     return keys;
26 }
 1 /**
 2  * 迴圈左移
 3  * @param b  數組
 4  * @param n  位數
 5  * @return
 6  */
 7 static byte[] RSHR(byte[] b, int n) {
 8     String s = new String(b);
 9     s = (s + s.substring(0, n)).substring(n);
10     return s.getBytes();
11 }

初始置換IP

 1 //初始置換矩陣
 2 static int[] IP = {
 3         58, 50, 42, 34, 26, 18, 10,  2, 
 4         60, 52, 44, 36, 28, 20, 12,  4, 
 5         62, 54, 46, 38, 30, 22, 14,  6, 
 6         64, 56, 48, 40, 32, 24, 16,  8, 
 7         57, 49, 41, 33, 25, 17,  9,  1, 
 8         59, 51, 43, 35, 27, 19, 11,  3, 
 9         61, 53, 45, 37, 29, 21, 13,  5, 
10         63, 55, 47, 39, 31, 23, 15,  7
11 };
 1 /**
 2  * 初始置換IP
 3  * @param text  64位數據
 4  * @return
 5  */
 6 static byte[] IP(byte[] text) {
 7     byte[] newtext = new byte[64];
 8     for (int i = 0; i < 64; i++) 
 9         newtext[i] = text[IP[i] - 1];
10     return newtext;
11 }

輪函數

 1 //選擇運算矩陣
 2 static int[] E = {
 3         32,  1,  2,  3,  4,  5, 
 4          4,  5,  6,  7,  8,  9, 
 5          8,  9, 10, 11, 12, 13, 
 6         12, 13, 14, 15, 16, 17, 
 7         16, 17, 18, 19, 20, 21, 
 8         20, 21, 22, 23, 24, 25, 
 9         24, 25, 26, 27, 28, 29, 
10         28, 29, 30, 31, 32,  1
11 };
12 
13 //代替函數組
14 static int[][][] S = {
15         //S1
16         {
17             {14,  4, 13,  1,  2, 15, 11,  8,  3, 10,  6, 12,  5,  9,  0,  7}, 
18             { 0, 15,  7,  4, 14,  2, 13,  1, 10,  6, 12, 11,  9,  5,  3,  8}, 
19             { 4,  1, 14,  8, 13,  6,  2, 11, 15, 12,  9,  7,  3, 10,  5,  0}, 
20             {15, 12,  8,  2,  4,  9,  1,  7,  5, 11,  3, 14, 10,  0,  6, 13}
21         }, 
22         //S2
23         {
24             {15,  1,  8, 14,  6, 11,  3,  4,  9,  7,  2, 13, 12,  0,  5, 10}, 
25             { 3, 13,  4,  7, 15,  2,  8, 14, 12,  0,  1, 10,  6,  9, 11,  5}, 
26             { 0, 14,  7, 11, 10,  4, 13,  1,  5,  8, 12,  6,  9,  3,  2, 15}, 
27             {13,  8, 10,  1,  3, 15,  4,  2, 11,  6,  7, 12,  0,  5, 14,  9}
28         }, 
29         //S3
30         {
31             {10,  0,  9, 14,  6,  3, 15,  5,  1, 13, 12,  7, 11,  4,  2,  8}, 
32             {13,  7,  0,  9,  3,  4,  6, 10,  2,  8,  5, 14, 12, 11, 15,  1}, 
33             {13,  6,  4,  9,  8, 15,  3,  0, 11,  1,  2, 12,  5, 10, 14,  7}, 
34             { 1, 10, 13,  0,  6,  9,  8,  7,  4, 15, 14,  3, 11,  5,  2, 12}
35         }, 
36         //S4
37         {
38             { 7, 13, 14,  3,  0,  6,  9, 10,  1,  2,  8,  5, 11, 12,  4, 15}, 
39             {13,  8, 11,  5,  6, 15,  0,  3,  4,  7,  2, 12,  1, 10, 14,  9}, 
40             {10,  6,  9,  0, 12, 11,  7, 13, 15,  1,  3, 14,  5,  2,  8,  4}, 
41             { 3, 15,  0,  6, 10,  1, 13,  8,  9,  4,  5, 11, 12,  7,  2, 14}
42         }, 
43         //S5
44         {
45             { 2, 12,  4,  1,  7, 10, 11,  6,  8,  5,  3, 15, 13,  0, 14,  9}, 
46             {14, 11,  2, 12,  4,  7, 13,  1,  5,  0, 15, 10,  3,  9,  8,  6}, 
47             { 4,  2,  1, 11, 10, 13,  7,  8, 15,  9, 12,  5,  6,  3,  0, 14}, 
48             {11,  8, 12,  7,  1, 14,  2, 13,  6, 15,  0,  9, 10,  4,  5,  3}
49         }, 
50         //S6
51         {
52             {12,  1, 10, 15,  9,  2,  6,  8,  0, 13,  3,  4, 14,  7,  5, 11}, 
53             {10, 15,  4,  2,  7, 12,  9,  5,  6,  1, 13, 14,  0, 11,  3,  8}, 
54             { 9, 14, 15,  5,  2,  8, 12,  3,  7,  0,  4, 10,  1, 13, 11,  6}, 
55             { 4,  3,  2, 12,  9,  5, 15, 10, 11, 14,  1,  7,  6,  0,  8, 13}
56         }, 
57         //S7
58         {
59             { 4, 11,  2, 14, 15,  0,  8, 13,  3, 12,  9,  7,  5, 10,  6,  1}, 
60             {13,  0, 11,  7,  4,  9,  1, 10, 14,  3,  5, 12,  2, 15,  8,  6}, 
61             { 1,  4, 11, 13, 12,  3,  7, 14, 10, 15,  6,  8,  0,  5,  9,  2}, 
62             { 6, 11, 13,  8,  1,  4, 10,  7,  9,  5,  0, 15, 14,  2,  3, 12}
63         }, 
64         //S8
65         {
66             {13,  2,  8,  4,  6, 15, 11,  1, 10,  9,  3, 14,  5,  0, 12,  7}, 
67             { 1, 15, 13,  8, 10,  3,  7,  4, 12,  5,  6, 11,  0, 14,  9,  2}, 
68             { 7, 11,  4,  1,  9, 12, 14,  2,  0,  6, 10, 13, 15,  3,  5,  8}, 
69             { 2,  1, 14,  7,  4, 10,  8, 13, 15, 12,  9,  0,  3,  5,  6, 11}
70         }
71 };
72 
73 //置換運算矩陣
74 static int[] P = {
75         16,  7, 20, 21, 
76         29, 12, 28, 17, 
77          1, 15, 23, 26, 
78          5, 18, 31, 10, 
79          2,  8, 24, 14, 
80         32, 27,  3,  9, 
81         19, 13, 30,  6, 
82         22, 11,  4, 25
83 };
 1 /**
 2  * 輪函數
 3  * @param A  32位輸入
 4  * @param K  48位子密鑰
 5  * @return   32位輸出
 6  */
 7 static byte[] f(byte[] A, byte[] K) {
 8     byte[] t = new byte[48];
 9     byte[] r = new byte[32];
10     byte[] result = new byte[32];
11     //選擇運算E
12     for (int i = 0; i < 48; i++) 
13         t[i] = A[E[i] - 1];
14     //模2相加
15     for (int i = 0; i < 48; i++) 
16         t[i] = (byte) (t[i] ^ K[i]);
17     //代替函數組S
18     for (int i = 0, a = 0; i < 48; i += 6, a += 4) {
19         int j = t[i] * 2 + t[i + 5];   //b1b6
20         int k = t[i + 1] * 8 + t[i + 2] * 4 + t[i + 3] * 2 + t[i + 4];   //b2b3b4b5
21         byte[] b = Integer.toBinaryString(S[i / 6][j][k] + 16).substring(1).getBytes();
22         for (int n = 0; n < 4; n++) 
23             r[a + n] = (byte) (b[n] - '0');
24     }
25     //置換運算P
26     for (int i = 0; i < 32; i++) 
27         result[i] = r[P[i] - 1];
28     return result;
29 }

逆初始置換IP-1

//逆初始置換矩陣
static int[] rIP = {
        40,  8, 48, 16, 56, 24, 64, 32, 
        39,  7, 47, 15, 55, 23, 63, 31, 
        38,  6, 46, 14, 54, 22, 62, 30, 
        37,  5, 45, 13, 53, 21, 61, 29, 
        36,  4, 44, 12, 52, 20, 60, 28, 
        35,  3, 43, 11, 51, 19, 59, 27, 
        34,  2, 42, 10, 50, 18, 58, 26, 
        33,  1, 41,  9, 49, 17, 57, 25
};
 1 /**
 2  * 逆初始置換IP^-1
 3  * @param text  64位數據
 4  * @return
 5  */
 6 static byte[] rIP(byte[] text) {
 7     byte[] newtext = new byte[64];
 8     for (int i = 0; i < 64; i++) 
 9         newtext[i] = text[rIP[i] - 1];
10     return newtext;
11 }

 加解密過程

 1 /**
 2  * 加密
 3  * @param plaintext  64位明文
 4  * @param sKey       64位密鑰
 5  * @return           64位密文
 6  */
 7 static byte[] encrypt(byte[] plaintext, byte[] sKey) {
 8     byte[][] L = new byte[17][32];
 9     byte[][] R = new byte[17][32];
10     byte[] ciphertext = new byte[64];
11     //子密鑰的產生
12     byte[][] K = DESUtil.generateKeys(sKey);
13     //初始置換IP
14     plaintext = DESUtil.IP(plaintext);
15     //將明文分成左半部分L0和右半部分R0
16     for (int i = 0; i < 32; i++) {
17         L[0][i] = plaintext[i];
18         R[0][i] = plaintext[i + 32];
19     }
20     //加密迭代
21     for (int i = 1; i <= 16; i++) {
22         L[i] = R[i - 1];
23         R[i] = xor(L[i - 1], DESUtil.f(R[i - 1], K[i - 1]));
24     }
25     //以R16為左半部分，L16為右半部分合併
26     for (int i = 0; i < 32; i++) {
27         ciphertext[i] = R[16][i];
28         ciphertext[i + 32] = L[16][i];
29     }
30     //逆初始置換IP^-1
31     ciphertext = DESUtil.rIP(ciphertext);
32     return ciphertext;
33 }
 1 /**
 2  * 解密
 3  * @param ciphertext  64位密文
 4  * @param sKey        64位密鑰
 5  * @return            64位明文
 6  */
 7 static byte[] decrypt(byte[] ciphertext, byte[] sKey) {
 8     byte[][] L = new byte[17][32];
 9     byte[][] R = new byte[17][32];
10     byte[] plaintext = new byte[64];
11     //子密鑰的產生
12     byte[][] K = DESUtil.generateKeys(sKey);
13     //初始置換IP
14     ciphertext = DESUtil.IP(ciphertext);
15     //將密文分成左半部分R16和右半部分L16
16     for (int i = 0; i < 32; i++) {
17         R[16][i] = ciphertext[i];
18         L[16][i] = ciphertext[i + 32];
19     }
20     //解密迭代
21     for (int i = 16; i >= 1; i--) {
22         L[i - 1] = xor(R[i], DESUtil.f(L[i], K[i - 1]));
23         R[i - 1] = L[i];
24         R[i] = xor(L[i - 1], DESUtil.f(R[i - 1], K[i - 1]));
25     }
26     //以L0為左半部分，R0為右半部分合併
27     for (int i = 0; i < 32; i++) {
28         plaintext[i] = L[0][i];
29         plaintext[i + 32] = R[0][i];
30     }
31     //逆初始置換IP^-1
32     plaintext = DESUtil.rIP(plaintext);
33     return plaintext;
34 }
 1 /**
 2  * 兩數組異或
 3  * @param a
 4  * @param b
 5  * @return
 6  */
 7 static byte[] xor(byte[] a, byte[] b) {
 8     byte[] c = new byte[a.length];
 9     for (int i = 0; i < a.length; i++) 
10         c[i] = (byte) (a[i] ^ b[i]);
11     return c;
12 }

測試

測試數據

　　密鑰：00110001 00110010 00110011 00110100 00110101 00110110 00110111 00111000

　　明文：00110000 00110001 00110010 00110011 00110100 00110101 00110110 00110111

運行結果

　　

參考文獻

　　張煥國，唐明.密碼學引論（第三版）.武漢大學出版社，2015年


您的分享是我們最大的動力!

-Advertisement-
Play Games
更多相關文章
  • JavaBean到JSon格式的轉換例子的代碼
    內容過程，把做工程過程較好的內容片段備份一次，如下的內容是關於 JavaBean到JSon格式的轉換例子的內容，應該對各朋友有一些用處。 User u = new User(); u.setId(1); u.setName("lizhi"); u.setAge(24); u.setHeigh("17 ...
  • SpringCloud學習系列之二 ----- 服務消費者(Feign)和負載均衡(Ribbon)
    本篇主要介紹的是SpringCloud中的服務消費者(Feign)和負載均衡(Ribbon)功能的實現以及使用Feign結合Ribbon實現負載均衡。 ...
  • 笨辦法學Python - 習題5: More Variables and Printing
    1、習題 4: 更多的變數和列印 學習目標： 瞭解用戶輸入方法，明白pthon2和Python3之間的用戶輸入的區別。瞭解格式化字元串(format string)的概念，學會如何創建包含變數內容的字元串。使用專門的格式和語法把變數的內容放到字元串里，然後進行格式化的列印輸出。 1.1、用戶輸入 在 ...
  • spring之旅第一篇-初識spring
    一、概述 只要用框架開發java，一定躲不過spring，Spring是一個輕量級的Java開源框架，存在的目的是用於構建輕量級的J2EE應用。Spring的核心是控制反轉(IOC)和麵向切麵編程(AOP)。spring有如下特點： 輕量級：應用大小和應用開支，包括應用方式 DI/IoC：提供松耦合 ...
  • Spring Security（三）
    Spring Security（三） 個性化用戶認證流程 自定義登錄頁面 在配置類中指定登錄頁面和接收登錄的 url 在項目中新建登錄頁面 啟動項目時再訪問 Security 就會跳轉到你自已定義的登陸頁面讓你登錄。 深入定義（判斷是PC端還是移動端，PC端跳轉頁面，移動端響應 json） 創建一個 ...
  • Eclipse C/C++開發環境搭建
    今天在家裡的Linux系統上，試著搭建Eclipse C/C++開發環境，最後終獲成功。下麵貼上兩篇對搭建過程很有幫助的文章 用 Eclipse 平臺進行 C/C++ 開發 https://www.ibm.com/developerworks/cn/linux/opensource/os-ecc/ ...
  • Python學習筆記：PEP8常用編程規範
    PEP8編碼規範是一種非常優秀的編碼規範，也得到了Python程式員的普遍認可，如果實踐中或者項目中沒有統一的編碼規範，建議儘量遵循PEP8編碼規範，當然如果項目中已經有了自身的編碼規範，應當優先遵循自身的編碼規範，哪怕原先的代碼風格在你看來很糟糕，也要儘量與源代碼風格保持一致。原文地址：https ...
  • Spring讀取配置文件 @Value
    最近在學習Spring如何讀取配置文件，記錄下方便自己也方便別人； 大致分為兩類吧，一種的思路是利用Spring的beanFactoryPostProcessor讀取配置文件內容到記憶體中，也就是應用程式的某個對象的屬性中，然後設置上去； 另外一種思路就是SPEL表達式，這是Spring3.x的特性， ...
一周排行
    -Advertisement-
    Play Games
  • 移動開發（一）：使用.NET MAUI開發第一個安卓APP
    移動開發（一）：使用.NET MAUI開發第一個安卓APP 對於工作多年的C#程式員來說，近來想嘗試開發一款安卓APP，考慮了很久最終選擇使用.NET MAUI這個微軟官方的框架來嘗試體驗開發安卓APP，畢竟是使用Visual Studio開發工具，使用起來也比較的順手，結合微軟官方的教程進行了安卓 ...
  • wpf ToggleButton選中效果和一個登錄界面
    前言 QuestPDF 是一個開源 .NET 庫，用於生成 PDF 文檔。使用了C# Fluent API方式可簡化開發、減少錯誤並提高工作效率。利用它可以輕鬆生成 PDF 報告、發票、導出文件等。 項目介紹 QuestPDF 是一個革命性的開源 .NET 庫，它徹底改變了我們生成 PDF 文檔的方 ...
  • 彈幕樹洞項目功能新增篇
    項目地址 項目後端地址： https://github.com/ZyPLJ/ZYTteeHole 項目前端頁面地址： ZyPLJ/TreeHoleVue (github.com) https://github.com/ZyPLJ/TreeHoleVue 目前項目測試訪問地址： http://tree ...
  • 第27篇 sqlserver2022詳細安裝步驟
    話不多說，直接開乾 一.下載 1.官方鏈接下載： https://www.microsoft.com/zh-cn/sql-server/sql-server-downloads 2.在下載目錄中找到下麵這個小的安裝包 SQL2022-SSEI-Dev.exe，運行開始下載SQL server； 二. ...
  • .NET 開源高性能 MQTT 類庫
    前言 隨著物聯網（IoT）技術的迅猛發展，MQTT（消息隊列遙測傳輸）協議憑藉其輕量級和高效性，已成為眾多物聯網應用的首選通信標準。 MQTTnet 作為一個高性能的 .NET 開源庫，為 .NET 平臺上的 MQTT 客戶端與伺服器開發提供了強大的支持。 本文將全面介紹 MQTTnet 的核心功能 ...
  • Serilog文檔翻譯系列（六） - 可用的接收器、增強器、格式化輸出
    Serilog支持多種接收器用於日誌存儲，增強器用於添加屬性，LogContext管理動態屬性，支持多種輸出格式包括純文本、JSON及ExpressionTemplate。還提供了自定義格式化選項，適用於不同需求。 ...
  • 警惕 Visual Studio 屬性求值副作用導致邏輯不符合預期
    目錄簡介獲取 HTML 文檔解析 HTML 文檔測試參考文章 簡介 動態內容網站使用 JavaScript 腳本動態檢索和渲染數據，爬取信息時需要模擬瀏覽器行為，否則獲取到的源碼基本是空的。 本文使用的爬取步驟如下： 使用 Selenium 獲取渲染後的 HTML 文檔 使用 HtmlAgility ...
  • [使用目前最新版]HybridCLR6.9.0+YooAsset2.2.4實現純C# Unity熱更新方案 (一)
    1.前言 什麼是熱更新 游戲或者軟體更新時，無需重新下載客戶端進行安裝，而是在應用程式啟動的情況下，在內部進行資源或者代碼更新 Unity目前常用熱更新解決方案 HybridCLR，Xlua，ILRuntime等 Unity目前常用資源管理解決方案 AssetBundles，Addressable， ...
  • 在 ASP.NET Core Web API 中使用操作篩選器統一處理通用操作
    本文章主要是在C# ASP.NET Core Web API框架實現向手機發送驗證碼簡訊功能。這裡我選擇是一個互億無線簡訊驗證碼平臺，其實像阿裡雲，騰訊雲上面也可以。 首先我們先去 互億無線 https://www.ihuyi.com/api/sms.html 去註冊一個賬號 註冊完成賬號後，它會送 ...
  • 第28篇 如何.net中實現高效可靠數據同步api
    通過以下方式可以高效，並保證數據同步的可靠性 1.API設計 使用RESTful設計，確保API端點明確，並使用適當的HTTP方法（如POST用於創建，PUT用於更新）。 設計清晰的請求和響應模型，以確保客戶端能夠理解預期格式。 2.數據驗證 在伺服器端進行嚴格的數據驗證，確保接收到的數據符合預期格 ...
所有分類