通過上篇文章,大家已經能夠清楚的瞭解到treeMap插入結點的過程,那麼本篇文章就來分析下TreeMap刪除一個結點時,內部數據結構發生了怎樣的變化。 TreeMap刪除某個結點的源碼分析 1 /** 2 * 刪除節點,並平衡紅黑樹的操作 3 * 4 * @Param Entry<K,V> p 要刪 ...
通過上篇文章,大家已經能夠清楚的瞭解到treeMap插入結點的過程,那麼本篇文章就來分析下TreeMap刪除一個結點時,內部數據結構發生了怎樣的變化。
TreeMap刪除某個結點的源碼分析

1 /** 2 * 刪除節點,並平衡紅黑樹的操作 3 * 4 * @Param Entry<K,V> p 要刪除的節點Entry 5 */ 6 private void deleteEntry(Entry<K,V> p) { 7 modCount++; 8 size--; //節點總數-1 9 10 if (p.left != null && p.right != null) { //當前要刪除的節點左右子節點都不為空 11 Entry<K,V> s = successor(p); //找到一個待刪除節點的繼承者節點s 12 //將指向s節點,後續所有對p的節點判斷其實都是對s節點判斷 13 p.key = s.key; 14 p.value = s.value; 15 p = s; 16 } 17 18 //替代節點選擇為當前被刪除節點的左子節點(優先)或右子節點 19 Entry<K,V> replacement = (p.left != null ? p.left : p.right); 20 21 if (replacement != null) { //替代節點(被刪除節點的子節點)不為空 22 23 replacement.parent = p.parent; //將替代節點的父節點指向被刪除節點的父節點 24 if (p.parent == null) //如果被刪除節點的父節點為null (即被刪除的節點就是樹的根節點,且根節點下麵還有其他節點) 25 root = replacement; //將根節點設置為替換節點 26 else if (p == p.parent.left) //如果原先被刪除節點是左子樹 插入 27 p.parent.left = replacement; //則將替換節點也保持左子樹插入(將替換節點與被刪除節點的父節點左子節點建立引用) 28 else //如果原先被刪除節點是右子樹 插入 29 p.parent.right = replacement; //則將替換節點也保持右子樹插入(將替換節點與被刪除節點的父節點右子節點建立引用) 30 31 //將被刪除節點的左子節點、右子節點、父節點引用全部置為null 32 p.left = p.right = p.parent = null; 33 34 //刪除後要執行後續的保證紅黑樹規則的操作 35 if (p.color == BLACK) //如果被刪除節點是黑色的 36 fixAfterDeletion(replacement); //調用刪除後修正紅黑樹規則的方法 37 } else if (p.parent == null) { //被刪除節點就是根節點,且整個樹中就只有一個根節點的情況 38 root = null; //將根節點置為null(此時整個樹中就沒有節點了) 39 } else { //被刪除節點沒有子節點可替代的情況 (被刪除節點是葉子節點) 40 if (p.color == BLACK) //如果被刪除節點是黑色的 41 fixAfterDeletion(p); //調用刪除後修正紅黑樹規則的方法 42 43 if (p.parent != null) { //如果被刪除節點的父節點不為null 44 if (p == p.parent.left) //如果原先被刪除節點是左子樹 插入 45 p.parent.left = null; //刪除節點後將被刪除節點的父節點的左子節點置為null 46 else if (p == p.parent.right) //如果原先被刪除節點是右子樹 插入 47 p.parent.right = null; //刪除節點後將被刪除節點的父節點的右子節點置為null 48 p.parent = null; //將被刪除節點的父節點引用置為null(即將被刪除節點從樹中移除) 49 } 50 } 51 }View Code
源碼邏輯很簡單,主要就是分為刪除結點有子結點和無子結點,而無子結點又分為刪除的是根結點或葉子結點這三種情況
然後如果被刪除結點是黑色的,那麼要註意下可能繼承者和被刪除結點的父結點都是紅色的情況,此時需要做平衡紅黑樹的操作。
這裡需要註意的方法有兩個: 第11行的 successor() 方法 以及 第36行的 fixAfterDeletion() 方法。
分別貼一下這兩個方法的源碼:
1 /** 2 * 返回被刪除節點的繼承者節點 3 */ 4 static <K,V> TreeMap.Entry<K,V> successor(Entry<K,V> t) { 5 if (t == null) //如果被刪除節點為空,則直接返回null 6 return null; 7 else if (t.right != null) { //如果被刪除節點的右子節點不為空 8 Entry<K,V> p = t.right; //將被刪除節點的右子節點記錄下來 9 while (p.left != null) //從該節點開始迴圈向下查找左子節點,直至找到葉子節點後返回該葉子節點 10 p = p.left; 11 return p; 12 } else { //如果被刪除節點的右子節點為空 13 Entry<K,V> p = t.parent; //將被刪除節點的父節點用p變數記錄 14 Entry<K,V> ch = t; //被刪除節點用ch變數記錄 15 while (p != null && ch == p.right) {//從被刪除節點開始迴圈向上查找父節點,直到父節點為空或者父節點沒有右子節點,返回該父節點 16 ch = p; 17 p = p.parent; 18 } 19 return p; 20 } 21 }

1 /** 2 * 樹刪除一個節點後,將其根據紅黑樹的規則進行修正 3 * @param x 當前刪除的節點 4 */ 5 private void fixAfterDeletion(Entry<K,V> x) { 6 //迴圈遍歷,x剛開始為被刪除的節點 7 while (x != root && colorOf(x) == BLACK) { //如果當前遍歷到的節點不是根節點且為黑色 8 if (x == leftOf(parentOf(x))) { //如果當前遍歷到的節點是其父節點的左子節點 9 Entry<K,V> sib = rightOf(parentOf(x)); //將當前遍歷到的節點的父節點的右子節點用sib變數保存(即和當前節點平級的另一個節點) 10 11 if (colorOf(sib) == RED) { //如果sib引用的節點是紅色的 12 setColor(sib, BLACK); //將sib引用的節點設置為黑色 13 setColor(parentOf(x), RED); //將當前遍歷到節點的父節點設置為紅色 14 rotateLeft(parentOf(x)); //對當前遍歷到節點的父節點進行一次左旋操作 15 sib = rightOf(parentOf(x)); //sib引用的節點變更為旋轉後被刪除節點的父節點的右子節點 16 } 17 18 if (colorOf(leftOf(sib)) == BLACK && 19 colorOf(rightOf(sib)) == BLACK) { //如果sib引用節點的左、右子節點都是黑色的 20 setColor(sib, RED); //將sib引用的節點設置為紅色 21 x = parentOf(x); //下一次遍歷的節點變更為當前遍歷到節點的父節點 22 } else { //如果sib引用節點的左、右子節點不全是黑色的 23 if (colorOf(rightOf(sib)) == BLACK) { //如果sib引用節點的右子節點是黑色的 24 setColor(leftOf(sib), BLACK); //將sib引用節點的左子節點設置為黑色 25 setColor(sib, RED); //sib引用節點設置為紅色 26 rotateRight(sib); //對sib節點進行一次右旋操作 27 sib = rightOf(parentOf(x)); //sib引用的節點變更為當前遍歷到的節點的父節點的右子節點 28 } 29 setColor(sib, colorOf(parentOf(x))); //將sib引用節點的顏色設置為 當前遍歷到節點的父節點 一樣的顏色 30 setColor(parentOf(x), BLACK); //將當前遍歷到節點的父節點設置為黑色 31 setColor(rightOf(sib), BLACK); //將sib引用節點的右子節點設置為黑色 32 rotateLeft(parentOf(x)); //對當前遍歷到的節點的父節點進行一次左旋操作 33 x = root; //下一次遍歷的節點變更為根節點 34 } 35 } else { // 當前遍歷到的節點是其父節點的右子節點,和上述情況相似,不再贅述 36 Entry<K,V> sib = leftOf(parentOf(x)); 37 38 if (colorOf(sib) == RED) { 39 setColor(sib, BLACK); 40 setColor(parentOf(x), RED); 41 rotateRight(parentOf(x)); 42 sib = leftOf(parentOf(x)); 43 } 44 45 if (colorOf(rightOf(sib)) == BLACK && 46 colorOf(leftOf(sib)) == BLACK) { 47 setColor(sib, RED); 48 x = parentOf(x); 49 } else { 50 if (colorOf(leftOf(sib)) == BLACK) { 51 setColor(rightOf(sib), BLACK); 52 setColor(sib, RED); 53 rotateLeft(sib); 54 sib = leftOf(parentOf(x)); 55 } 56 setColor(sib, colorOf(parentOf(x))); 57 setColor(parentOf(x), BLACK); 58 setColor(leftOf(sib), BLACK); 59 rotateRight(parentOf(x)); 60 x = root; 61 } 62 } 63 } 64 65 setColor(x, BLACK); 66 }View Code
可能光看這兩個方法的源碼不太好理解,下麵就以刪除幾個結點的實例,一步一步跟蹤下源碼看看數據結構到底發生了哪些變化。
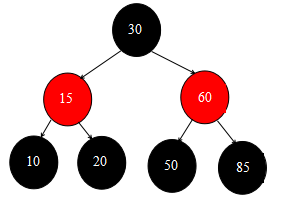
先回顧下上一篇文章插入結點完成後的紅黑樹狀態圖:
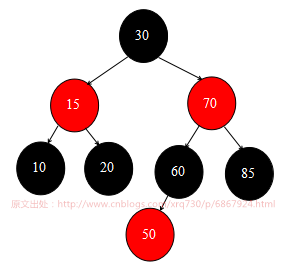
好,那麼首先來刪除根結點30。因為30結點既有左子結點,又有右子結點,所以在deleteEntry()方法中需要調用successor() 方法尋找繼承者結點。
查看successor() 方法源碼,可以發現會走第7行的 else if 邏輯,然後從70結點開始迴圈查找左子結點,直到找到葉子結點50為止,所以最終的繼承者結點就是50,下麵的三行代碼會將根結點30的key-value變為繼承者的key-value,所以現在根結點為50,黑色。
然後下一行會取得replacement變數,因為現在p=s了,即這裡的p.left實際判斷的是葉子結點50是否有左子結點,很顯然葉子結點50既沒有左子結點也沒有右子結點,所以最後replacement = null。
而葉子結點50是有父結點的,所以不會走 else if (p.parent == null) 分支,而是走下麵的else{}分支。葉子結點50目前是紅色的,所以不需要做平衡紅黑樹的操作。
再往下,很顯然葉子結點50是有父結點的,所以會走 if (p.parent != null) 的分支,而這個分支裡面又是一個if-else分支,這裡判斷的是當前結點是左子樹插入還是右子樹插入,葉子結點50很明顯是左子樹插入,所以會執行 p.parent.left = null 這行代碼,即把葉子結點50給刪除掉了。
全部過程執行完後,紅黑樹當前的狀態圖如下所示:
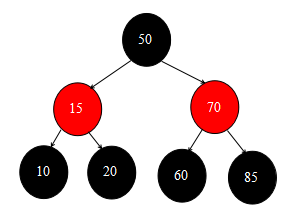
經過一次刪除操作後,童鞋們是否對這兩個方法有點印象了呢?不過這次刪除30結點我們找到的繼承者結點50是紅色的,所以沒有走修正紅黑樹平衡的操作。那麼下麵就再刪除一個結點,讓它進行平衡紅黑樹的操作。
還是以最原始的紅黑樹狀態圖為基準,這次我們來刪除結點70。70也需要尋找繼承者結點,因為70有右子結點,所以會走 else if (t.right != null) 這個分支邏輯,然後指針移動到85結點,而又因為85沒有左子結點,所以不符合下麵的 while (p.left != null)迴圈條件,方法結束,最後選擇的繼承者結點就是85結點。
然後和上面一樣,會走三行代碼,將70結點變更為85結點,然後將指針指向85結點。很顯然85結點既沒有左子結點也沒有右子結點,所以replacement = null。然後85結點是有父結點的,所以和上面一樣走的是else{}分支。
註意,這裡和上面的不同之處在於,目前指針是指向85這個節點的,而這個節點是黑色的,所以在else{}分支里的 if (p.color == BLACK) 為true,則會調用 fixAfterDeletion(p) 這個方法進行紅黑樹的修正操作。
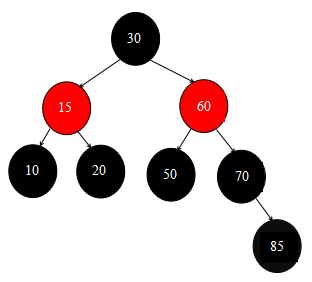
在調用修正操作之前,紅黑樹的狀態是這樣的:
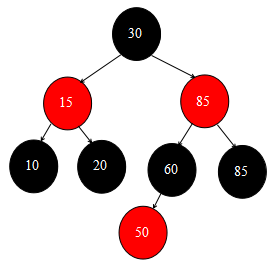
好,接下來我們看一下具體的修正操作幹了哪些事情。
首先此時指針指向的黑色85結點是滿足 while (x != root && colorOf(x) == BLACK) 這個迴圈條件的,然後這個節點是右子樹插入的,所以會走else{}分支。
然後下一步的sib節點取得是父結點的左子結點,即60結點,而60結點是黑色,所以不會走 if (colorOf(sib) == RED) 這個分支邏輯。
然而60結點的左右子結點都不是黑色的,所以會走下麵的else{}分支,並且不會走 else分支中的 if (colorOf(leftOf(sib)) == BLACK) 這個判斷,只會從第 56 行的代碼開始走
setColor(sib, colorOf(parentOf(x))) 是將60結點的顏色設置為何黑色85結點的父結點(即紅色85結點)的顏色,所以此時60結點變為紅色。
setColor(parentOf(x), BLACK) 這一行又把紅色的85結點設置為了黑色
setColor(leftOf(sib), BLACK) 這一行又將50結點設置成了黑色,此時除了60結點為紅色,其餘的50、85、85結點都是黑色
rotateRight(parentOf(x)) 這一行以之前為紅色的85結點為中心,做一次右旋操作。忘記旋轉操作的童鞋看看前面的帖子,就不難理解啦。
然後將指針移動回根結點,並設置根結點為黑色,此時整個修正紅黑樹操作就結束了。此時紅黑樹狀態圖如下所示:
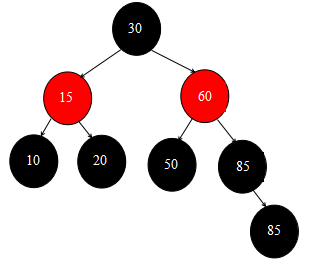
註意:不要忘記再回到之前的deleteEntry方法中去,只是走完了修正紅黑樹的方法,但整個刪除操作還沒全部結束呢!
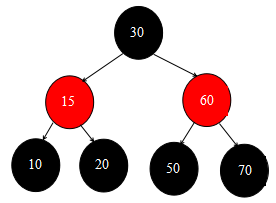
回到原方法的 if (p.parent != null)分支,此時85結點是有父結點的,所以會走這個分支邏輯,然後85又是右子樹插入的,所以會走 else if (p == p.parent.right) 這個分支邏輯
然後這行 p.parent.right = null 會將葉子結點85刪除,此時才是真正走完了整個刪除節點的操作。此時童鞋們小本本上的紅黑樹應該是這樣的喲:
好了,大家是不是覺得其實紅黑樹的操作並不是很困難呢?只要肯踏踏實實、一步一步的去仔細分析每一步紅黑樹是如何變化的就能夠輕鬆得到結果。
最後還有一個刪除葉子結點的沒有講,比較簡單就讓童鞋們自己去研究實踐吧!
在這裡放上兩張狀態圖,以便童鞋們進行驗證(圖中的狀態是以刪除葉子結點85為例所得到的結果):
1.進行紅黑樹修正操作之後的狀態圖:
2.刪除葉子結點85操作全部結束後的狀態圖:
註:以上圖片出處均為 博客園——五月的倉頡,非本人原創!
到這裡,關於紅黑樹的所有知識全部都講解完畢,並且集合的基礎知識也暫告一段落了。
有的童鞋會問,怎麼只講了List、Map介面下的一些常用工具類,Set介面的怎麼不講了呢?
大家可以去看下HashSet、TreeSet的源碼相關實現,其實就是HashSet、TreeSet去掉了Value而已,絕大多數實現都是一樣的,所以我這裡就不再去細說了
註意我在這個集合分類中所講的集合類都是非線程安全的,像CopyOnWriteArrayList、ConcurrentHashMap、BlockingQueue等線程安全的集合工具類我會放在多線程的分類主題中去講解。
OK,接下來我會更新一些多線程相關的知識,下期見!




