上學期學了一些matlab的知識,這學期再用時竟然發現已經忘得差不多了(┬_┬) 於是決定重新開始並將它們記錄下來,也方便自己以後查漏補缺! M文件編程 腳本文件 matlab有自己的命令行視窗,對於簡單的命令,可以直接在命令行視窗輸入,但隨著命令行的增加或者命令本身複雜度的增加,再使用命令行就顯得 ...
上學期學了一些matlab的知識,這學期再用時竟然發現已經忘得差不多了(┬_┬)
於是決定重新開始並將它們記錄下來,也方便自己以後查漏補缺!
M文件編程
- 腳本文件
matlab有自己的命令行視窗,對於簡單的命令,可以直接在命令行視窗輸入,但隨著命令行的增加或者命令本身複雜度的增加,再使用命令行就顯得有些不便了,這時就需要腳本文件了。可以說,腳本文件是matlab指令集合的封裝。
- 函數文件
函數文件以function開始,end結束,這也是區別於腳本文件的地方。
在function後面接著定義輸出參數,函數名和輸入參數,比如:
function [x,y,z] = math_count(a,b,c)
x,y,z是輸出參數,以方框括起來,math_count是函數名,a,b,c是輸入參數,以圓括弧括起來。
也可以沒有參數,比如:
function printresults(x,y)
printresults是函數名,x和y是輸入參數,沒有輸出參數。
- 數據類型
matlab共有6中基本數據類型,分別是數值類型、邏輯類型、字元串、函數句柄、結構體和單元數組。這裡我們簡單地介紹前四種。
- 數值類型
基本的數值類型包括整數類型和浮點數類型,額外的數值類型還有複數類型、無窮量(Inf)和非數值量(NaN),後面的兩種算是matlab的特色類型,當然要記錄一下啦!
- 複數類型
複數包括實部和虛部兩部分,matlab中預設使用i和j作為複數的虛部標誌。創建複數時,可以直接利用複數形式進行輸入或使用函數complex。
z=1+2i %利用複數形式進行輸入
輸出結果:
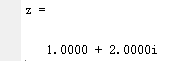
z=complex(2,3) %利用complex(x,y)函數進行輸入
輸出結果:
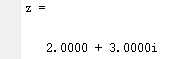
z=complex(2)%利用complex(x),如果x是實數,z=x+0i,如果x是複數,z=x
輸出結果:
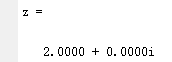
-
- 無窮量(Inf)和非數值量(NaN)
Matlab中使用Inf和-Inf分別代表正無窮量和負無窮量,NaN代表非數值量。
正負無窮量通常由於運算溢出而產生的結果,而非數值量是由於0/0或Inf/Inf非正常運算產生的結果,並且這兩個NaN是不同的。
Inf和NaN是Matlab中的特殊變數,除此之外,Matlab還有一些特殊的變數
- ans:系統預設的用作保存運算結果的變數名
- pi:圓周率
- eps:機器零閥值,Matlab中的最小數
2.邏輯類型
Matlab把任何非0值當作為真,輸出為1,把零當作假,輸出為0.
邏輯類型數據進行運算時需要用到關係操作符和邏輯運算符。
對於Matlab的關係操作符,與c/c++基本相同,只有不等號有所不同,在c/c++中不等號為!=,而Matlab中不等號是~ =。
Matlab中的邏輯操作符如下表所示:
| 邏輯運算符 | 說明 |
|---|---|
| & | 與 |
| | | 或 |
| ~ | 非 |
3.字元和字元串
字元和字元串分別是字元數組和字元串數組中的文本。
- 字元數組是一個字元序列,如c='Hello Word!'
- 字元串數組是文本片段的容器,字元串數組提供一組用於將文本處理為數據的函數。從R2017a開始,字元串也可以使用雙引號創建,如str="You are best!"
- string函數
R2016b以後,可以使用字元串數組string代替字元數組。官方文檔表明,還可以按照標準數組運算對字元串數組
進行索引、重構和串聯,還可以使用 + 運算符向字元串追加文本。(一切都在向c++看齊啊)
4.函數句柄
函數句柄是一種間接調用函數的方式,相當於對一個函數取別名。
例如:如果你有一個函數為myfunction,現在給定語句
f=@myfunction %f是一個句柄,可以通過f調用myfunction
可以通過函數句柄構造匿名函數或指定回調函數,也可以函數句柄將一個函數傳遞給另一個函數,或者從主函數內部調用局部函數
下麵給出通過函數句柄間接調用函數的例子:
在命令行視窗輸入:
Handle=@sin; %也可以自己建立函數,通過函數句柄間接調用
>> x=0:pi/4:pi; %通過冒號創建一維數組,0是第一個數,每次以pi/4為單位遞增,pi是最後一個數
>> y=Handle(x)
輸出結果:
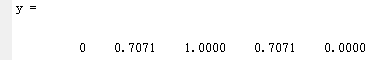
有同學可能會問,直接調用不也是可以嗎,的確可以,但函數句柄有更多的優點,列舉幾個
- 提高運行速度。matlab對函數的調用每次都要搜索所有的路徑,使用函數句柄可以減少搜索,提高運行速度。
- 使用更方便。比如說,我在這個目錄運行後,創建了本目錄的一個函數句柄,當我轉到其他的目錄下的時候,創建的函數句柄還是可以直接調用的,而不需要把那個函數文件拷貝 過來。因為你創建的函數句柄中已經包含了路徑。
- 控制流
Matlab的控制流也與c/c++大體相同,唯一要註意的是每個條件都有相應的end關鍵字。
- 順序結構
- 選擇結構
- if—end
- if—else—end
- if—elseif—else—end
示例:
新建腳本文件,保存為exe1_1
x=input('enter''x'':');%input函數返回你輸入的整數,提示信息用''括起來,如果想要輸出單引號,兩個單引號'' ''即可
if(x>0)
y=1;
elseif(x==0)
y=0;
else y=-1;
end %不要忘記加end,Matlab不會自動補全end,最好一開始就寫下來,養成良好的編程習慣至關重要
disp(y) %disp作為輸出函數
在命令行視窗調用exe1_1,輸入-5
得到結果:

- switch—case結構
示例:新建腳本文件,保存為ex1_2
1 month=3; 2 switch month 3 case {3,4,5} 4 season='spring' %註意Matlab與c/c++語言的switch-case結構不一樣:只要條件滿足,立即返回,不對後面的語句做判斷,這也是為什麼不用加break的原因。 5 case {6,7,8} 6 season='summer' 7 case {9,10,11} 8 season='autumn' 9 otherwise 10 season='winter' 11 end
得到結果:
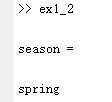
註意
1.M文件的搜索路徑必須與當前路徑一致,否則運行會出錯,搜索路徑即保存M文件的位置。可以直接修改當前路徑與搜索路徑一致,也可以添加搜索路徑,這樣就一勞永逸了。

2.如果遇到不認識的函數,可以利用help/doc命令在命令行查找,格式為help/doc function,function為函數名,養成查閱文檔的習慣很重要!
- 迴圈結構
- while,for語句
- break、continue、return ——行尾可以不用加分號
每一個關鍵字後面都要有與之對應的end關鍵字
範例:
使用0.618法(黃金分割法)極小化f(t)=exp(-t)+exp(t),區間為[-1,1]。(即逼近函數在已知區間的極小值,找到對應的t)
0.618法主要思想:
0.618法在給定區間[a,b]內適當插入兩點a1,a2,並計算其函數值。
a1,a2將區間分成三段,通過函數值大小的比較,刪去其中一段,使搜索區間得以縮小,
然後再在保留下來的區間上作同樣的處理,如此迭代下去,從而得到極小點的數值近似解。
0.618法主要步驟:
1.在區間[a,b]內分別按照0.618和0.382的比例處取點a1 ,a2, 把[a,b]分為三段。
2.如果f(a1)>f(a2),令a=a1,a1=a2,a2=a+0.618*(b-a)
3.如果f(a1)<f(a2) ,令b=a2,a2=a1,a1=a+0.382*(b-a)
4.如果滿足迭代條件或者超出給定迭代次數,程式終止,否則繼續運行下去。
新建名為fai.m的函數和zero_soe.m的函數
1 function z= fai(t)
2 % fai函數
3 % 給定函數
4 z=1*exp(-t)+1*exp(t);
5 end
1 function [k] = zero_soe(a0,b0,iter,tol)
2 %UNTITLED3 精確線性搜索之0.618法
3 % a0,b0分別代表左端點,右端點
4 % iter代表給定的迭代次數
5 % tol代表誤差限
6 m=a0+0.382*(b0-a0); %試探點lameda0
7 n=a0+0.618*(b0-a0); %試探點u0
8 ym=fai(m);
9 yn=fai(n);
10 count=0; %現有的迭代次數
11 while(count<iter)
12 if(ym>yn)
13 if(b0-m<=tol)
14 k=n;
15 return;
16 else
17 a0=m;
18 m=n;
19 ym=yn;
20 n=a0+0.618*(b0-a0);
21 yn=fai(n);
22 count=count+1;
23 end
24 else
25 if(n-a0<=tol)
26 k=m;
27 return;
28 else
29 b0=n;
30 n=m;
31 yn=ym;
32 m=a0+0.382*(b0-a0);
33 ym=fai(m);
34 count=count+1;
35 end
36 end
37 end
38 if(count>=iter)
39 disp('迭代次數超過給定次數!') ;
40 end
41 end
得到結果:

通過求導可知函數的極小值對應的t等於0,可知極小化的結果是正確的。
(皆大歡喜[]~( ̄▽ ̄)~*)
常用的函數命令
- 輸入命令
- clc:清除命令行視窗
- clf :即clear figure,清楚圖形視窗
- clear:清除工作區的變數,clear all是清除全部變數
- format:設置命令行視窗顯示格式
- iskeyword:確認輸入是否為關鍵字,如果沒有輸入,則輸出全部的關鍵字
- who:顯示當前變數名列表
- whos:顯示變數詳細列表
- which:查看關鍵字的路徑
- 幫助
- help:命令行視窗中函數的幫助
- doc:幫助瀏覽器中的參考頁
- demo:幫助瀏覽器中查看示例
- lookfor:在所有幫助條目中查看關鍵字
常用快捷鍵
- Ctrl+R :註釋(對多行有效)
- Ctrl+T :取消註釋(對多行註釋有效)
- Ctrl+Z :取消上一次操作
- Ctrl+I :自動縮進(對多行有效)
- Ctrl+[ :減少縮進(對多行有效)
- Ctrl+] :增加縮進(對多行有效)
- ↑游標鍵 :選擇最近的一次命令
- Esc:清除當前行
參考資料:
- Matlab 2016a自學一本通 /劉浩,韓晶編著 ~北京:電子工業出版社,2016,12
- Mathworks 中國,附鏈接 Matlab快速入門—Mtahworks中國
還沒有寫完,以後慢慢補吧~


