C#實現AStar尋路演算法_ZenDei技術網路在線

AStar尋路演算法是一種在一個靜態路網中尋找最短路徑的演算法，也是在游戲開發中最常用到的尋路演算法之一；最近剛好需要用到尋路演算法，因此把自己的實現過程記錄下來。先直接上可視化之後的效果圖，圖中黑色方格代表障礙物，綠色的方格代表最終路線，紅色方格為關閉列表，藍色方格為開啟列表；關於這一部分我會在稍後詳細 ...

AStar尋路演算法是一種在一個靜態路網中尋找最短路徑的演算法，也是在游戲開發中最常用到的尋路演算法之一；最近剛好需要用到尋路演算法，因此把自己的實現過程記錄下來。

先直接上可視化之後的效果圖，圖中黑色方格代表障礙物，綠色的方格代表最終路線，紅色方格為關閉列表，藍色方格為開啟列表；關於這一部分我會在稍後詳細敘述。（可視化的實現部分我就不討論了，這一篇主要說一下演算法的實現）

一、演算法原理

在描述具體演算法邏輯之前，需要先理解幾個基本概念：

- 啟髮式搜索：聽起來很炫酷，其實很簡單；想象你在一個九宮格的中間，你現在需要走到九宮格的右上角；這個時候你的第一步有四個選擇：上下左右。雖然你還不知道具體路徑怎麼走，但你知道左邊和下邊距離終點似乎更遠，所以你會優先選擇先往右走或者先往上走。這就是啟髮式搜索——優先搜索最有可能產生最佳路徑的節點；通過啟髮式搜索，可以有效減少不必要的搜索。
- 估價函數：上面說到啟髮式搜索會優先搜索最有可能產生最佳路徑的節點，那麼估價函數的作用就是對節點與終點的距離進行預估。預估距離最短的那個節點，就是目前最有可能產生最佳路徑的節點。
- 開啟列表：當估價函數對一個節點估價完畢後，這個節點就會被放入開啟列表中。那麼開啟列表中的所有節點就是下一步所有可能被搜索的節點。
- 關閉列表：當演算法對開啟列表中最有可能是最佳路徑的節點搜索完畢後，會將這個節點放入關閉列表。那麼關閉列表中的所有節點就是已經搜索完的所有路線的節點。

接下來，我用一個簡單的例子來描述演算法的邏輯。

首先，假設我們有一個4*4的方格，左下角坐標（0，0），右上角坐標（3，3），黑色格子為障礙物；這個時候時候我們需要尋找點（0，1）到點（3，1）的最短路線；這個時候我們把起點加入開啟列表（藍色格子），即所有下一步可能被搜索的節點。

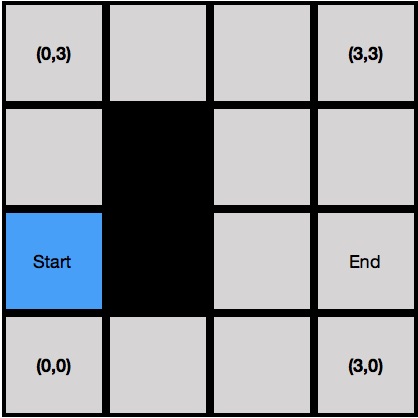
接下來我們要對開啟列表進行搜索了，這個時候開啟列表只有一個格子即起點，因此我們對起點進行搜索：

這個時候我們把起點作為當前節點（即當前正在搜索的節點），然後找出當前節點所有下一步可能的節點，把他們加入開啟列表（藍色格子），表示這些都是下一步可能被搜索的節點。
這個時候我們要對所有新增的節點用估價函數進行估價，估價函數的表達式為f(n)=g(n)+h(n)，其中g(h)代表節點n到起點的實際距離，h(n)即啟發值，代表節點n到終點的預估距離，以節點（0，2）為例子：
- g：可以看到，（0，2）從起點往上移動了一格，假設一個格子邊長為10，那麼當前格子到起點的距離為10，因此g值為10，我們把它標在格子左下角。
- h：h有很多種估價的方式，在這裡我們就直接取忽略障礙物直接走到終點的距離；如圖所示，該節點若要直接走到終點，它的路線為：右-右-右下，那麼它的h值就是：10+10+14 = 34；我們把它標記在格子右下角。
- f：f為包含當前節點的路線的預估總距離，即g+h = 10+34 = 44，我們把它標在格子左上角。
- 父節點：父節點表示當前節點的估價是由哪個節點產生的，或者當前節點是從哪個節點走過來的；因此它的父節點為（0，1），我們用一個箭頭指向（0，1），表示（0，1）是（0，2）的父節點。
對所有下一步可能的節點估價完畢後，我們將當前節點即起點從開啟列表移動到關閉列表中（紅色方格），表示我們對這個節點已經搜索完畢；結果如下圖所示。

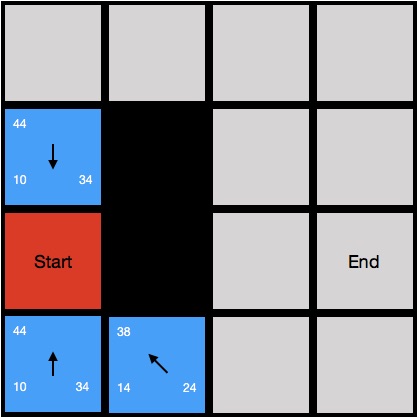
接下來我們繼續對開啟列表進行搜索，經過上一步後，我們的開啟列表有三個節點；這個時候我們尋找f值最小的節點對它進行搜索，可以看到坐標為（1，0）的節點有著最小的f值38；因此節點（1，0）是目前最有可能產生最佳路線的節點，我們把它作為當前節點進行搜索：

這個時候我們重覆上一步的動作，找出當前節點所有下一步可能的節點，並對它們進行估價
在找出節點的過程中，我們發現它左邊的節點是它下一步可能的新節點（0，0）之一，但是左邊的節點已經存在於開啟列表中了；那我們是否讓新節點覆蓋舊節點呢？這個時候我們如果對新產生的節點（0，0）進行估價，我們會發現新產生的節點h值不變，g值為24，f值為24+34 = 58；我們發現新節點的f值58大於舊節點的f值44，那麼我們可以知道新節點所產生的路線總距離大於老節點產生的路線的總距離，因此我們選擇保留老節點。（當然如果我們發現新節點所產生的f值小於老節點所產生的f值，我們就要用新節點覆蓋老節點，因為新節點所產生的路線總距離更近）
估價完畢後，我們對把當前節點從開啟列表移動到關閉列表中（紅色方格），結果如下圖

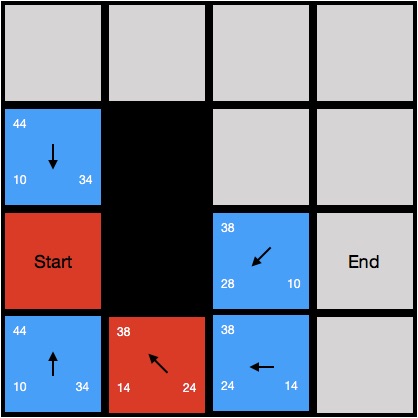
這個時候我們發現最小f值的節點有兩個，我們隨便選一個（2，1）繼續搜索，可以得到下圖的結果：

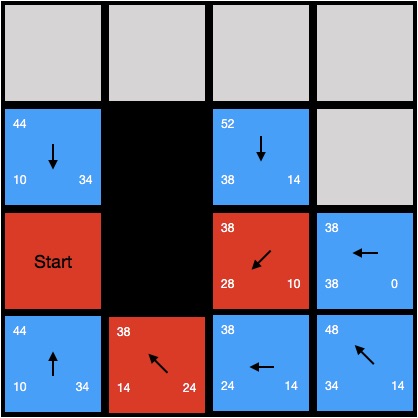
這個時候依然有兩個節點f值最小，我們隨便選一個（3，1），把它作為當前節點，繼續搜索；這個時候我們發現當前節點位置就是終點的位置，我們按照箭頭線路走到起點，於是我們終於找到了路線，如下圖所示：

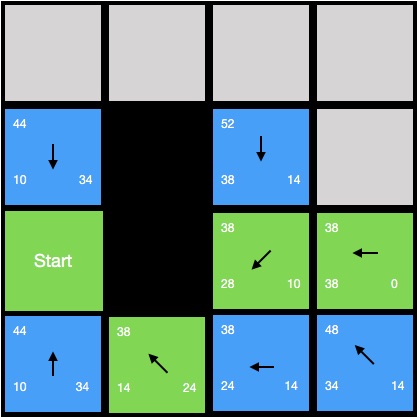
於是我們可以總結一下Astar尋路演算法的演算法邏輯（偽代碼）：

　　new openList；

　　new closeList；

　　openList.Add(start); //把起點加入開啟列表

　　　　loop{

　　　　　　currentNode = lowest f cost in openList；//把開啟列表中f值最低的節點作為當前節點

　　　　　　if (currentNode == end) return; //找到路線

　　　　　　foreach(neighbour in currentNode.Neighbours){ //對所有當前節點的相鄰節點進行迴圈

　　　　　　　　if (closeList.Contains(neighbour) or neighbour == obstacle ) continue; //跳過關閉列表中的節點和障礙物節點

　　　　　　　　if( new fCost <= old fCost || !openList.Contains(neighbour) ){ //如果新節點的f值小於老節點的f值，用新節點替換老節點

　　　　　　　　　　neighbour.fCost = new fCost;

　　　　　　　　　　neighbour.parent = currentNode;

　　　　　　　　　　if(!openList.Contains(neighbour)) openList.Add(neighbour);//如果新節點不在開啟列表，將其加入開啟列表

　　　　　　　　}

二、演算法實現

首先，在路徑網格中每一個網格都有一個對應的坐標，因此我創建了一個Point2類用來表示網格坐標

 1 //A class used to store the position information
 2 public class Point2
 3 {
 4     public Point2(int x, int y)
 5     {
 6         this.x = x;
 7         this.y = y;
 8     }
 9 
10     public int x { get; set; }
11 
12     public int y { get; set; }
13 
14     public override bool Equals(object obj)
15     {
16         return this.x == (obj as Point2).x && this.y == (obj as Point2).y;
17     }
18 
19     public override int GetHashCode()
20     {
21         return x ^ (y * 256);
22     }
23 
24     public override string ToString()
25     {
26         return x + "," + y;
27     }
28 
29     public static bool operator ==(Point2 a, Point2 b)
30     {
31         return a.Equals(b);
32     }
33 
34     public static bool operator !=(Point2 a, Point2 b)
35     {
36         return !a.Equals(b);
37     }
38 }

View Code

　　接下來，我創建了一個PathNode類用來記錄單個節點的信息

 1 public class PathNode
 2 {
 3     public PathNode(bool isWall, Point2 position)
 4     {
 5         this.isWall = isWall;
 6         this.position = position;
 7     }
 8 
 9     public readonly Point2 position;
10 
11     public bool isWall { get; set; }
12 
13     public PathNode parent { get; set; }
14 
15     public int gCost { get; set; }
16 
17     public int hCost { get; set; }
18 
19     public int fCost {
20         get {
21             return gCost + hCost;
22         }
23     }
24 
25     public override bool Equals(object obj)
26     {
27         PathNode node = obj as PathNode;
28         return node.isWall == this.isWall && node.gCost == this.gCost && node.hCost == this.hCost && node.parent == this.parent && this.position == node.position;
29     }
30 
31     public override int GetHashCode()
32     {
33         return gCost ^ (hCost * 128) + position.GetHashCode();
34     }
35 
36     public static bool operator ==(PathNode a, PathNode b)
37     {
38         return a.Equals(b);
39     }
40 
41     public static bool operator !=(PathNode a, PathNode b)
42     {
43         return !a.Equals(b);
44     }
45 }

View Code

　　最後是我們的PathGrid類，通過創建該類的實例來創建一個網格信息，其中包含了網格大小以及所有障礙物信息。使用中輸入起點信息和終點信息可以返迴路徑信息。關於代碼部分，由於Astar演算法中開銷最大的部分是開啟列表和關閉列表的維護以及在開啟列表中尋找f值最低的部分。因此我用C#的SortedDictionary額外創建了一個開啟列表用於查詢f值最低的節點。當然演算法還存在很大的優化空間，不過像32*32這樣的小的網格中已經夠用了。

  1 using System.Collections.Generic;
  2 using System.Linq;
  3 using System;
  4 
  5 public class PathGrid
  6 {
  7     private SortedDictionary<int, List<Point2>> openTree = new SortedDictionary<int, List<Point2>>();
  8 
  9     private HashSet<Point2> openSet = new HashSet<Point2>();
 10     private HashSet<Point2> closeSet = new HashSet<Point2>();
 11     private Dictionary<Point2, PathNode> allNodes = new Dictionary<Point2, PathNode>();
 12 
 13     private Point2 endPos;
 14     private Point2 gridSize;
 15 
 16     private List<Point2> currentPath;
 17 
 18     //這一部分在實際尋路中並不需要，只是為了方便外部程式實現尋路可視化
 19     public HashSet<Point2> GetCloseList()
 20     {
 21         return closeSet;
 22     }
 23 
 24     //這一部分在實際尋路中並不需要，只是為了方便外部程式實現尋路可視化
 25     public HashSet<Point2> GetOpenList()
 26     {
 27         return openSet;
 28     }
 29 
 30     //這一部分在實際尋路中並不需要，只是為了方便外部程式實現尋路可視化
 31     public List<Point2> GetCurrentPath()
 32     {
 33         return currentPath;
 34     }
 35 
 36     //新建一個PathGrid，包含了網格大小和障礙物信息
 37     public PathGrid(int x, int y, List<Point2> walls)
 38     {
 39         gridSize = new Point2(x, y);
 40         for (int i = 0; i < x; i++) {
 41             for (int j = 0; j < y; j++) {
 42                 Point2 newPos = new Point2(i, j);
 43                 allNodes.Add(newPos, new PathNode(walls.Contains(newPos), newPos));
 44             }
 45         }
 46     }
 47 
 48     //尋路主要邏輯，通過調用該方法來獲取路徑信息，由一串Point2代表
 49     public List<Point2> FindPath(Point2 beginPos, Point2 endPos)
 50     {
 51         List<Point2> result = new List<Point2>();
 52 
 53         this.endPos = endPos;
 54         Point2 currentPos = beginPos;
 55         openSet.Add(currentPos);
 56 
 57         while (!currentPos.Equals(this.endPos)) {
 58             UpdatePath(currentPos);
 59             if (openSet.Count == 0) return null;
 60 
 61             currentPos = openTree.First().Value.First();
 62         }
 63 
 64         Point2 path = currentPos;
 65 
 66         while (!path.Equals(beginPos)) {
 67             result.Add(path);
 68             path = allNodes[path].parent.position;
 69             currentPath = result;
 70         }
 71 
 72         result.Add(beginPos);
 73         return result;
 74     }
 75 
 76     //尋路
 77     private void UpdatePath(Point2 currentPos)
 78     {
 79         closeSet.Add(currentPos);
 80         RemoveOpen(currentPos, allNodes[currentPos]);
 81         List<Point2> neighborNodes = FindNeighbor(currentPos);
 82         foreach (Point2 nodePos in neighborNodes) {
 83 
 84             PathNode newNode = new PathNode(false, nodePos);
 85             newNode.parent = allNodes[currentPos];
 86 
 87             int g;
 88             int h;
 89 
 90             g = currentPos.x == nodePos.x || currentPos.y == nodePos.y ? 10 : 14;
 91 
 92             int xMoves = Math.Abs(nodePos.x - endPos.x);
 93             int yMoves = Math.Abs(nodePos.y - endPos.y);
 94 
 95             int min = Math.Min(xMoves, yMoves);
 96             int max = Math.Max(xMoves, yMoves);
 97             h = min * 14 + (max - min) * 10;
 98 
 99 
100             newNode.gCost = g + newNode.parent.gCost;
101             newNode.hCost = h;
102 
103             PathNode originNode = allNodes[nodePos];
104 
105             if (openSet.Contains(nodePos)) {
106                 if (newNode.fCost < originNode.fCost) {
107                     UpdateNode(newNode, originNode);
108                 }
109             } else {
110                 allNodes[nodePos] = newNode;
111                 AddOpen(nodePos, newNode);
112             }
113         }
114     }
115 
116     //將舊節點更新為新節點
117     private void UpdateNode(PathNode newNode, PathNode oldNode)
118     {
119         Point2 nodePos = newNode.position;
120         int oldCost = oldNode.fCost;
121         allNodes[nodePos] = newNode;
122         List<Point2> sameCost;
123 
124         if (openTree.TryGetValue(oldCost, out sameCost)) {
125             sameCost.Remove(nodePos);
126             if (sameCost.Count == 0) openTree.Remove(oldCost);
127         }
128 
129         if (openTree.TryGetValue(newNode.fCost, out sameCost)) {
130             sameCost.Add(nodePos);
131         } else {
132             sameCost = new List<Point2> { nodePos };
133             openTree.Add(newNode.fCost, sameCost);
134         }
135     }
136 
137     //將目標節點移出開啟列表
138     private void RemoveOpen(Point2 pos, PathNode node)
139     {
140         openSet.Remove(pos);
141         List<Point2> sameCost;
142         if (openTree.TryGetValue(node.fCost, out sameCost)) {
143             sameCost.Remove(pos);
144             if (sameCost.Count == 0) openTree.Remove(node.fCost);
145         }
146     }
147 
148     //將目標節點加入開啟列表
149     private void AddOpen(Point2 pos, PathNode node)
150     {
151         openSet.Add(pos);
152         List<Point2> sameCost;
153         if (openTree.TryGetValue(node.fCost, out sameCost)) {
154             sameCost.Add(pos);
155         } else {
156             sameCost = new List<Point2> { pos };
157             openTree.Add(node.fCost, sameCost);
158         }
159     }
160 
161     //找到某節點的所有相鄰節點
162     private List<Point2> FindNeighbor(Point2 nodePos)
163     {
164         List<Point2> result = new List<Point2>();
165 
166         for (int x = -1; x < 2; x++) {
167             for (int y = -1; y < 2; y++) {
168                 if (x == 0 && y == 0) continue;
169 
170                 Point2 currentPos = new Point2(nodePos.x + x, nodePos.y + y);
171 
172                 if (currentPos.x >= gridSize.x || currentPos.y >= gridSize.y || currentPos.x < 0 || currentPos.y < 0) continue; //out of bondary
173                 if (closeSet.Contains(currentPos)) continue; // already in the close list
174                 if (allNodes[currentPos].isWall) continue;  // the node is a wall
175 
176                 result.Add(currentPos);
177             }
178         }
179 
180         return result;
181     }
182 }

View Code