K：哈弗曼樹

相關介紹:

 樹形結構除了應用於查找和排序等操作時能調高效率，它在信息通訊領域也有著廣泛的應用。哈弗曼(Huffman)樹就是一種在編碼技術方面得到廣泛應用的二叉樹，它同時也是一種最優二叉樹。

哈弗曼樹相關的的基本概念:

 為了給出哈弗曼樹的定義，從以下幾個基本概念出發併進行描述。

1. 節點間的路徑和節點的路徑長度：所謂節點間的路徑是指一個節點到另一個節點所經歷的節點和分支序列。節點的路徑長度是指從根節點到該節點間的路徑上的分支數目。

2. 節點的權和節點的帶權路徑：在實際應用中，人們往往會給樹中的每一個節點賦予一個具有某種實際意義的數值，這個數值稱為節點的權值。節點的帶權路徑長度就是該節點的路徑長度與該節點的權值的乘積。

3. 樹的帶權路徑長度：樹的帶權路徑長度就是樹中所有葉節點的帶權路徑長度之和，通常記為：\(WPL=\sum_{i=1}^{n}W_{i} \times L_{i}\)其中，n為葉節點的個數，\(W_{i}\)為第i個葉節點的權值，\(L_{i}\)為第i個葉節點的路徑長度

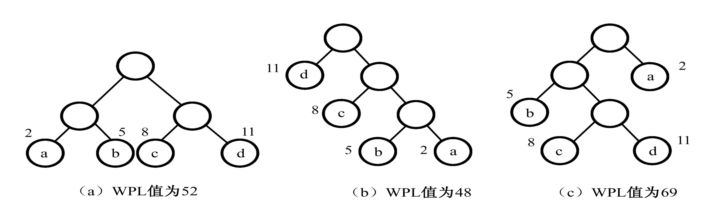
4. 最優二叉樹：給定n個權值並作為n個葉節點按一定規則構造一棵二叉樹，使得其帶權路徑長度達到最小值，則這棵二叉樹被稱為最優二叉樹。下圖展示了具有不同帶權路徑長度的二叉樹，其中，第二棵樹為最優二叉樹

哈弗曼樹和哈弗曼編碼的構造方法

 哈弗曼樹的構造步驟如下所示:

 假設n個葉節點的權值分別為{w1,w2,...,wn},則

1. 由已知給定的n個權值{w1,w2,w3,...,wn},構造一個由n棵二叉樹所構成的森林F={T1，,T2,T3,...,Tn}，其中每一棵二叉樹只有一個根節點，並且根節點的權值分別為w1，w2，....，wn

2. 在二叉樹森林F中選取根節點的權值最小和次小的兩棵二叉樹，分別把它們作為左子樹和右子樹去構造一棵新二叉樹，新二叉樹的根節點權值為其左、右子樹根節點的權值之和

3. 作為新二叉樹的左右子樹的兩棵二叉樹從森林F中刪除。將新產生的二叉樹加入到森林F中

4. 重覆步驟2和步驟3，直到森林中只剩下一棵二叉樹為止，則這棵二叉樹就是所構成的哈弗曼樹

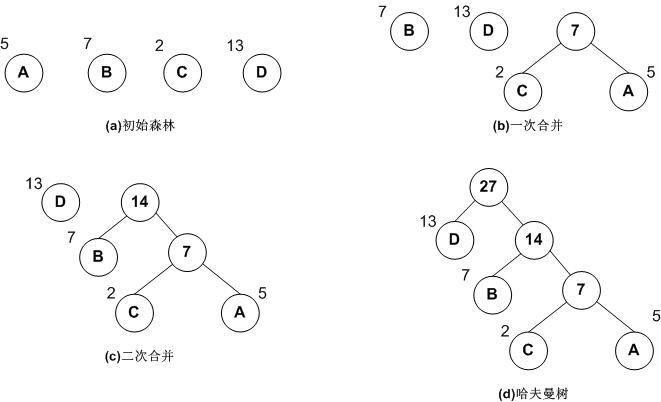
下圖展示了哈弗曼樹的構造過程:

哈弗曼樹構造過程的代碼實現

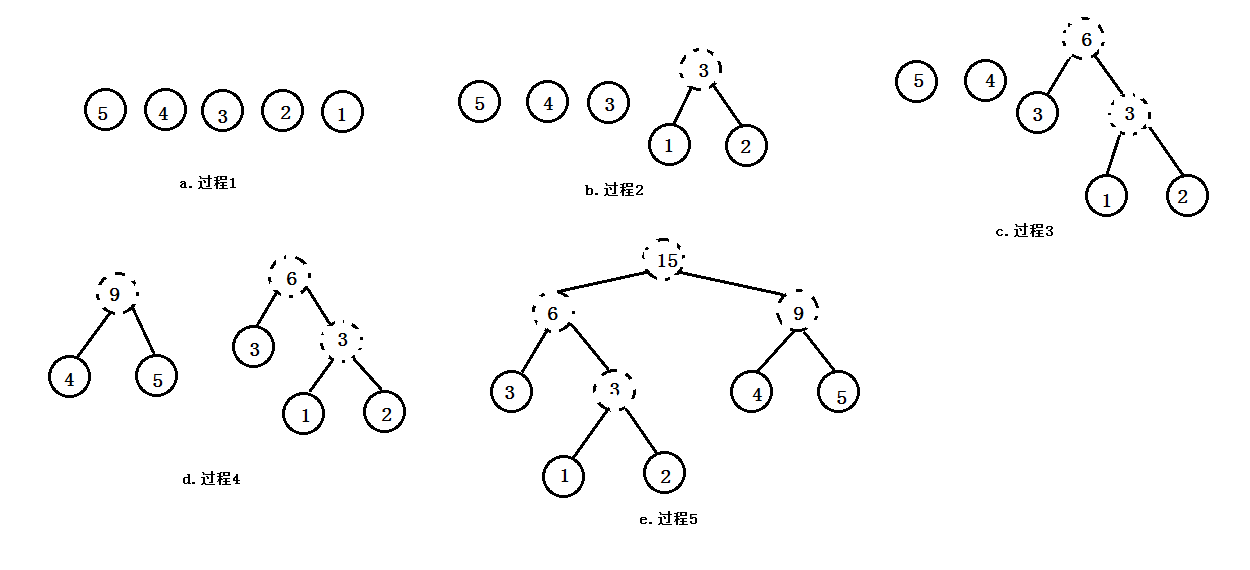
 以下其代碼演示了哈弗曼樹的構造實現其中，測試代碼所用的圖如下所示:

相關代碼:

package all_in_tree;

import java.util.Comparator;
import java.util.LinkedList;
import java.util.PriorityQueue;
import java.util.Queue;

/**
 * 該類用於演示哈弗曼樹的構造過程
 * @author 學徒
 *
 */
public class Huffman
{
    //哈弗曼樹的根節點
    private HuffmanNode root;
    //一個優先順序隊列，確保每次取出的均為節點中其權值最小的節點
    private Queue<HuffmanNode> q;
    /**
     * 用於初始化，其優先隊列
     */
    public Huffman()
    {
        Comparator<HuffmanNode> cmp=new Comparator<HuffmanNode>()
        {
                @Override
                public int compare(HuffmanNode obj1,HuffmanNode obj2)
                {
                    int obj1Number=obj1.weight;
                    int obj2Number=obj2.weight;
                    if(obj1Number>obj2Number)
                        return 1;
                    else if(obj1Number<obj2Number)
                        return -1;
                    else
                        return 0;
                }
        };
        q=new PriorityQueue<HuffmanNode>(11,cmp);
    }
    /**
     * 用於添加節點到優先隊列中，進行哈弗曼樹的構造
     * @param node
     */
    public void addHuffmanNode(HuffmanNode node)
    {
        q.add(node);
    }
    /**
     * 用於構造哈弗曼樹
     */
    public HuffmanNode createHuffmanTree()
    {
        while(!q.isEmpty()&&q.size()>=2)
        {
            HuffmanNode node1=q.poll();
            HuffmanNode node2=q.poll();
            HuffmanNode newNode=new HuffmanNode();
            newNode.weight=node1.weight+node2.weight;
            newNode.left=node1;
            newNode.right=node2;
            q.add(newNode);
        }
        if(!q.isEmpty())
            this.root=q.poll();
        return this.root;
    }
    /**
     * 用於測試相關的代碼
     */
    public static void main(String[] args)
    {
        Huffman tree=new Huffman();
        for(int i=0;i<5;i++)
        {
            tree.addHuffmanNode(new HuffmanNode((char)('A'+i),i+1));
        }
        HuffmanNode root=tree.createHuffmanTree();
        System.out.println("其最高頂點的權值"+root.weight);
        //對該哈弗曼樹進行層次遍歷
        Queue<HuffmanNode> q=new LinkedList<HuffmanNode>();
        q.add(root);
        while(!q.isEmpty())
        {
            HuffmanNode node=q.poll();
            System.out.print(node.weight+"\t");
            if(node.left!=null)
                q.add(node.left);
            if(node.right!=null)
                q.add(node.right);
        }
    }
}
/**
 * 用於創建哈弗曼樹的節點類的描述
 * @author 學徒
 *
 */
class HuffmanNode
{
    //用於存放相關的數據
    Object data;
    //用於記錄該節點的權
    int weight;
    //該節點的左孩子
    HuffmanNode left;
    //該節點的右孩子
    HuffmanNode right;
    public HuffmanNode()
    {
    }
    public HuffmanNode(Object data,int weight)
    {
        this.data=data;
        this.weight=weight;
    }
}

運行結果:

其最高頂點的權值15
15  6   9   3   3   4   5   1   2   

回到目錄|·(工)·）