MATLAB求解二重積分案例

凱魯嘎吉 - 博客園

http://www.cnblogs.com/kailugaji/

  定積分解決的是一維連續量求和的問題，而解決多維連續量的求和問題就要用到重積分了。重積分是建立在定積分的基礎上的，它的基本思想也是將重積分化為定積分來計算，其中關鍵是積分限的確定，這也是重積分的難點所在。正是因為重積分從計算上來說仍是使用的定積分的方法，MATLAB系統並沒有提供專門的命令函數來處理重積分，因此在我們確定了積分限後仍是使用int()命令來處理重積分問題。有些積分區間形狀比較複雜，為了方便表達積分的上下限常常把比較複雜的區間分割成若幹個相對簡單的區間，然後對不同的區間分別積分，最後把各個積分結果相加起來。

計算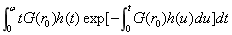

其中，

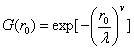
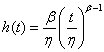
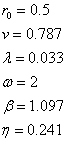
wrr.m:

function tt=wrr(r,v,c,b,y,w)
syms u t
p=-(r/c)^v;
g=exp(p);
h=(b/y)*(t/y)^(b-1);
hu=(b/y)*(u/y)^(b-1);
f=int(g*hu,u,0,t);
tt=int(t*g*h*exp(-f),t,0,w);
tt=vpa(tt,10);

//結果為：
>> clear
>> tt=wrr(0.5,0.787,0.033,1.097,0.241,2)
 
tt =
 
0.002183207532

對於二元函數的符號積分，可以先轉化成逐次積分形式，利用int函數進行求解。