數據結構---哈希表（散列表）

我們在Java容器中談到：有哈希表（也稱為散列表）支持的HashMap、LinkedHashSet等都具有非常高的查詢效率。這其中就是Hash起的作用。順序查找的時間複雜度為O(N) ,二分查找和查找樹的時間複雜度為O(logN)，而 哈希表的時間複雜度為O(1) 。不過這隻是理想狀態，實際並不那麼完美。

1.哈希表的概念和思想 

哈希表是唯一的專用於集合的數據結構。可以以常量的平均時間實現插入、刪除和查找。

哈希表的思想是：用一個與集合規模差不多大的數組來存儲這個集合，將數據元素的關鍵字映射到數組的下標，這個映射稱為“散列函數”，數組稱為“散列表”。查找時，根據被查找的關鍵字找到存儲數據元素的地址，從而獲取數據元素。

由於任何類型的數據都能轉化為一個整數型，我們假設所有的數據元素的關鍵字都是較小的非負整數，就可以用一個簡單的數組Data保存這個集合，數據類型就是集合中的元素的類型。

開始時，給數組的每個元素賦空值，NULL。當要在集合中插入一個關鍵字為Key的數據元素時，就檢查Data[Key]是否為空。如果為空，則吧插入的元素存儲在Data[Key]中；如果不為空，則表示遇到重覆元素，插入失敗。

當要查找某個數據元素時，只需要根據查找的關鍵字Key直接取出Data[Key]的值，如果Data[Key]的值為空，則表示關鍵字對應的元素不存在。否則，Data[Key]就是要查找的元素。刪除時，只需要將對應數組的元素設為NULL即可。每種操作的時間為一個常量。

散列函數函數的應用帶來一個複雜的問題：

因為散列函數的定義域範圍比值域大，兩個或更多的數據元素可能被映射到同一個位置，稱為“衝突或碰撞”。這種情況是不可避免的。因此，實現散列表的兩個最基本的問題是：如何設計散列函數，如何解決碰撞。

2.散列函數

在散列表中。插入、刪除和查找都會用到散列函數。散列函數的計算速度直接影響散列表的性能。好的散列函數的一個標準就是：計算速度快。另一點就是：結點的散列地址儘可能均勻。使得衝突的機會儘可能少。

常用的散列函數包括直接定址法、保留餘數法、數字分析法、平方取中法和摺疊法等。

(1)直接定址法

直接取關鍵字的值或關鍵字的某個線性函數的值作為散列地址。設關鍵字為x，那麼散列地址可表示為：

                                                               H(x) = x 或  H(x) = ax + b （a、b為常數）

例如：關鍵字集合為{100, 400，600， 200， 800， 900}，利用直接定址法，若選取散列函數為H(x) = x/100,則散列表如下：

(2)保留餘數法

如果M是散列表的大小，關鍵字 x 的數據元素的散列地址為：H(x) = x mod M

在保留餘數法中，選取合適的餘數M很重要，如果選取不當，則導致大量的碰撞。

經驗表明：M為素數（除了1和它本身以外不再有其他因數。）時，散列表的分佈比較均勻。

(3)數字分析法

在某些領域，關鍵字之間的區別集中在某些位上面，例如電腦的IP地址，一個IP地址由兩部分組成：網路號和主機號。在同一子網中的主機的網路號是相同的。在某個網路中，我們可以將IP地址作為關鍵字。如果採取散列方法保存這個集合，可以選取IP地址的主機號部分作為存儲地址。

更一般的說，如果在關鍵字集合中，每個關鍵字均由n位組成，分析關鍵字中每一位的分佈規律，並從中提取分佈均勻的若幹位或它們的組合作為地址。

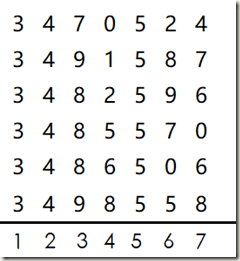
例如：右邊的數據 第一列、第二列、第五列 對於不是區分關鍵字沒有價值。 第三列只有 7 、 8 、9 三種數字。 餘下的幾列比較均勻，可作為散列表的地址選用。 若散列表的地址是三位，直接選取剩下的三位即可； 若散列表的地址小於三位。則選擇其他方法，比如：保留餘數法等等 將三位關鍵字映射到一個更小的值域中。

(4)平方取中法

如果關鍵字中的各位的分佈都比較均勻，但關鍵字的值域比數組的規模大，則可以將關鍵字平方後，取其結果中間各位作為散列函數值。

由於中間各位和每一位數字有關係，因此均勻分佈的可能性較大。

例如：4731 X 4731 = 22 382 361.中間選取幾位，依賴於散列表的單元總數。若散列表中有100個單位，選取中間4,5兩位，即關鍵字

4731的地址為82.

(5)摺疊法

如果關鍵字相當長，以至於和散列表的單元總數相比大的多，則採取摺疊法。如果數字的分佈大體上是均勻的，通常選取一個長度後，將關鍵字按長度分組相加。例如：542 242 241，摺疊後542 + 242 + 241 = 1025，拋棄進位，得到散列表的結果為25.

不存在一種萬能的散列函數，在任何情況下都是出色的。但是大部分情況下，保留餘數法比較好。

實際中選取散列函數需要考慮的因素有：

• 計算散函數所需時間。
• 關鍵字長度。
• 散列表長度（散列表地址範圍）。
• 關鍵字分佈情況。
• 記錄的查找頻率。

3.碰撞的解決

在選取散列函數時，由於很難選取一個既均勻分佈又簡單，同時保證關鍵字和散列地址一一對應的散列表，所以衝突時不可避免的。如果具有不同關鍵字的 k 個數據元素的散列地址完全相同，就必須為 k-1個數據元素重新分配存儲單元。通常稱其為“溢出”的數據元素。

常用的處理衝突的方法有兩種：

(1)將溢出的數據元素存放到散列表中沒有使用的單元中。

這種方法是“封閉”的，不需要使用額外的存儲單元，稱為“閉散列表”。具體的實施方案有：線性探針法、二次探測發、再散列法。

• 線性探針法：在數組中從映射到的位置開始順序查找空位置，如果需要，從最後一個位置繞回第一個位置。這種方法碰撞可能引起連鎖反應，使表中形成一些較長的連續被占用的單元，如：從1---10的地址全部被使用。從而使散列表的性能降低。
• 二次探測發：不直接檢查下一個單元，而是檢查遠離初始探測點的某一單元，以消除線性探測法中的初始聚集的問題.
• 再散列法：有兩個散列函數H1和H2。H1用來計算探測序列的起始地址，H2用來計算下一個位置的步長。第二個散列函數必須仔細選擇。例如，它永遠不能計算出0，必須保證所有單元能夠探測到。

(2)將映射到同一地址的數據元素分別保存到散列表以外的各自線性表中。

由於地址相同的數據元素個數變化比較大，因此通常採用鏈表的方式。散列表本身只保存一個指向各自鏈表中第一個節點的指針。這種方法稱為“開散列表"，或拉鏈法，可以理解為“鏈表的數組”。

開散列表將具有同一散列地址的數據元素都存儲在一個單鏈表中。在散列表中插入、查找或刪除一個元素，就是在對應的單鏈表中進行的。為了方便操作，將單鏈表設計為帶頭結點的單鏈表。

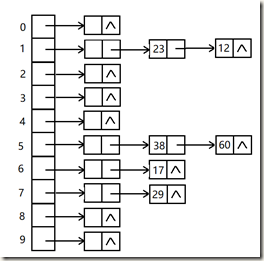
例如；一個規模為11的開散列表中依次插入關鍵字17、21、23、60、29、38......,散列函數為

H（Key）= key mod 11，散列表如下：

在開散列表中，插入、刪除和查找操作的實現都相當簡單。 插入x時，首先計算H(x),將x插入到H(x)指向的單鏈表的表頭。 查找時，也是先計算H(x),然後順序查找H(x)指向的單鏈表。 刪除操作同樣簡單，先計算H(x)，然後順序查找H(x)指向的單鏈表， 找到x後刪除

2018-01-05