CPP--正碼，反碼，補碼~附整數溢出的探討

 之前說到了long的爭議（http://www.cnblogs.com/dotnetcrazy/p/8059210.html），這邊就不用long來舉例了，用int吧

可以看一下這篇文章（http://www.cnblogs.com/dotnetcrazy/p/6743530.html），更好理解本文（本文不繼續探討大小端對齊問題，只研究標題內容）

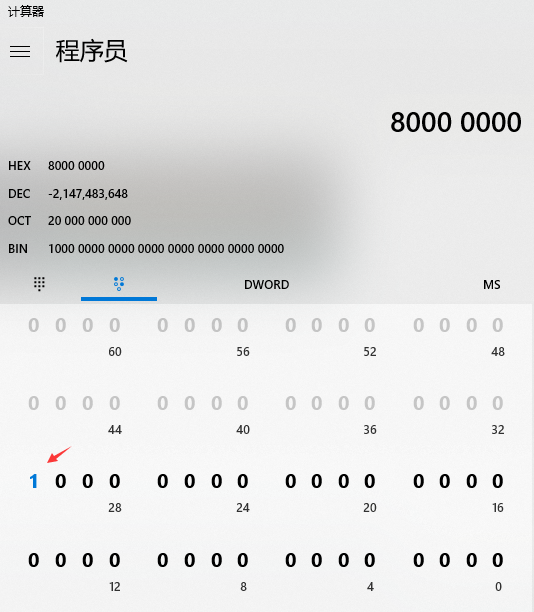
1.基礎就不詳解了貼張圖：

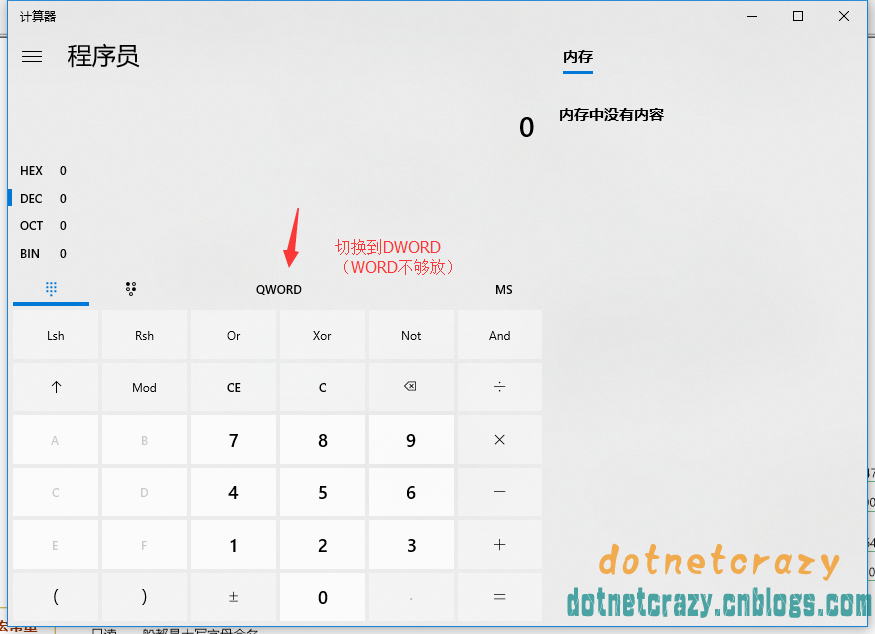
說一下QWORD，之前也被網上誤導了，網上很多都是說無符號的word，按照慣例，如果是unsigned word，那麼所占位元組應該和word一樣才對

驗證：有無符號，他所占位元組並不變

後來發現Win10最新版有一計算器神器（你們可以通過應用商城裝）===》

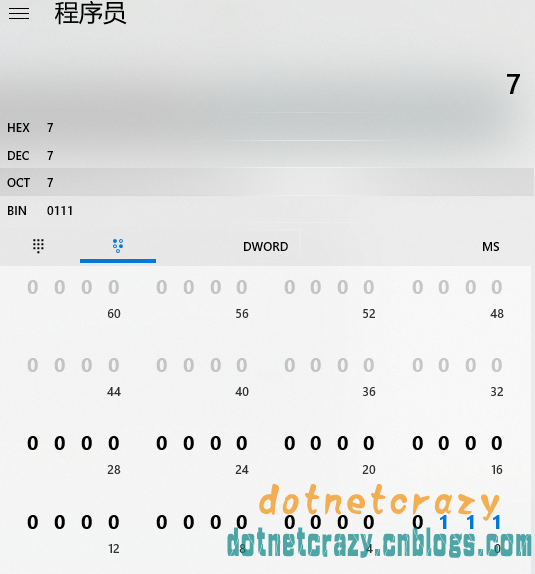
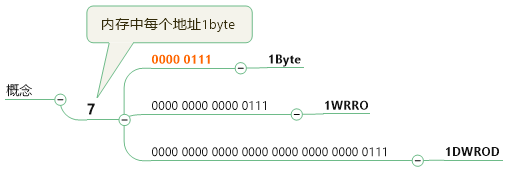
通過7來說說這些“字”寶寶們（我後面說補碼計算的時候也會用到這個案例）

1Byte=8bit（一個二進位位就是一個bit）

7==》0000 0111

1WORD=2Byte，7==》0000 0000 0000 0111

1DWORD=4Byte，7==》0000 0000 0000 0000 0000 0000 0000 0111

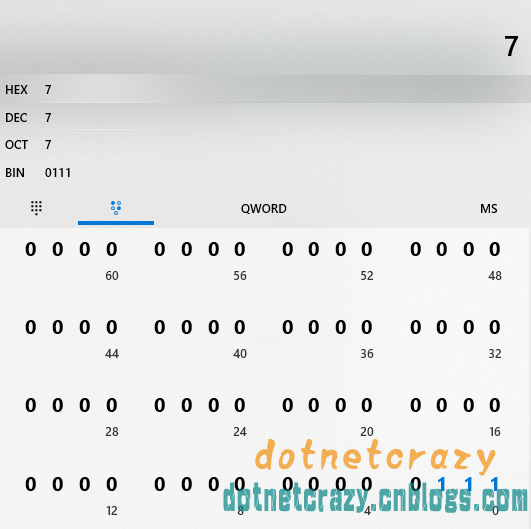
重點來了，要是QWORD真的是WORD無符號字，那麼應該和WORD一樣只占2Byte

然而事實==》打臉打的PaPa響，1QWORD=8Byte，7==》以下省略一千字

2.原碼，反碼，補碼

在電腦內，有符號數有3種表示法：原碼、反碼和補碼

原碼：電腦中對數字的二進位定點表示方法。最高位為符號位（正數該位為0，負數該位為1）其餘位表示數值的大小 

反碼：正數的反碼與其原碼相同，負數的反碼：符號位不動，其他取反

補碼：正數的補碼和原碼相同，負數的補碼：符號位不動，其他取反，最後+1（相當於：補碼+1）

補碼的好處：使符號位能與有效值部分一起參加運算,從而簡化運算規則；使符號位能與有效值部分一起參加運算,從而簡化運算規則

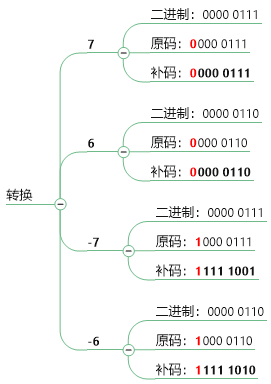
來張圖更直觀：

來來來，實踐驗證一下：

分析：按照求負數補碼的逆過程，數值部分應是最低位減1，然後取反。
但是對二進位數來說，先減1後取反和先取反後加1得到的結果是一樣的，故仍可採用取反加1 的方法。

這些都比較簡單，下麵說下補碼的好處：

 

體驗分析一下

7-6=1；-7+6=-1

7-6=1

 7補碼：0000 0111

-6補碼：1111 1010

  0000 0111
  1111 1010
  ---------
1 0000 0001

進位捨棄（總共就8位，溢出就沒了），0000 0001==>1（正數的補碼是他本身）

-7+6=-1

-7補碼：1111 1001

 6補碼：0000 0110

1111 1001
0000 0110
---------
1111 1111

木有進位，補碼：1111 1111，正碼（符號位不動，其他取反，最後+1）：1000 0001==>-1

擴展（有興趣的可以自己研究一下補碼的各種溢出）：https://baike.baidu.com/item/反碼#5

3.整數溢出探討

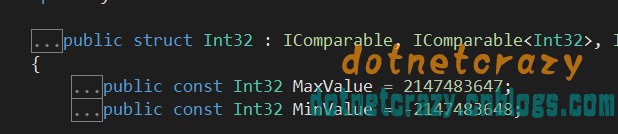
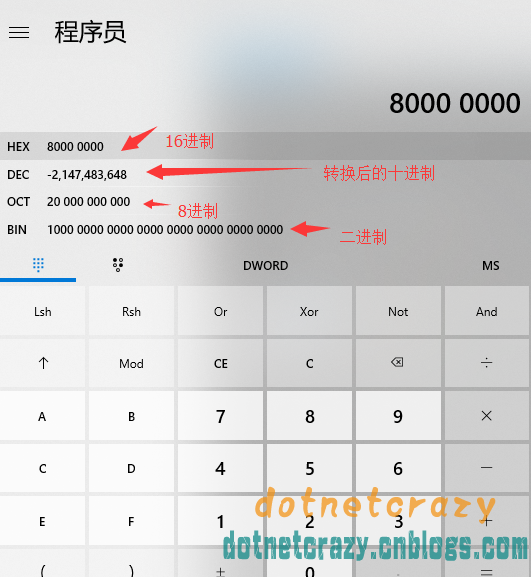
 intmax=0x7FFFFFFF; （2147483647）

不清楚的可以看這個圖，第一位是符號位，後面是數值部分，所以第一個最大是7，其他最大是F

借用Net裡面的Int.Max驗證下：2147483647

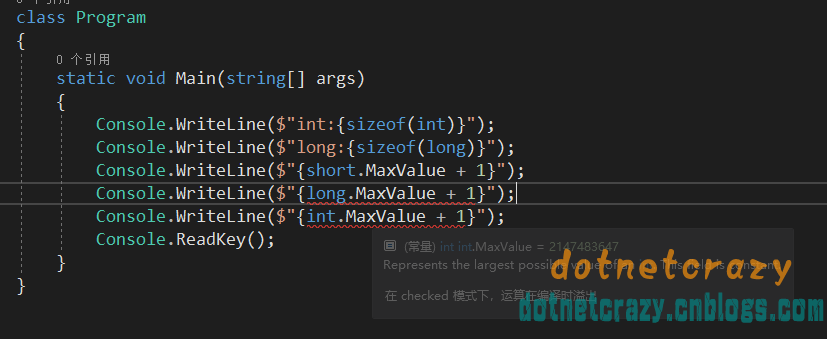
不高興搞需的，畢竟不是學生了，直接跑個程式看看

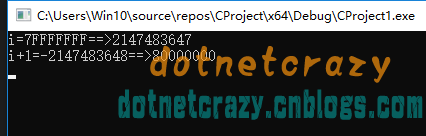
int main() {
 int i = 0x7fffffff;
 printf("i=%X==>%d\n", i, i);
 i += 1;
 printf("i+1=%d==>%X\n", i, i);
 return 0;
}

CentOS_X64：i+1=-2147483648==>0x80000000

Win10_X64：i+1=-2147483648==>0x80000000

記得以前學生時代就很不解，老師也說不清楚，這次看見了就研究了下

來來來，Net來個福利：自己研究下為啥

不扯了，二進位走一個：

0111 1111 1111 1111  1111 1111 1111 1111
                                       +1
1000 0000 0000 0000  0000 0000 0000 0000
———— ———— ———— ————  ———— ———— ———— ————
 8    0    0    0     0    0    0     0

 intmax+1=0x80000000，程式員還是比較喜歡十六進位啊~方便

可能你還沒轉過來，(⊙o⊙)…，好吧，我們用補碼的方式再算一遍

0111 1111 1111 1111  1111 1111 1111 1111
0000 0000 0000 0000  0000 0000 0000 0001
---- ---- ---- ----  ---- ---- ---- ----
1000 0000 0000 0000  0000 0000 0000 0000

轉為正碼：
1000 0000 0000 0000 0000 0000 0000 0000 補碼
1111 1111 1111 1111 1111 1111 1111 1111 正碼

2^31==>2147483648，符號位是1，則最後結果是-2147483648

------------------------------------------

收工了，感興趣的可以用Win10計算神器看看（用QWORD又是怎樣呢，可以自己思考，很有意思哦）

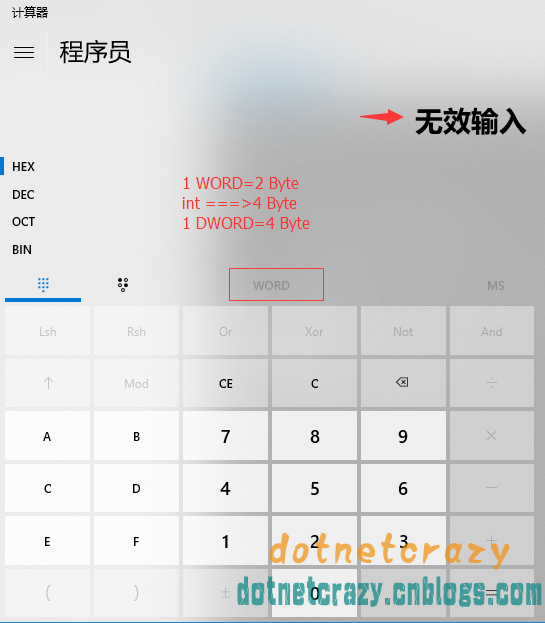
稍微解釋一下：word是2Byte，intmax是4Byte，所以不夠放

在選下HEX，輸入運算得到的數字