樹鏈剖分詳解

来源:http://www.cnblogs.com/zwfymqz/archive/2017/12/24/8094500.html
-Advertisement-
Play Games

前言 樹鏈剖分是什麼？ 樹鏈剖分，說白了就是一種讓你代碼不得不強行增加1k的數據結構-dms 個人理解：+1:joy: 有什麼用？ 證明出題人非常毒瘤 可以非常友(bao)好(li)的解決一些樹上問題:grimacing: （友情提示：學樹鏈剖分之前請先掌握線段樹） 核心思想 樹鏈剖分的思想比較神奇 ...


前言

  • 樹鏈剖分是什麼？

樹鏈剖分，說白了就是一種讓你代碼不得不強行增加1k的數據結構-dms

　　個人理解：+1:joy:

  • 有什麼用？

證明出題人非常毒瘤

可以非常友(bao)好(li)的解決一些樹上問題:grimacing:

（友情提示：學樹鏈剖分之前請先掌握線段樹）

核心思想

樹鏈剖分的思想比較神奇

它的思想是：把一棵樹拆成若幹個不相交的鏈，然後用一些數據結構去維護這些鏈

 

那麼問題來了

  •  如何把樹拆成鏈？

首先明確一些定義

重兒子：該節點的子樹中,節點個數最多的子樹的根節點(也就是和該節點相連的點)，即為該節點的重兒子

重邊：連接該節點與它的重兒子的邊

重鏈：由一系列重邊相連得到的鏈

輕鏈：由一系列非重邊相連得到的鏈

這樣就不難得到拆樹的方法

對於每一個節點，找出它的重兒子，那麼這棵樹就自然而然的被拆成了許多重鏈與許多輕鏈

  •  如何對這些鏈進行維護？

首先，要對這些鏈進行維護，就要確保每個鏈上的節點都是連續的，

因此我們需要對整棵樹進行重新編號，然後利用dfs序的思想，用線段樹或樹狀數組等進行維護（具體用什麼需要看題目要求，因為線段樹的功能比樹狀數組強大，所以在這裡我就不提供樹狀數組的寫法了）

 註意在進行重新編號的時候先訪問重鏈

這樣可以保證重鏈內的節點編號連續

 

上面說的太抽象了，結合一張圖來理解一下

對於一棵最基本的樹

 

給他標記重兒子，

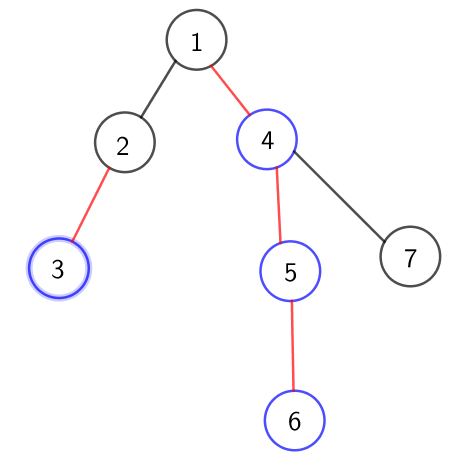 藍色為重兒子，紅色為重邊

然後對樹進行重新編號

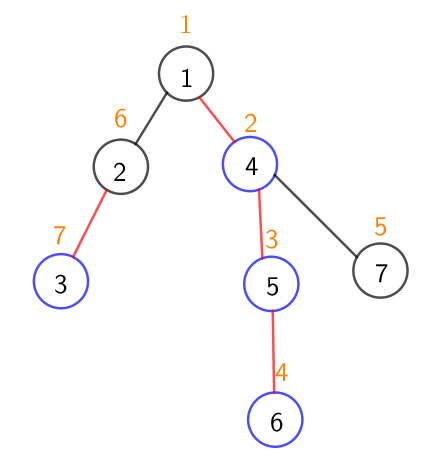橙色表示的是該節點重新編號後的序號

不難看出重鏈內的節點編號是連續的

 

 

然後就可以線上段樹上搞事情啦

像什麼區間加區間求和什麼的

另外有一個性質：以$i$為根的子樹的樹線上段樹上的編號為$[i,i+子樹節點數-1]$

 

接下來結合一道例題，加深一下對於代碼的理解

 

代碼

題目鏈接

樹鏈剖分的裸題

首先來一坨定義

 

int deep[MAXN];//節點的深度 
int fa[MAXN];//節點的父親 
int son[MAXN];//節點的重兒子 
int tot[MAXN];//節點子樹的大小

 

第一步

按照我們上面說的，我們首先要對整棵樹dfs一遍，找出每個節點的重兒子

順便處理出每個節點的深度，以及他們的父親節點

int dfs1(int now,int f,int dep)
{
    deep[now]=dep;
    fa[now]=f;
    tot[now]=1;
    int maxson=-1;
    for(int i=head[now];i!=-1;i=edge[i].nxt)
    {
        if(edge[i].v==f) continue;
        tot[now]+=dfs1(edge[i].v,now,dep+1);
        if(tot[edge[i].v]>maxson) maxson=tot[edge[i].v],son[now]=edge[i].v;
    }
    return tot[now];
}

 

第二步

然後我們需要對整棵樹進行重新編號

我把一開始的每個節點的權值存在了$b$數組內

void dfs2(int now,int topf)
{
    idx[now]=++cnt;
    a[cnt]=b[now];
    top[now]=topf;
    if(!son[now]) return ;
    dfs2(son[now],topf);
    for(int i=head[now];i!=-1;i=edge[i].nxt)
        if(!idx[edge[i].v])
            dfs2(edge[i].v,edge[i].v);
}

$idx$表示重新編號後該節點的編號是多少

另外，這裡引入了一個$top$數組，

$top[i]$表示$i$號節點所在重鏈的頭節點(最頂上的節點)

至於這個數組有啥用，後面再說

 

第三步

我們需要根據重新編完號的樹，把這棵樹的上每個點映射到線段樹上，

struct Tree
{
    int l,r,w,siz,f;
}T[MAXN];
void Build(int k,int ll,int rr)
{
    T[k].l=ll;T[k].r=rr;T[k].siz=rr-ll+1;
    if(ll==rr)
    {
        T[k].w=a[ll];
        return ;
    }
    int mid=(ll+rr)>>1;
    Build(ls,ll,mid);
    Build(rs,mid+1,rr);
    update(k);
}

另外線段樹的基本操作，

這裡就不詳細解釋了

直接放代碼

void update(int k)//更新
{
    T[k].w=(T[ls].w+T[rs].w+MOD)%MOD;
}
void IntervalAdd(int k,int ll,int rr,int val)//區間加
{
    if(ll<=T[k].l&&T[k].r<=rr)
    {
        T[k].w+=T[k].siz*val;
        T[k].f+=val;
        return ;
    }
    pushdown(k);
    int mid=(T[k].l+T[k].r)>>1;
    if(ll<=mid)    IntervalAdd(ls,ll,rr,val);
    if(rr>mid)    IntervalAdd(rs,ll,rr,val);
    update(k);
}
int IntervalSum(int k,int ll,int rr)//區間求和
{
    int ans=0;
    if(ll<=T[k].l&&T[k].r<=rr)
        return T[k].w;
    pushdown(k);
    int mid=(T[k].l+T[k].r)>>1;
    if(ll<=mid) ans=(ans+IntervalSum(ls,ll,rr))%MOD;
    if(rr>mid)  ans=(ans+IntervalSum(rs,ll,rr))%MOD;
    return ans;
}
void pushdown(int k)//下傳標記
{
    if(!T[k].f) return ;
    T[ls].w=(T[ls].w+T[ls].siz*T[k].f)%MOD;
    T[rs].w=(T[rs].w+T[rs].siz*T[k].f)%MOD;
    T[ls].f=(T[ls].f+T[k].f)%MOD;
    T[rs].f=(T[rs].f+T[k].f)%MOD;
    T[k].f=0;
}

 

第四步

我們考慮如何實現對於樹上的操作

樹鏈剖分的思想是:對於兩個不在同一重鏈內的節點,讓他們不斷地跳,使得他們處於同一重鏈上

那麼如何"跳”呢？

還記得我們在第二次$dfs$中記錄的$top$數組麽？

有一個顯然的結論：$x$到$top[x]$中的節點線上段樹上是連續的，

結合$deep$數組

假設兩個節點為$x$,$y$

我們每次讓$deep[top[x]]$與$deep[top[y]]$中大的(在下麵的)往上跳(有點類似於樹上倍增)

讓x節點直接跳到$top[x]$,然後線上段樹上更新

最後兩個節點一定是處於同一條重鏈的，前面我們提到過重鏈上的節點都是連續的，直接線上段樹上進行一次查詢就好

void TreeSum(int x,int y)//x與y路徑上的和
{
    int ans=0;
    while(top[x]!=top[y])
    {
        if(deep[top[x]]<deep[top[y]]) swap(x,y);
        ans=(ans+IntervalSum(1,idx[ top[x] ],idx[x]))%MOD;
        x=fa[ top[x] ];
    }
    if(deep[x]>deep[y]) swap(x,y);
    ans=(ans+IntervalSum(1,idx[x],idx[y]))%MOD;
    printf("%d\n",ans);
}
void TreeAdd(int x,int y,int val)//對於x,y路徑上的點加val的權值
{
    while(top[x]!=top[y])
    {
        if(deep[top[x]]<deep[top[y]]) swap(x,y);
        IntervalAdd(1,idx[ top[x] ],idx[x],val);
        x=fa[ top[x] ];
    }
    if(deep[x]>deep[y])    swap(x,y);
    IntervalAdd(1,idx[x],idx[y],val);
}

在樹上查詢的這一步可能有些抽象，我們結合一個例子來理解一下

還是上面那張圖，假設我們要查詢$3.6$這兩個節點的之間的點權合，為了方便理解我們假設每個點的點權都是$1$

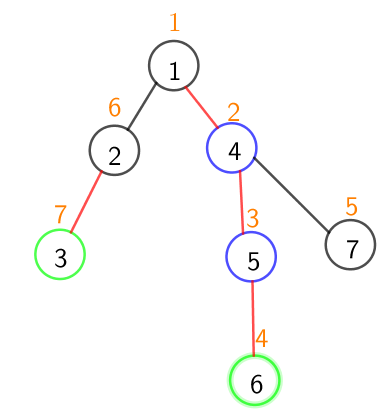
剛開始時

$top[3]=2,top[6]=1$

$deep[top[3]]=2,deep[top[6]]=1$

我們會讓$3$向上跳,跳到$top[3]$的爸爸,也就是$1$號節點

這是$1$號節點和$6$號節點已經在同一條重鏈內,所以直接對線段樹進行一次查詢即可

對於子樹的操作

這個就更簡單了

因為一棵樹的子樹線上段樹上是連續的

所以修改的時候直接這樣

IntervalAdd(1,idx[x],idx[x]+tot[x]-1,z%MOD);

 

時間複雜度

(剛開始忘記寫了,這一塊是後來補上的)

性質1

如果邊$\left( u,v\right)$,為輕邊,那麼$Size\left( v\right) \leq Size\left( u\right) /2$。

證明：顯然:joy:，否則該邊會成為重邊

性質2

樹中任意兩個節點之間的路徑中輕邊的條數不會超過$\log _{2}n$,重路徑的數目不會超過$\log _{2}n$

證明：不會:stuck_out_tongue_winking_eye:

 

有了上面兩條性質，我們就可以來分析時間複雜度了

由於重路徑的數量的上界為$\log _{2}n$，

線段樹中查詢/修改的複雜度為$\log _{2}n$

那麼總的複雜度就是$\left( \log _{2}n\right) ^{2}$

例題

洛谷P3379 【模板】最近公共祖先（LCA）

樹剖可以求LCA，沒想到吧

http://www.cnblogs.com/zwfymqz/p/8097366.html

洛谷P2590 [ZJOI2008]樹的統計

http://www.cnblogs.com/zwfymqz/p/7157156.html

這份代碼是以前寫的，可能比較醜，下麵兩份是剛剛寫的

洛谷P3178 [HAOI2015]樹上操作

http://www.cnblogs.com/zwfymqz/p/8094286.html

洛谷P3038 [USACO11DEC]牧草種植Grass Planting

有點意思

http://www.cnblogs.com/zwfymqz/p/8094429.html


您的分享是我們最大的動力!

-Advertisement-
Play Games
更多相關文章
  • Vue（SPA） WebPack模塊化打包、SEO優化、全瀏覽器相容完整解決方案
    白駒過隙，時光荏苒 大概去年這個時候寫了angular 結合webpack的一套前端方案，今年此時祭出vue2結合webpack2的一套前端方案。 明年的這個時候我又是在做什麼... 讀在最前面： 1、本文講述Vue，Webpack 模塊化、SEO優化、全瀏覽器相容（ie8以上）、圖片輪播等案例方案 ...
  • 細談最近上線的Vue2.0項目（一）
    8月初離職，來到現在的新東家負責一個新的項目。而我最近開發的兩個webapp一直都是以Vue為主，這也是這篇文章的由來。 正文前的胡侃&一點點吐槽 在經歷了兩個公司不同的項目後，發現都存在一個很致命卻又如此相似的問題。就是領導層的決策，導致項目的開發後期加班嚴重。領導們普遍都是先DIY，然後等到項目 ...
  • 在CesiumVR基礎上實現3D左右立體視覺
    整體思路 代碼部分 2.對左屏（相機偏移的場景）重新進行渲染（暫時解決方案，對相機外的場景同樣進行渲染,存在的問題：效率太低） 有待解決的問題 相機偏移後（左屏），應當對場景（左屏）重新進行渲染。具體指 ...
  • 關於background和backgroundColor
    for(var i=0;i<as.length;i++){ as[i].onmouseover=function(){this.style.backgroundColor='grey';} as[i].onmouseout=function(){this.style.backgroundColor= ...
  • 蘋果安卓移動端當前頁面刷新一次
    <script>window.onload = function(){ var u = navigator.userAgent; var isiOS = !!u.match(/\(i[^;]+;( U;)? CPU.+Mac OS X/); if(isiOS){ if(location.search ...
  • Spring（mvc）思維導圖
    spring mvc簡介與運行原理 Spring的模型-視圖-控制器（MVC）框架是圍繞一個DispatcherServlet來設計的，這個Servlet會把請求分發給各個處理器，並支持可配置的處理器映射、視圖渲染、本地化、時區與主題渲染等，甚至還能支持文件上傳。 原理.png (1) Http請求 ...
  • 洛谷P3379 【模板】最近公共祖先（LCA）（樹鏈剖分）
    題目描述 如題，給定一棵有根多叉樹，請求出指定兩個點直接最近的公共祖先。 輸入輸出格式 輸入格式： 第一行包含三個正整數N、M、S，分別表示樹的結點個數、詢問的個數和樹根結點的序號。 接下來N-1行每行包含兩個正整數x、y，表示x結點和y結點之間有一條直接連接的邊（數據保證可以構成樹）。 接下來M行 ...
  • 1507: [NOI2003]Editor（塊狀鏈表）
    1507: [NOI2003]Editor Description Input 輸入文件editor.in的第一行是指令條數t，以下是需要執行的t個操作。其中： 為了使輸入文件便於閱讀，Insert操作的字元串中可能會插入一些回車符，請忽略掉它們（如果難以理解這句話，可以參考樣例）。 除了回車符之外 ...
一周排行
    -Advertisement-
    Play Games
  • 移動開發（一）：使用.NET MAUI開發第一個安卓APP
    移動開發（一）：使用.NET MAUI開發第一個安卓APP 對於工作多年的C#程式員來說，近來想嘗試開發一款安卓APP，考慮了很久最終選擇使用.NET MAUI這個微軟官方的框架來嘗試體驗開發安卓APP，畢竟是使用Visual Studio開發工具，使用起來也比較的順手，結合微軟官方的教程進行了安卓 ...
  • wpf ToggleButton選中效果和一個登錄界面
    前言 QuestPDF 是一個開源 .NET 庫，用於生成 PDF 文檔。使用了C# Fluent API方式可簡化開發、減少錯誤並提高工作效率。利用它可以輕鬆生成 PDF 報告、發票、導出文件等。 項目介紹 QuestPDF 是一個革命性的開源 .NET 庫，它徹底改變了我們生成 PDF 文檔的方 ...
  • 彈幕樹洞項目功能新增篇
    項目地址 項目後端地址： https://github.com/ZyPLJ/ZYTteeHole 項目前端頁面地址： ZyPLJ/TreeHoleVue (github.com) https://github.com/ZyPLJ/TreeHoleVue 目前項目測試訪問地址： http://tree ...
  • 第27篇 sqlserver2022詳細安裝步驟
    話不多說，直接開乾 一.下載 1.官方鏈接下載： https://www.microsoft.com/zh-cn/sql-server/sql-server-downloads 2.在下載目錄中找到下麵這個小的安裝包 SQL2022-SSEI-Dev.exe，運行開始下載SQL server； 二. ...
  • .NET 開源高性能 MQTT 類庫
    前言 隨著物聯網（IoT）技術的迅猛發展，MQTT（消息隊列遙測傳輸）協議憑藉其輕量級和高效性，已成為眾多物聯網應用的首選通信標準。 MQTTnet 作為一個高性能的 .NET 開源庫，為 .NET 平臺上的 MQTT 客戶端與伺服器開發提供了強大的支持。 本文將全面介紹 MQTTnet 的核心功能 ...
  • Serilog文檔翻譯系列（六） - 可用的接收器、增強器、格式化輸出
    Serilog支持多種接收器用於日誌存儲，增強器用於添加屬性，LogContext管理動態屬性，支持多種輸出格式包括純文本、JSON及ExpressionTemplate。還提供了自定義格式化選項，適用於不同需求。 ...
  • 警惕 Visual Studio 屬性求值副作用導致邏輯不符合預期
    目錄簡介獲取 HTML 文檔解析 HTML 文檔測試參考文章 簡介 動態內容網站使用 JavaScript 腳本動態檢索和渲染數據，爬取信息時需要模擬瀏覽器行為，否則獲取到的源碼基本是空的。 本文使用的爬取步驟如下： 使用 Selenium 獲取渲染後的 HTML 文檔 使用 HtmlAgility ...
  • [使用目前最新版]HybridCLR6.9.0+YooAsset2.2.4實現純C# Unity熱更新方案 (一)
    1.前言 什麼是熱更新 游戲或者軟體更新時，無需重新下載客戶端進行安裝，而是在應用程式啟動的情況下，在內部進行資源或者代碼更新 Unity目前常用熱更新解決方案 HybridCLR，Xlua，ILRuntime等 Unity目前常用資源管理解決方案 AssetBundles，Addressable， ...
  • 在 ASP.NET Core Web API 中使用操作篩選器統一處理通用操作
    本文章主要是在C# ASP.NET Core Web API框架實現向手機發送驗證碼簡訊功能。這裡我選擇是一個互億無線簡訊驗證碼平臺，其實像阿裡雲，騰訊雲上面也可以。 首先我們先去 互億無線 https://www.ihuyi.com/api/sms.html 去註冊一個賬號 註冊完成賬號後，它會送 ...
  • 第28篇 如何.net中實現高效可靠數據同步api
    通過以下方式可以高效，並保證數據同步的可靠性 1.API設計 使用RESTful設計，確保API端點明確，並使用適當的HTTP方法（如POST用於創建，PUT用於更新）。 設計清晰的請求和響應模型，以確保客戶端能夠理解預期格式。 2.數據驗證 在伺服器端進行嚴格的數據驗證，確保接收到的數據符合預期格 ...
所有分類