最短路徑之迪傑斯特拉（Dijkstra）演算法

迪傑斯特拉（Dijkstra）演算法主要是針對沒有負值的有向圖，求解其中的單一起點到其他頂點的最短路徑演算法。本文主要總結迪傑斯特拉（Dijkstra）演算法的原理和演算法流程，最後通過程式實現在一個帶權值的有向圖中，選定某一個起點，求解到達其它節點的最短路徑，來加深對演算法的理解。

1 演算法原理

迪傑斯特拉（Dijkstra）演算法是一個按照路徑長度遞增的次序產生的最短路徑演算法。下圖為帶權值的有向圖，作為程式中的實驗數據。

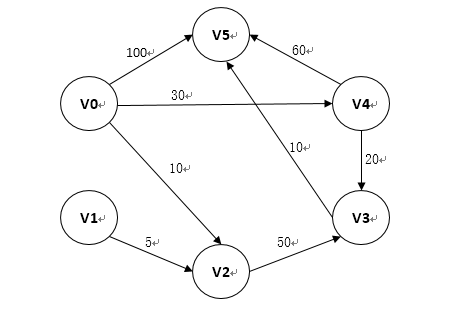
其中，帶權值的有向圖採用鄰接矩陣graph來進行存儲，在計算中就是採用n*n的二維數組來進行存儲，v0-v5表示數組的索引編號0-5，二維數組的值表示節點之間的權值，若兩個節點不能通行，比如，v0->v1不能通行，那麼$graph[0,1]=\infty$ （採用電腦中最大正整數來進行表示）。那如何求解從v0每個v節點的最短路徑長度呢?

首先，引進一個輔助數組cost，它的每個值$cost[i]$表示當前所找到的從起始點v0到終點vi的最短路徑的權值（長度花費），該數組的初態為：若從v0到vi有弧，則$cost[i]$為弧上的權值，否則置$cost[i]$為$\infty$ 。顯然，長度為：
$$
cost[j]=Min_i(graph[0,i] | v_i \in V)
$$
的路徑就是從v0出發的長度最短的一條最短路徑。此路徑為$(v_0,v_j)$ ，那麼下次長度次短的路徑必定是弧$(v_0,v_i)$ 上的權值$cost[i](v_i \in V)$，或者是$cost[k](v_k \in S)$ 和弧$(v_k,v_i)$ 的權值之和。其中V：待求解最短路徑的節點j集合；S：已求解最短路徑的節點集合。

其實迪傑斯特拉（Dijkstra）最短路徑演算法是上一篇文迷宮問題求解之“A*搜索”（二）所講到的 A*搜索演算法中的一個特例，當A *搜索演算法中 h(n)函數為0的時候，那麼它就是迪傑斯特拉演算法，演算法原理一樣，只不過在寫程式的時候稍微有點區別而已。

2 演算法流程

根據上面的演算法原理分析，下麵描述演算法的實現流程。

1. 初始化：初始化輔助數組cost，從v0出發到圖上其餘節點v的初始權值為：$cost[i]=graph[0,i] \ |\ v_i \in V$ ；初始化待求節點S集合，它的初始狀態為空集。

2. 選擇節點$v_j$ ，使得$cost[j]=Min ( cost[i] | v_i \in V -S )$ ，$v_j$ 就是當前求的一條從v0出發的最短路徑的終點，修改S集合，使得$S=S\bigcup V_j$ 。

3. 修改從v0出發到節點V-S上任一頂點$v_k$ 可達的最短路徑，若cost[j]+graph[j,k]<cost[k] ，則修改cost[k]為：cost[k]=cost[j]+graph[j,k] 。

4. 重覆操作2，3步驟，直到求解集合V中的所有節點為止。

其中最短路徑的存儲採用一個path整數數組，path[i]的值記錄vi的前一個節點的索引，通過path一直追溯到起點，就可以找到從vi到起始節點的最短路徑。比如起始節點索引為0，若path[3]=4, path[4]=0；那麼節點v2的最短路徑為，v0->v4->v3。

3 演算法實現

採用c#語言對第2節中的演算法流程進行實現，關鍵代碼如下。

3.1 最短路徑代碼

class DijkstraSolution
{
    /*
        * 求解各節點最短路徑，獲取path，和cost數組，
        * path[i]表示vi節點的前繼節點索引，一直追溯到起點。
        * cost[i]表示vi節點的花費
        */
    public static void FindShortestPath(int[,] graph,int startIndex, int[] path, int[] cost,int max)
    {
        int nodeCount = graph.GetLength(0);
        bool[] v = new bool[nodeCount];
        //初始化 path，cost，V
        for (int i = 0; i <nodeCount ; i++)
        {
            if (i == startIndex)//如果是出發點
            {
                v[i] = true;//
            }
            else
            {
                cost[i] = graph[startIndex,i ];
                if (cost[i] < max) path[i] = startIndex;
                else path[i] = -1;
                v[i] = false;
            }
        }
        //
        for(int i=1;i<nodeCount;i++)//求解nodeCount-1個
        {
            int minCost = max ;
            int curNode=-1;
            for (int w = 0; w < nodeCount; w++)
            {
                if (!v[w])//未在V集合中
                { 
                    if(cost[w]<minCost)
                    {
                        minCost = cost[w];
                        curNode = w;
                    }
                }
            }//for  獲取最小權值的節點
            if (curNode == -1) break;//剩下都是不可通行的節點，跳出迴圈
            v[curNode] = true;
            for (int w = 0; w < nodeCount; w++)
            {
                if (!v[w] && (graph[curNode, w] + cost[curNode] < cost[w]))
                {
                    cost[w] = graph[curNode, w] + cost[curNode];//更新權值
                    path[w] = curNode;//更新路徑
                }
            }//for 更新其他節點的權值（距離）和路徑
        }//
    }
}

3.2 調用代碼

int max = 10000;
int[,] graph = new int[6, 6] {
    {max,max,10,max,30,100},
    {max,max,5,max,max,max},
    {max,max,max,50,max,max},
    {max,max,max,max,max,10},
    {max,max,max,20,max,60},
    {max,max,max,max,max,max},
};
int []path = new int[6];
int []cost = new int[6];
DijkstraSolution.FindShortestPath(graph, 0, path, cost,max);

3.3 運行結果

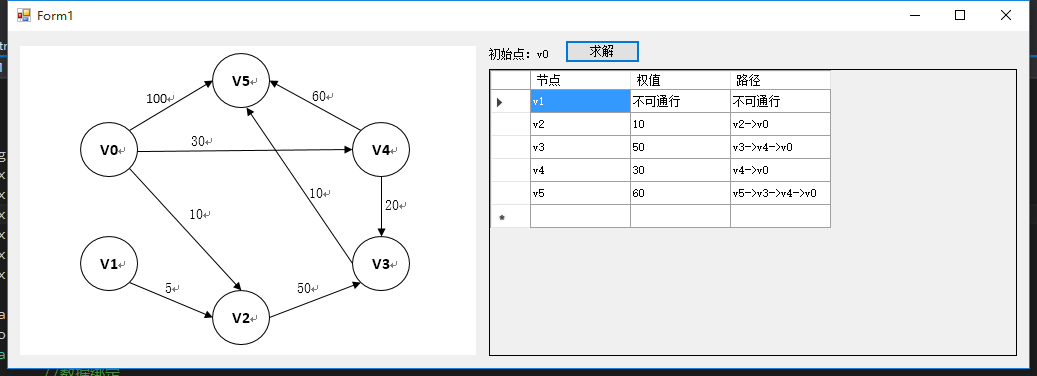
4 總結

迪傑特拉斯演算法求解了一個起始節點到所有其他節點的最短路徑，時間複雜度為$O(n^2)$ ，即使人們可能只想知道從起始節點到某個特定的節點的最短路徑，時間複雜度同樣為$O(n^2)$ 。

理解一個演算法和實現一個演算法還有有些區別的。理解一個演算法，只需要明白演算法原理和它的邏輯過程即可，但是實現一個演算法，不僅要明白演算法的邏輯過程，還考究我們的程式設計能力。

5 參考資料和資源

參考資料：嚴蔚敏的《數據結構c語言版》

源代碼：http://download.csdn.net/download/mingge38/9657216