某大廠面試題1 1. 分散式事務的一致性問題 事務的四大特性(ACID) 原子性(Atomicity):一個事務(transaction)要麼沒有開始,要麼全部完成,不存在中間狀態。 一致性(Consistency):事務的執行不會破壞數據的正確性,即符合約束。 隔離性(Isolation):多個事 ...
某大廠面試題1
1. 分散式事務的一致性問題
事務的四大特性(ACID)
原子性(Atomicity):一個事務(transaction)要麼沒有開始,要麼全部完成,不存在中間狀態。
一致性(Consistency):事務的執行不會破壞數據的正確性,即符合約束。
隔離性(Isolation):多個事務不會相互破壞。
持久性(Durability):事務一旦提交成功,對數據的修改不會丟失。
其中原子性、持久性、隔離性都是為了保證一致性的。
事務型資料庫必須要解決的問題是數據的一致性問題。這裡的一致性指的是ACID中的C,如果不滿足C,會有多種數據異常,如臟讀、不可重覆讀、幻讀、讀偏序、寫偏序等數據異常。隔離性這一特性的出現就是為瞭解決一類由於併發事務而導致的數據不一致問題。
舉例:
用戶通過手機支付購買商家的商品,在支付過程中需要在一系列的系統進行處理:支付系統中需要創建支付單,在賬務系統進行用戶餘額扣減,隨後通知上游系統完成支付。在這個支付過程中,三種系統之間需要嚴格保證一致性。不能出現支付單成功但是餘額沒扣,也不能出現餘額扣除後商家不發貨的情況。
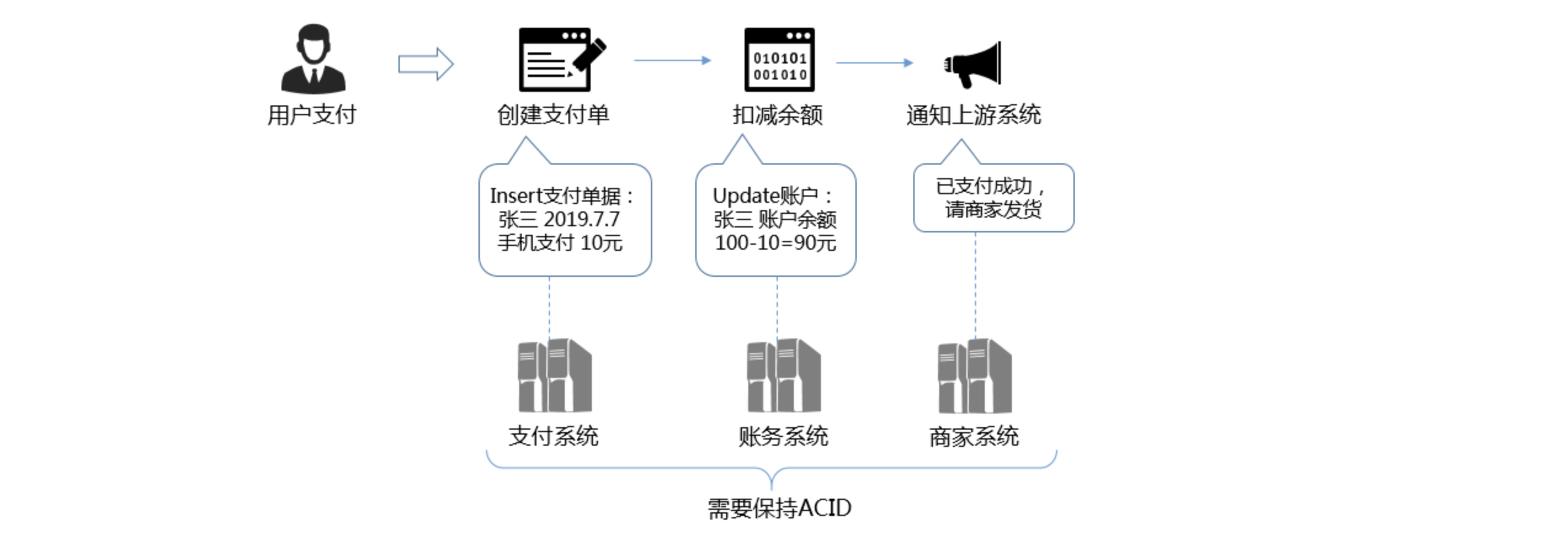
分散式系統屬於非同步系統(Asynchronous system model):不同進程的處理器速度可能差別很大,時鐘偏移可能很大,消息傳播延遲可能很大(可能很大意味著沒有最大值限制)。這樣就帶來一個很大的問題:超時。超時一定有可能發生,但是超時又無法判斷究竟是成功還是失敗了,導致整個業務狀態異常。而單台電腦屬於同步系統(Synchronous system model),即使不同進程的處理器速度差異、時鐘偏移延遲、消息延遲都有最大值的。
CAP理論
一個分散式系統最多只能同時滿足一致性(Consistency)、可用性(Availability)和分區容錯性(Partition tolerance)這三項中的兩項。
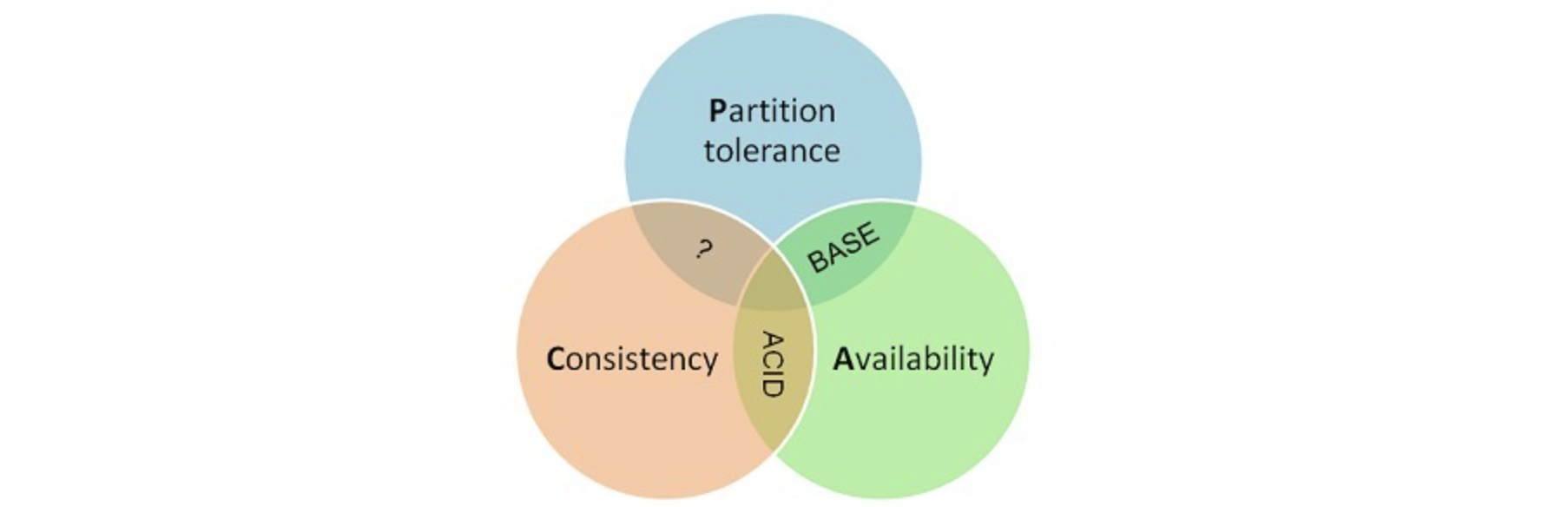
- Consistency 一致性:每次讀取獲得的都是最新寫入的數據,即寫操作之後的讀操作,必須返回該值
- Availability 可用性:服務在正常響應時間內一直可用,返回的狀態都是成功
- Partition-tolerance 分區容錯性:即使遇到某節點或網路故障的時候,系統仍能夠正常提供服務
儘管CAP狹義上針對的是分散式存儲系統,但它一樣可以應用於普遍的分散式系統。由於分區容錯性(P)是分散式系統最重要的特點,因此CAP可以理解為:當網路發生分區(P)時,要麼選擇C一致性,要麼選擇A可用性。
舉例來說,具體到上文描述的用戶支付的例子中,當網路存在異常時,要麼用戶可能暫時無法支付,要麼用戶的餘額可能不會立刻扣減。這兩種選擇就是在架構設計中對可用性和一致性的權衡。
2. 堆排序
堆排序(Heapsort)是指利用堆這種數據結構所設計的一種排序演算法。堆積是一個近似完全二叉樹的結構,並同時滿足堆積的性質:即子結點的鍵值或索引總是小於(或者大於)它的父節點。堆排序可以說是一種利用堆的概念來排序的選擇排序。複雜度是O(nlogn)
堆排序是利用堆這種數據結構所設計的一種排序演算法。堆實際上是一個完全二叉樹結構。問:那麼什麼是完全二叉樹呢?答:假設一個二叉樹的深度為h,除第 h 層外,其它各層 (1~h-1) 的結點數都達到最大個數,第 h 層所有的結點都連續集中在最左邊,這就是完全二叉樹。

小頂堆滿足: Key[i] <= key[2i+1] && Key[i] <= key[2i+2]
大頂堆滿足: Key[i] >= Key[2i+1] && key >= key[2i+2]每個結點的值都大於或等於其左右孩子的值
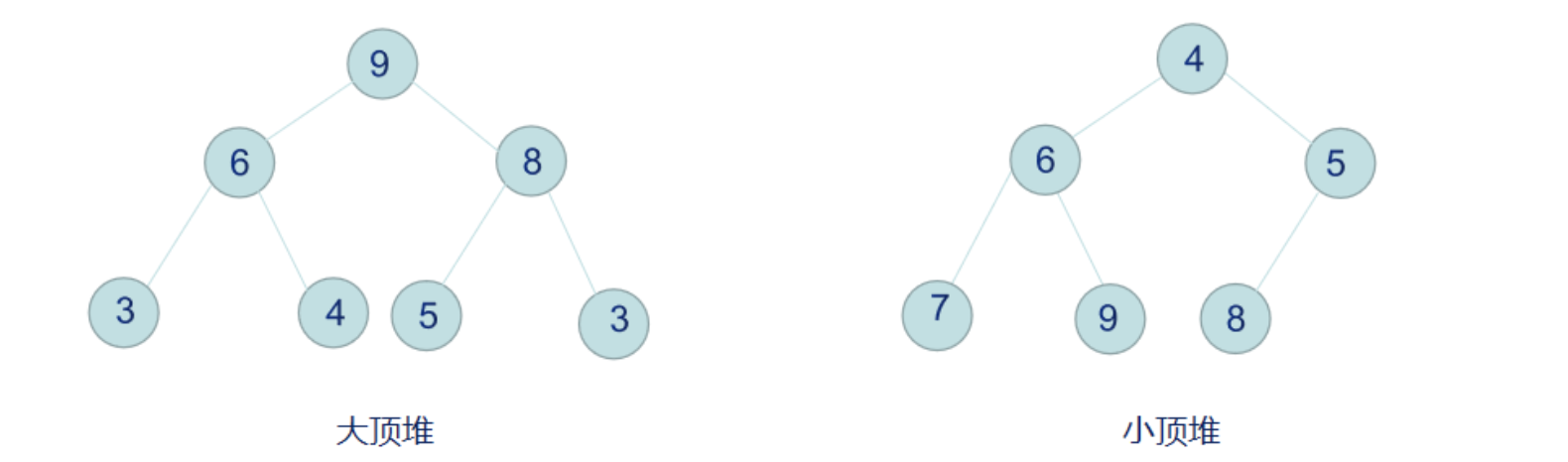
步驟
- 將待排序的數組初始化為大頂堆,該過程即建堆。
- 將堆頂元素與最後一個元素進行交換,除去最後一個元素外可以組建為一個新的大頂堆。
- 由於第二步堆頂元素跟最後一個元素交換後,新建立的堆不是大頂堆,需要重新建立大頂堆。重覆上面的處理流程,直到堆中僅剩下一個元素。
假設我們有一個待排序的數組 arr = [4, 6, 7, 2, 9, 8, 3, 5], 我們把這個數組構造成為一個二叉樹,如下圖:
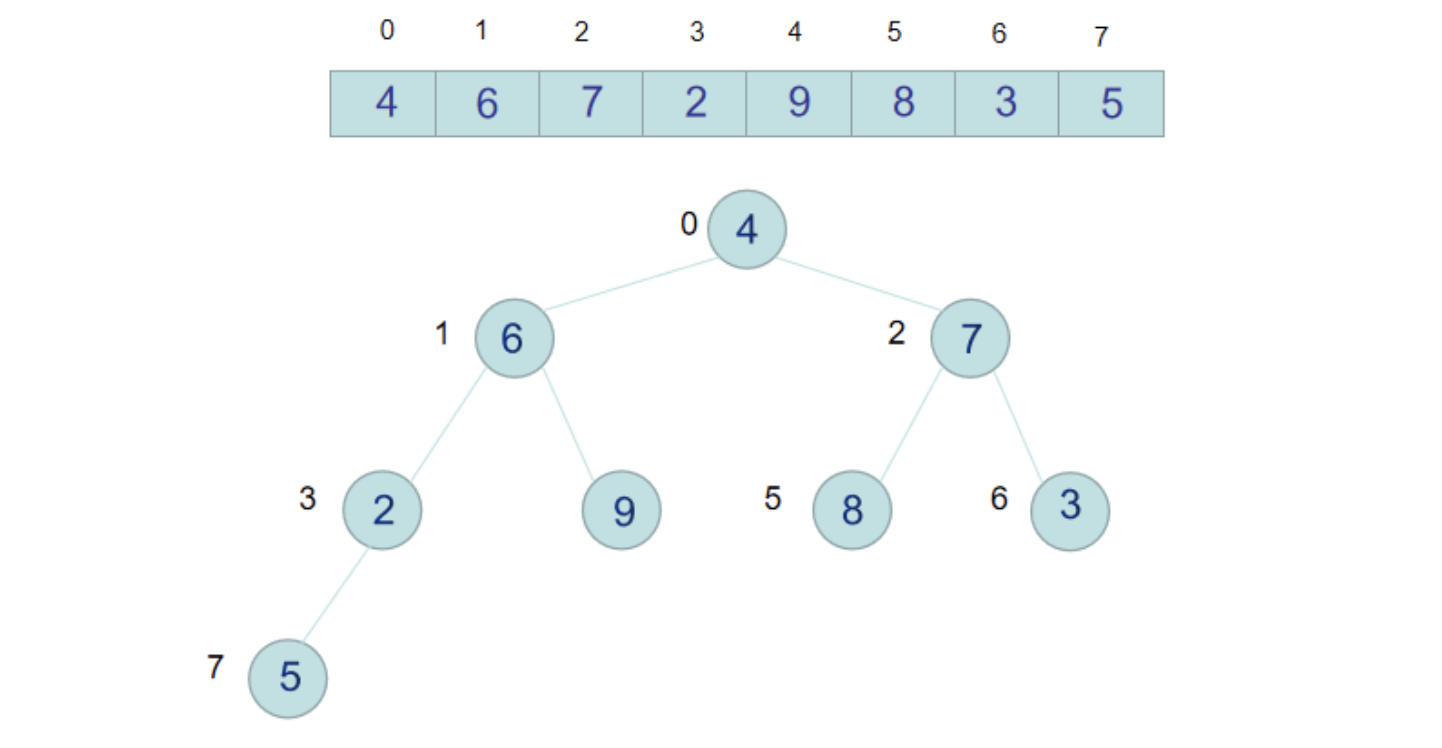
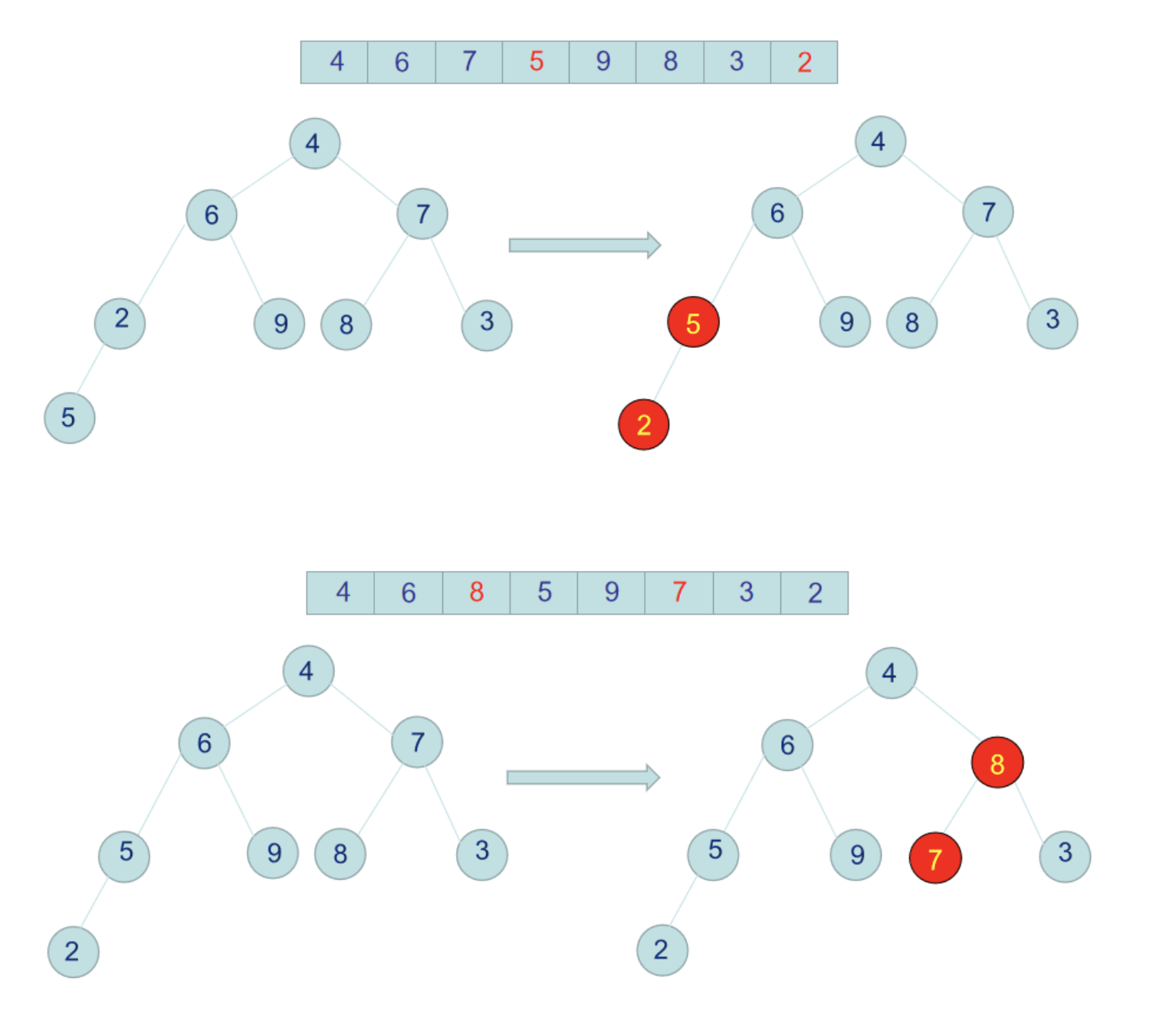
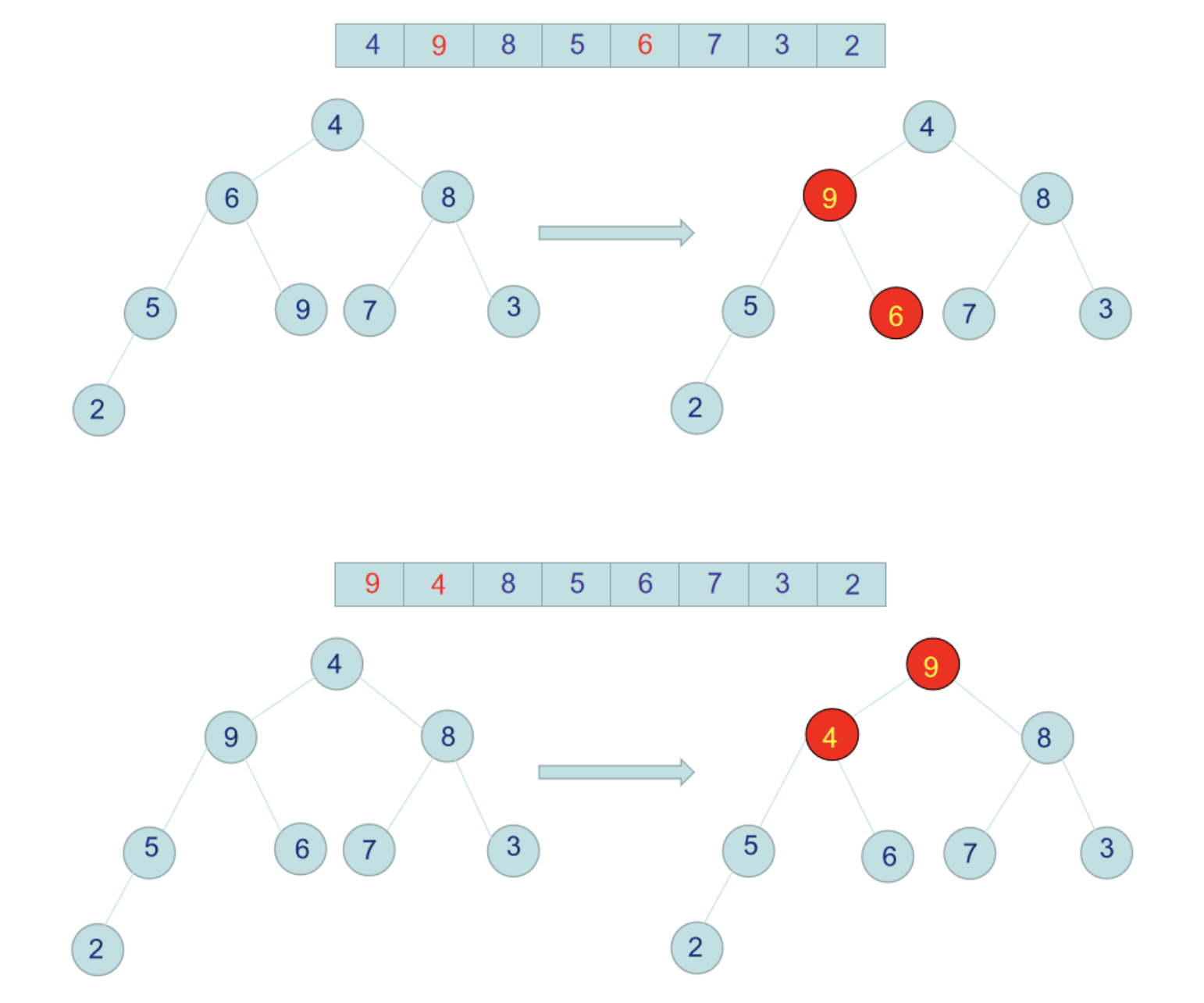
此時9跟4交換後,4這個節點下麵的樹就不是不符合大頂堆了,所以要針對4這個節點跟它的左右節點再次比較,置換成較大的值,4跟左右子節點比較後,應該跟6交換位置。
那麼至此,整個二叉樹就是一個完完整整的大頂堆了,每個節點都不小於左右子節點。此時我們把堆的跟節點,即數組最大值9跟數組最後一個元素2交換位置,那麼9就是排好序的放在了數組最後一個位置。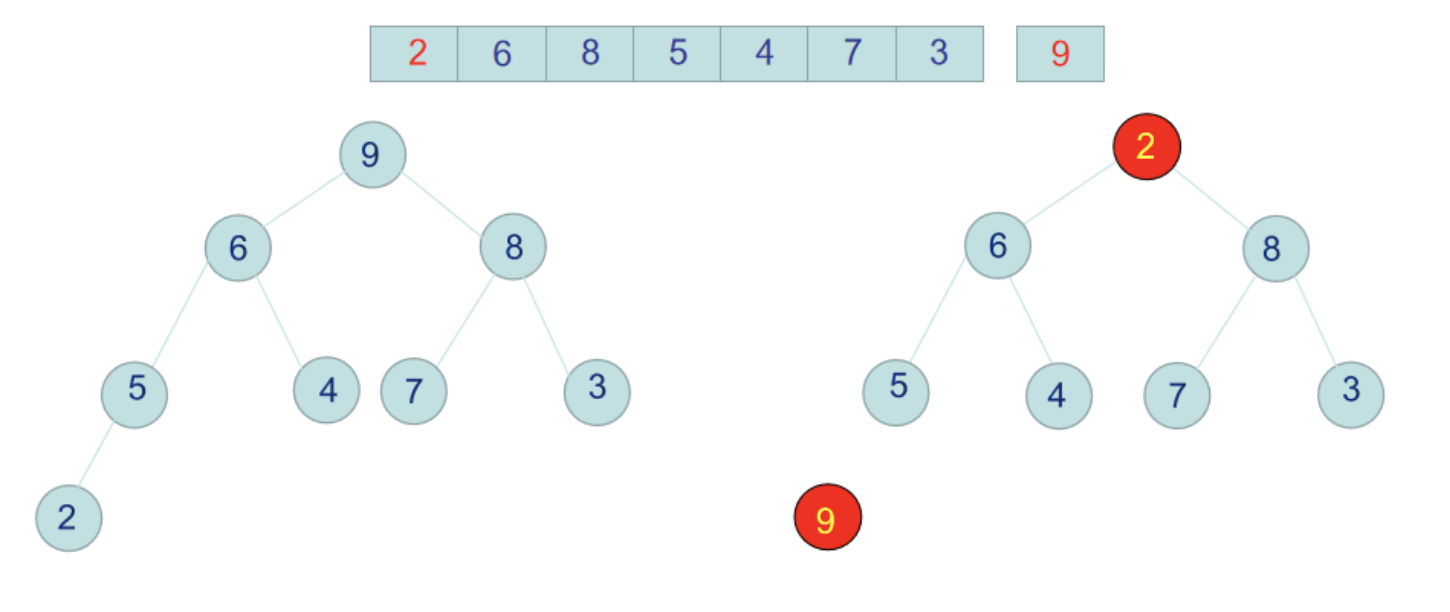
2到了跟節點後,新的堆不滿足大頂堆,我們需要重覆上面的步驟,重新構造大頂堆,然後把大頂堆根節點放到二叉樹後面作為排好序的數組放好。就這樣利用大頂堆一個一個的數字排好序。
值得註意的一個地方是,上面我們把9和2交換位置後,2處於二叉樹根節點,2需要跟右子樹8交換位置,交換完位置後,右子樹需要重新遞歸調整大頂堆,但是左子樹6這邊,已經是滿足大頂堆屬性,因為不需要再操作。
class Solution(object):
def heap_sort(self, nums):
i, l = 0, len(nums)
self.nums = nums
# 構造大頂堆,從非葉子節點開始倒序遍歷,因此是l//2 -1 就是最後一個非葉子節點
for i in range(l // 2 - 1, -1, -1):
self.build_heap(i, l - 1)
# 上面的迴圈完成了大頂堆的構造,那麼就開始把根節點跟末尾節點交換,然後重新調整大頂堆
for j in range(l - 1, -1, -1):
nums[0], nums[j] = nums[j], nums[0]
self.build_heap(0, j - 1)
print("第{}輪堆排序:{}".format(l - j, nums))
return nums
def build_heap(self, i, l):
"""構建大頂堆"""
nums = self.nums
left, right = 2 * i + 1, 2 * i + 2 ## 左右子節點的下標
large_index = i
if left <= l and nums[i] < nums[left]:
large_index = left
if right <= l and nums[left] < nums[right]:
large_index = right
# 通過上面跟左右節點比較後,得出三個元素之間較大的下標,如果較大下表不是父節點的下標,說明交換後需要重新調整大頂堆
if large_index != i:
nums[i], nums[large_index] = nums[large_index], nums[i]
self.build_heap(large_index, l)
s = Solution()
li = [4, 6, 7, 2, 9, 8, 3, 5]
s.heap_sort(li)
第1輪堆排序:[8, 6, 7, 5, 4, 2, 3, 9]
第2輪堆排序:[7, 6, 3, 5, 4, 2, 8, 9]
第3輪堆排序:[6, 5, 3, 2, 4, 7, 8, 9]
第4輪堆排序:[5, 4, 3, 2, 6, 7, 8, 9]
第5輪堆排序:[4, 2, 3, 5, 6, 7, 8, 9]
第6輪堆排序:[3, 2, 4, 5, 6, 7, 8, 9]
第7輪堆排序:[2, 3, 4, 5, 6, 7, 8, 9]
3. 快速排序
快速排序是一種非常高效的排序演算法,採用 “分而治之” 的思想,把大的拆分為小的,小的拆分為更小的。其原理是,對於給定的記錄,選擇一個基準數,通過一趟排序後,將原序列分為兩部分,使得前面的比後面的小,然後再依次對前後進行拆分進行快速排序,遞歸該過程,直到序列中所有記錄均有序。
首先取序列第一個元素為基準元素pivot=R[low]。i=low,j=high。 2:從後向前掃描,找小於等於pivot的數,如果找到,R[i]與R[j]交換,i++。 3:從前往後掃描,找大於pivot的數,如果找到,R[i]與R[j]交換,j--。 4:重覆2~3,直到i=j,返回該位置mid=i,該位置正好為pivot元素。 完成一趟排序後,以mid為界,將序列分為兩部分,左序列都比pivot小,有序列都比pivot大,然後再分別對這兩個子序列進行快速排序。
以序列(30,24,5,58,16,36,12,42,39)為例,進行演示:
1、初始化,i=low,j=high,pivot=R[low]=30:
| i | j | |||||||
|---|---|---|---|---|---|---|---|---|
| 30 | 24 | 5 | 58 | 16 | 26 | 12 | 41 | 39 |
2、從後往前找小於等於pivot的數,找到R[j]=12
| i | j | |||||||
|---|---|---|---|---|---|---|---|---|
| 30 | 24 | 5 | 58 | 16 | 26 | 12 | 41 | 39 |
- R[i]與R[j]交換,i++
| i | j | |||||||
|---|---|---|---|---|---|---|---|---|
| 12 | 24 | 5 | 58 | 16 | 26 | 30 | 41 | 39 |
3、從前往後找大於pivot的數,找到R[i]=58
| i | j | |||||||
|---|---|---|---|---|---|---|---|---|
| 12 | 24 | 5 | 58 | 16 | 26 | 30 | 41 | 39 |
- R[i]與R[j]交換,j--
| i | j | |||||||
|---|---|---|---|---|---|---|---|---|
| 12 | 24 | 5 | 30 | 16 | 26 | 58 | 41 | 39 |
4、從後往前找小於等於pivot的數,找到R[j]=16
| i | j | |||||||
|---|---|---|---|---|---|---|---|---|
| 12 | 24 | 5 | 30 | 16 | 26 | 58 | 41 | 39 |
- R[i]與R[j]交換,i++
| i,j | ||||||||
|---|---|---|---|---|---|---|---|---|
| 12 | 24 | 5 | 16 | 30 | 26 | 58 | 41 | 39 |
5、從前往後找大於pivot的數,這時i=j,第一輪排序結束,返回i的位置,mid=i
| Low | mid-1 | mid | mid+1 | High | ||||
|---|---|---|---|---|---|---|---|---|
| 12 | 24 | 5 | 16 | 30 | 26 | 58 | 41 | 3 |
此時已mid為界,將原序列一分為二,左子序列為(12,24,5,18)元素都比pivot小,右子序列為(36,58,42,39)元素都比pivot大。然後在分別對兩個子序列進行快速排序,最後即可得到排序後的結果。
def quick_sort(lists,i,j):
if i >= j:
return list
pivot = lists[i]
low = i
high = j
while i < j:
while i < j and lists[j] >= pivot:
j -= 1
lists[i]=lists[j]
while i < j and lists[i] <=pivot:
i += 1
lists[j]=lists[i]
lists[j] = pivot
quick_sort(lists,low,i-1)
quick_sort(lists,i+1,high)
return lists
if __name__=="__main__":
lists=[30,24,5,58,18,36,12,42,39]
print("排序前的序列為:")
for i in lists:
print(i,end =" ")
print("\n排序後的序列為:")
for i in quick_sort(lists,0,len(lists)-1):
print(i,end=" ")
4. 進程間通信的方法
進程和線程
進程是對運行時程式的封裝,是系統進行資源調度和分配的基本單位,實現了操作系統的併發;
線程是進程的子任務,是CPU調度和分派的基本單位,用於保證程式的實時性,實現進程內部的併發;線程是操作系統可識別的最小執行和調度單位。每個線程都獨自占用一個虛擬處理器:獨自的寄存器組,指令計數器和處理器狀態。每個線程完成不同的任務,但是共用同一地址空間(也就是同樣的動態記憶體,映射文件,目標代碼等等),打開的文件隊列和其他內核資源。
區別:
- 一個線程只能屬於一個進程,而一個進程可以有多個線程,但至少有一個線程。線程依賴於進程而存在。
- 進程在執行過程中擁有獨立的記憶體單元,而多個線程共用進程的記憶體。(資源分配給進程,同一進程的所有線程共用該進程的所有資源。同一進程中的多個線程共用代碼段(代碼和常量),數據段(全局變數和靜態變數),擴展段(堆存儲)。但是每個線程擁有自己的棧段,棧段又叫運行時段,用來存放所有局部變數和臨時變數。)
- 進程是資源分配的最小單位,線程是CPU調度的最小單位;
- 系統開銷: 由於在創建或撤消進程時,系統都要為之分配或回收資源,如記憶體空間、I/o設備等。因此,操作系統所付出的開銷將顯著地大於在創建或撤消線程時的開銷。類似地,在進行進程切換時,涉及到整個當前進程CPU環境的保存以及新被調度運行的進程的CPU環境的設置。而線程切換隻須保存和設置少量寄存器的內容,並不涉及存儲器管理方面的操作。可見,進程切換的開銷也遠大於線程切換的開銷。
- 通信:由於同一進程中的多個線程具有相同的地址空間,致使它們之間的同步和通信的實現,也變得比較容易。進程間通信IPC,線程間可以直接讀寫進程數據段(如全局變數)來進行通信——需要進程同步和互斥手段的輔助,以保證數據的一致性。在有的系統中,線程的切換、同步和通信都無須操作系統內核的干預
- 進程編程調試簡單可靠性高,但是創建銷毀開銷大;線程正相反,開銷小,切換速度快,但是編程調試相對複雜。
- 進程間不會相互影響 ;線程一個線程掛掉將導致整個進程掛掉
- 進程適應於多核、多機分佈;線程適用於多核
進程間通信的方式有:1、無名管道( pipe );2、高級管道(popen);3、有名管道 (named pipe);4、消息隊列( message queue );5、信號量( semophore );7、共用記憶體( shared memory );8、套接字( socket )。
1 、無名管道 ( pipe ) :
管道是一種半雙工的通信方式,數據只能單向流動,而且只能在具有親緣關係的進程間使用。進程的親緣關係通常是指父子進程關係。
2 、高級管道 (popen) :
將另一個程式當做一個新的進程在當前程式進程中啟動,則它算是當前程式的子進程,這種方式我們成為高級管道方式。
3 、有名管道 (named pipe) :
有名管道也是半雙工的通信方式,但是它允許無親緣關係進程間的通信。
4 、消息隊列 ( message queue ) :
消息隊列是由消息的鏈表,存放在內核中並由消息隊列標識符標識。消息隊列剋服了信號傳遞信息少、管道只能承載無格式位元組流以及緩衝區大小受限等缺點。
5 、信號量 ( semophore ) :
信號量是一個計數器,可以用來控制多個進程對共用資源的訪問。它常作為一種鎖機制,防止某進程正在訪問共用資源時,其他進程也訪問該資源。因此,主要作為進程間以及同一進程內不同線程之間的同步手段。
6 、信號 ( sinal ) :
信號是一種比較複雜的通信方式,用於通知接收進程某個事件已經發生。
7 、共用記憶體 ( shared memory ) :
共用記憶體就是映射一段能被其他進程所訪問的記憶體,這段共用記憶體由一個進程創建,但多個進程都可以訪問。共用記憶體是最快的 IPC 方式,它是針對其他進程間通信方式運行效率低而專門設計的。它往往與其他通信機制,如信號兩,配合使用,來實現進程間的同步和通信。
8 、套接字 ( socket ) :
套解口也是一種進程間通信機制,與其他通信機制不同的是,它可用於不同機器間的進程通信。
為什麼要進程間通信
由於每個進程都是相對獨立運行的,且每個用戶請求都可能導致多個進程在操作系統中運行,如果多個進程之間需要協作完成任務,那麼進程間可能就需要進行相互通信獲取數據,這種通信方式就稱作為進程間通信(Inter-process communication IPC)。
5. 操作系統記憶體回收機制
記憶體回收指的是對用戶空間中的堆段和文件映射段進行回收(用戶使用 malloc、mmap 等分配出去的空間)。用戶可以手動地使用 free()等進行記憶體釋放。當沒有空閑的物理記憶體時,內核就會開始自動地進行回收記憶體工作。回收的方式主要是兩種:後臺記憶體回收和直接記憶體回收。
- 後臺記憶體回收(kswapd):在物理記憶體緊張的時候,會喚醒 kswapd 內核線程來回收記憶體,這個回收記憶體的過程非同步的,不會阻塞進程的執行。
- 直接記憶體回收(direct reclaim):如果後臺非同步回收跟不上進程記憶體申請的速度,就會開始直接回收,這個回收記憶體的過程是同步的,會阻塞進程的執行。
如果直接記憶體回收後,空閑的物理記憶體仍然無法滿足此次物理記憶體的申請,那麼內核就會觸發 OOM (Out of Memory)機制,根據演算法選擇一個占用物理記憶體較高的進程,然後將其殺死,釋放記憶體資源,直到釋放足夠的記憶體。
本文來自博客園,作者:ivanlee717,轉載請註明原文鏈接:https://www.cnblogs.com/ivanlee717/p/17267314.html



