漢諾塔問題分治求解

漢諾塔問題

在經典漢諾塔問題中，有 3 根柱子及 n 個不同大小的穿孔圓盤，盤子可以滑入任意一根柱子。一開始，所有盤子自上而下按升序依次套在第一根柱子上(即每一個盤子只能放在更大的盤子上面)。移動圓盤時受到以下限制:
(1) 每次只能移動一個盤子;
(2) 盤子只能從柱子頂端滑出移到下一根柱子;
(3) 盤子只能疊在比它大的盤子上。

請編寫程式，用棧將所有盤子從第一根柱子移到最後一根柱子。

你需要原地修改棧。

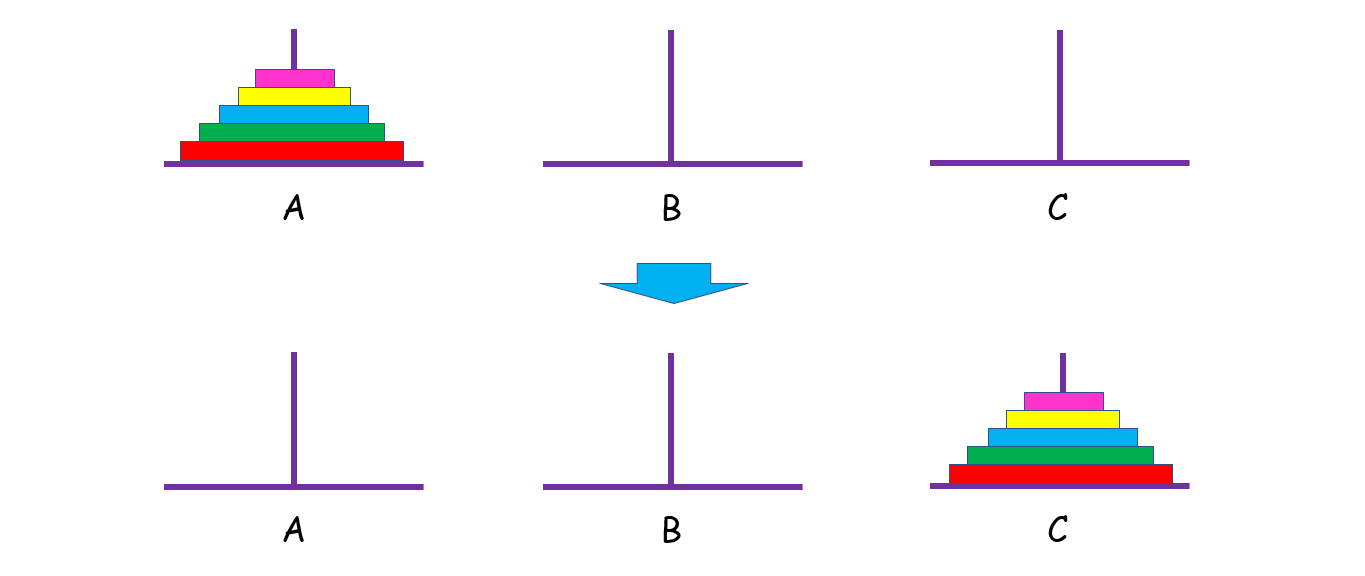
輸入：A = [2, 1, 0], B = [], C = []
輸出：C = [2, 1, 0]

解題思路：遞歸與分治
這是一道遞歸方法的經典題目，乍一想還挺難理清頭緒的，我們不妨先從簡單的入手。

假設 n = 1,只有一個盤子，很簡單，直接把它從 A 中拿出來，移到 C 上；

如果 n = 2 呢？這時候我們就要藉助 B 了，因為小盤子必須時刻都在大盤子上面，共需要 4 步。

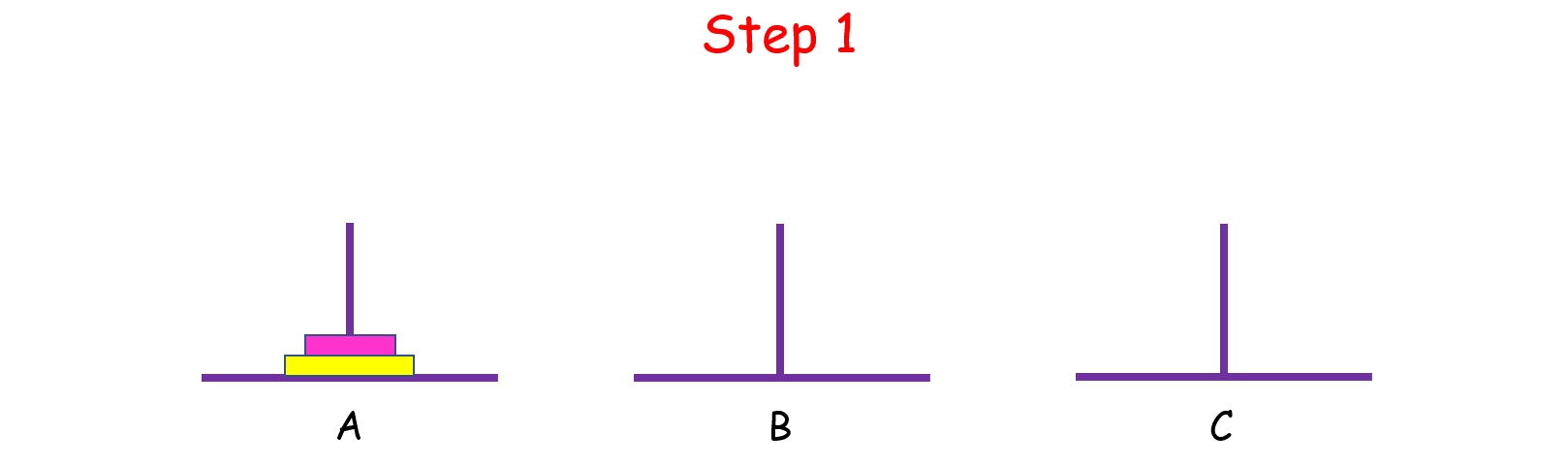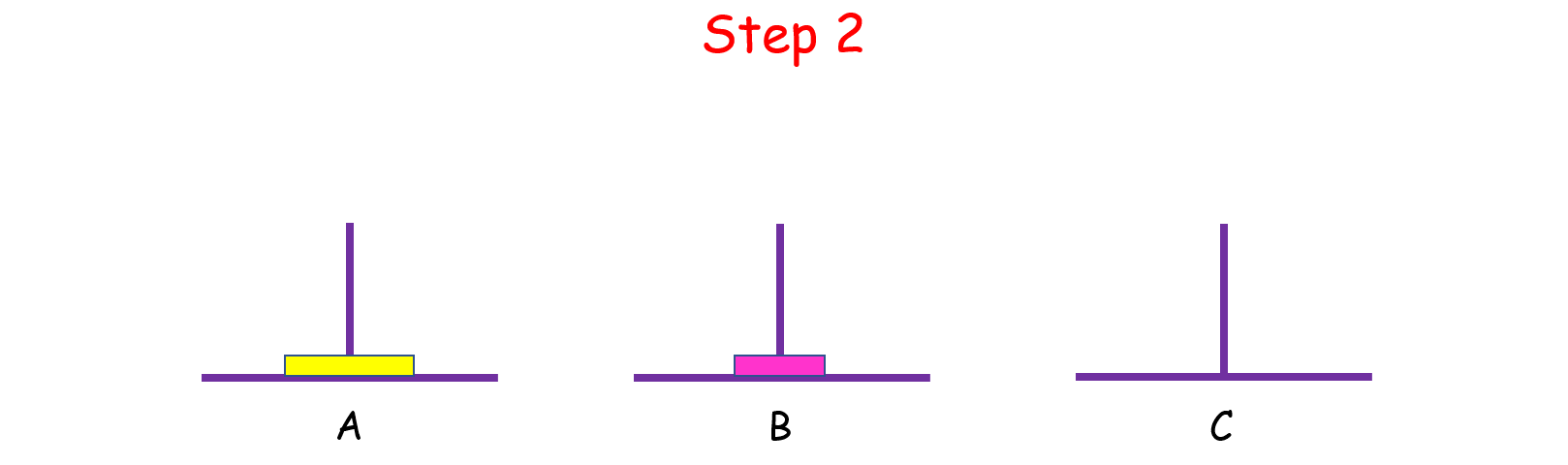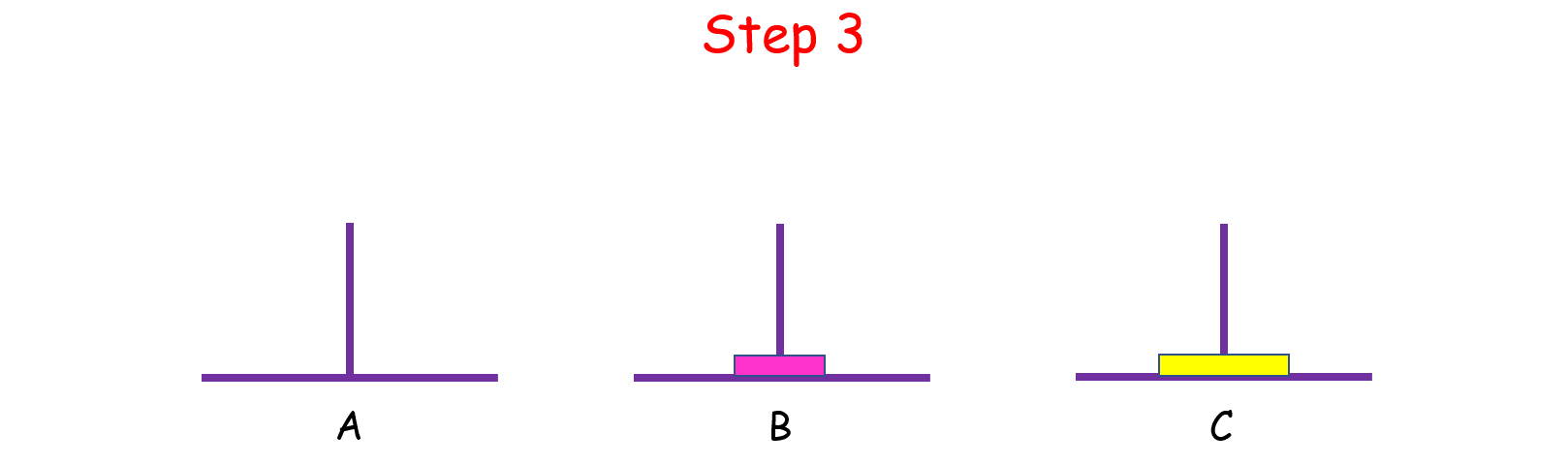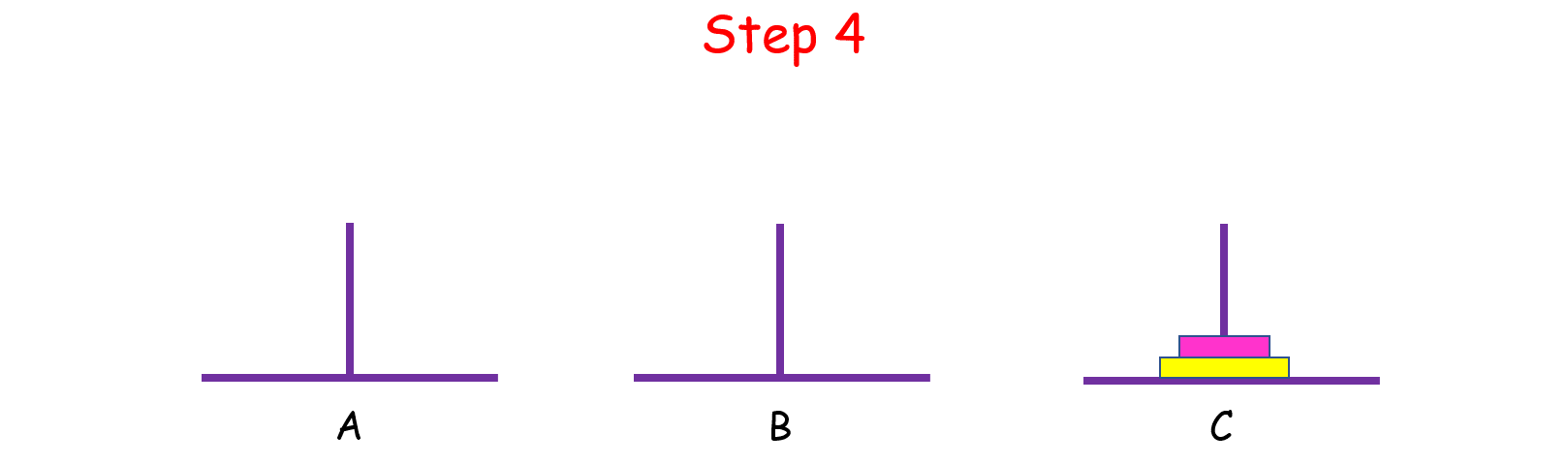
如果 n > 2 呢？思路和上面是一樣的，我們把 n 個盤子也看成兩個部分，一部分有 1 個盤子，另一部分有 n - 1 個盤子。

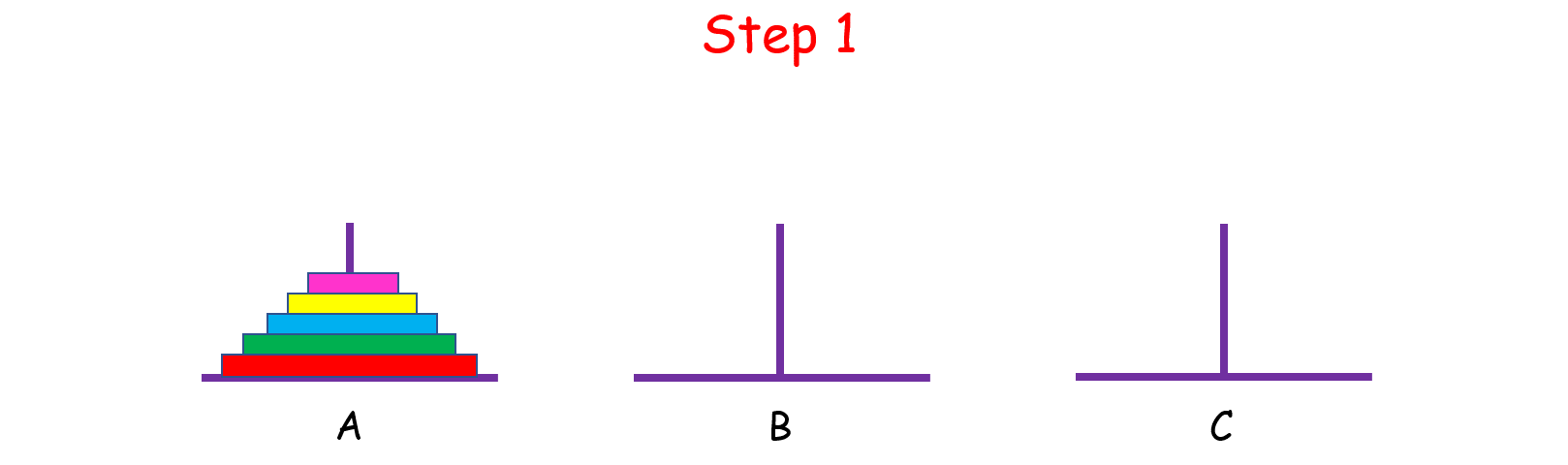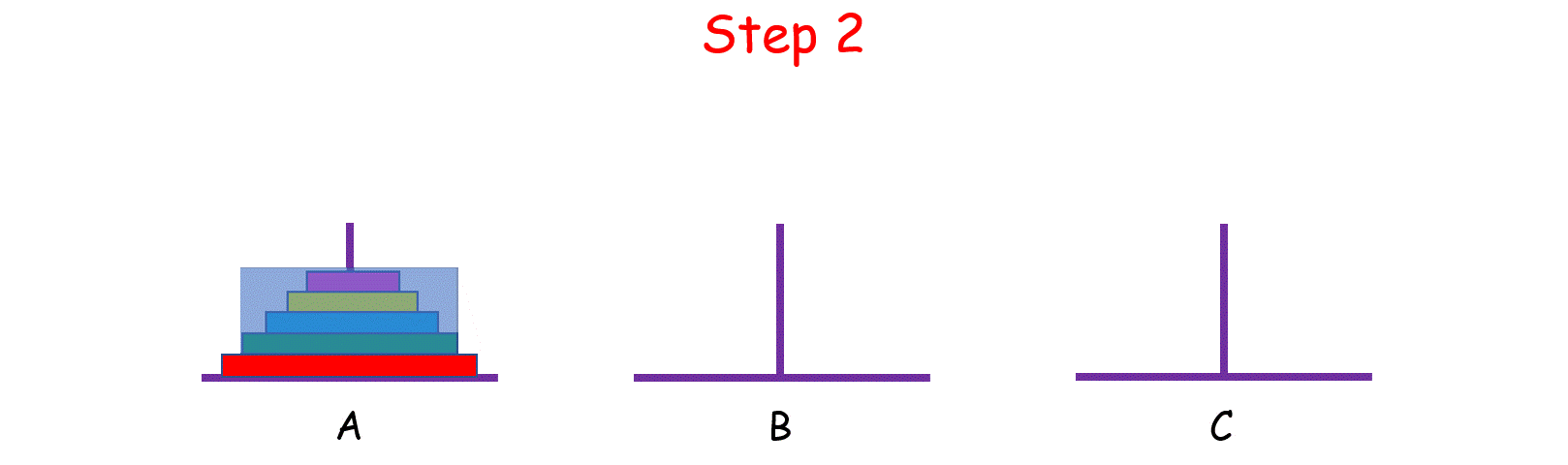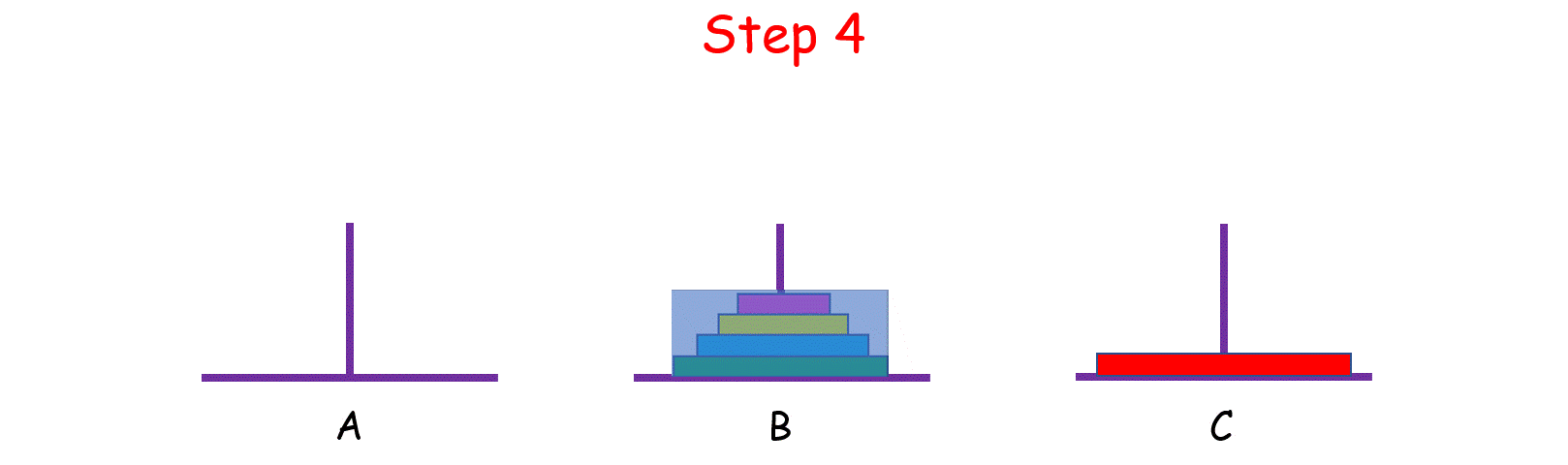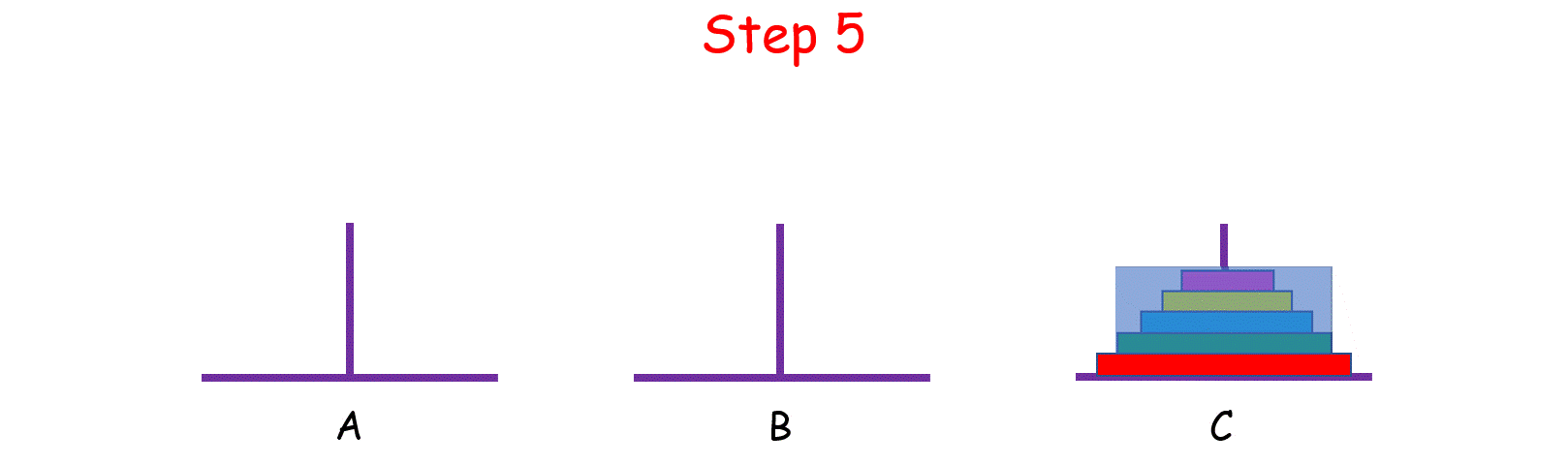
觀察上圖，你可能會問：“那 n - 1 個盤子是怎麼從 A 移到 C 的呢？”

當你在思考這個問題的時候，就將最初的 n 個盤子從 A 移到 C 的問題，轉化成了將 n - 1 個盤子從 A 移到 C 的問題， 依次類推，直至轉化成 1 個盤子的問題時，問題也就解決了。這就是分治的思想。

而實現分治思想的常用方法就是遞歸。不難發現，如果原問題可以分解成若幹個與原問題結構相同但規模較小的子問題時，往往可以用遞歸的方法解決。具體解決辦法如下：

• n = 1 時，直接把盤子從 A 移到 C；

• n > 1 時，

  • 先把上面 n - 1 個盤子從 A 移到 B（子問題，遞歸）；

  • 再將最大的盤子從 A 移到 C；

  • 再將 B 上 n - 1 個盤子從 B 移到 C（子問題，遞歸）。

Java代碼

class Solution {
    public void hanota(List<Integer> A, List<Integer> B, List<Integer> C) {
        /*
        1.先將A柱子中的n-1個的圓盤移動到B柱子
        2.再將A柱子中最後1個圓盤移動到C柱子
        3.最後將B柱子的n-1個圓盤移動到C柱子
         */
        int n = A.size();
        move(n, A, B, C);
    }

    /*
     其中A為原始柱子;B為輔助柱子;C為目標柱子(與位置有關,那麼list都有可能)
     */
    private void move(int n, List<Integer> A, List<Integer> B, List<Integer> C) {
        // A中只剩下1個圓盤了,直接移動到C柱子後結束
        if (n == 1) {
            C.add(A.remove(A.size() - 1));// 將A柱子中最後1個圓盤移動到C柱子
            return;
        }
        // 1.先將的A柱子中的n-1個的圓盤移動到B柱子(此時B為目標柱子,A為原始柱子)
        move(n - 1, A, C, B);
        // 2.再將的A柱子中最後1個圓盤移動到C柱子
        C.add(A.remove(A.size() - 1));
        // 3.最後將B柱子的n-1個圓盤移動到C柱子(此時C為目標柱子,B為原始柱子)
        move(n - 1, B, A, C);
    }
}

C++代碼

class Solution {
public:
    void hanota(vector<int>& A, vector<int>& B, vector<int>& C) {
        int n = A.size();
        move(n, A, B, C);
    }

    void move(int n, vector<int>& A, vector<int>& B, vector<int>& C){
        if (n == 1){
            C.push_back(A.back());
            A.pop_back();
            return;
        }

        move(n-1, A, C, B);    // 將A上面n-1個通過C移到B
        C.push_back(A.back());  // 將A最後一個移到C
        A.pop_back();          // 這時，A空了
        move(n-1, B, A, C);     // 將B上面n-1個通過空的A移到C
    }
};

複雜度分析

• 時間複雜度：O(2^n-1)。一共需要移動的次數。
• 空間複雜度：O(1)。