0. 前言 寫完這篇文章後發現自己對於 DP 的優化一竅不通,所以補了補 DP 的一些優化,寫篇 blog 總結一下。 1. 單調隊列/單調棧優化 1.2 演算法介紹 這應該算是最基礎的 DP 優化方法了。 顧名思義,單調隊列/單調棧優化 DP 就是保持容器內元素的單調性,以達成減少冗餘狀態的目的。 ...
0. 前言
寫完這篇文章後發現自己對於 DP 的優化一竅不通,所以補了補 DP 的一些優化,寫篇 blog 總結一下。
1. 單調隊列/單調棧優化
1.2 演算法介紹
這應該算是最基礎的 DP 優化方法了。
顧名思義,單調隊列/單調棧優化 DP 就是保持容器內元素的單調性,以達成減少冗餘狀態的目的。
舉單調隊列的例子來說,當一個元素的兩種屬性(例如下標和權值)都優於另一元素時,就可以用此元素更換掉另一元素。這也正是 OI 界流傳說法“當一個人比你小且比你強時,你就被彈出單調隊列了”的原理。
我們以下麵的例題作為例子來更具體地闡述這個演算法。
1.3 適用範圍&區別
一般來說,形如 \(f(i)=\max(f(j)+F(i)+F(j))\) 的式子都可以考慮適用單調隊列/單調棧進行優化。(其中 \(F(i)\) 和 \(F(j)\) 表示和 \(i,j\) 有關的函數)
應該大部分人剛學這兩種東西的時候都有一種疑惑:啥時候用單調隊列,啥時候用單調棧呢?(至少我有
其實,它們兩的本質區別還是其結構上的區別。單調棧通常用新加進來的東西替換掉一些棧頂元素,而單調隊列是可能兩端同時修改的。
在一下例題中我也會著重分析兩者的使用。
1.4 例題
I. P1886 滑動視窗
這個不是優化 DP,就是最經典的裸的不能再裸的單調隊列。
大力單調隊列即可,時間複雜度 \(O(n)\)。
II. CF372C Watching Fireworks is Fun
題目鏈接
OI Wili 推薦的題
題目大意:一個數軸上有 \(n\) 個點,每個點在位置 \(a_i\),有 \(m\) 個煙花要放,開始時間 \(t_i\)。你一開始的位置隨便,每一單位時間可以最多走 \(d\) 這麼多的距離,在 \(x\) 看到第 \(i\) 個煙花的快樂值為 \(b_i-|a_i-x|\),求最大的總代價。
數據範圍:\(n\leq 150000,m\leq 300\)。
看到這個數據範圍就知道大概是 \(O(nm)\) 的演算法(最多要卡卡常)。
我們容易設計出 DP 狀態 \(f(i,j)\) 表示放第 \(i\) 個煙花,位置在 \(j\) 時的最大快樂值。
轉移:\(f(i,j)=\max_{j-(t_i-t_{i-1})\cdot d_i\leq k\leq j+(t_i-t_{i-1})\cdot d_i}(f(i-1,k)+b_i-|a_i-j|)\)。
接下來就需要對 DP 進行優化了,首先因為當 \(i\) 和 \(j\) 確定時 \(b_i-|a_i-j|\) 可以看做常數,剩下的就可以用單調隊列去維護了。
註:本題使用單調隊列的原因為 \(k\) 兩邊都有限制,需要頭尾都更新。
時間複雜度 \(O(nm)\)。
III. P3572 [POI2014]PTA-Little Bird
IV. P1973 [NOI2011] NOI 嘉年華
V. P2254 [NOI2005] 瑰麗華爾茲
2. 斜率優化
斜率優化自己學過好幾遍,也聽 dalao 講過,但是總是感覺半懂不懂的。這次索性把它給搞徹底了罷……
2. 1 演算法介紹
以 OI Wiki 上的例題為例。
題目大意:有 \(n\) 個玩具,每個玩具有一個價值 \(c_i\)。你需要將這 \(n\) 個玩具分成若幹段,設一段 \([l,r]\) 的代價為 \((r-l+\sum_{i=l}^rc_i-L)^2\),其中 \(L\) 為常數,求最小的總代價。
數據範圍:\(n\leq 5\times 10^4\)
使用 DP 優化的一般思路:先設計出一個超時的 DP 再優化。
設 \(f_i\) 表示前 \(i\) 個玩具的代價,那麼得出轉移方程為:
\[f_i=\min_{j=0}^{i-1}\{f_j+(i-j-1+\sum_{k=j+1}^ic_k+L)^2\} \]用首碼和表示後即為:
\[f_i=\min_{j=0}^{i-1}\{f_j+(i-j-1+S_i-S_j+c_k+L)^2\} \]其中 \(S_i=\sum_{k=1}^ic_k\)。
這就是朴素的 \(O(n^2)\) 的 DP。
下麵就要優化了,不過有個問題:DP 跟斜率有什麼關係呢?
考慮將 DP 轉移方程轉化為解析幾何中直線的斜截式方程 \(y=kx+b\) 的形式。
我們先將只和 \(i,j\) 有關的歸為一類,常數歸為一類:\(a_i=s_i+i,b_i=s_i+i+L+1\),然後原式可以寫成:
\[f_i=\min_{j=0}^{i-1}\{f_j+(a_i-a_j)^2\} \]然後可以令 \(y=f_j+b_j^2,k=2a_i,x=b_j\)。(P.S. 這個應該只要滿足 \(y=kx+b\) 都可以?)
此時需要最小化直線的截距,先將這些 \((x,y)\) 表示在平面直角坐標系中:
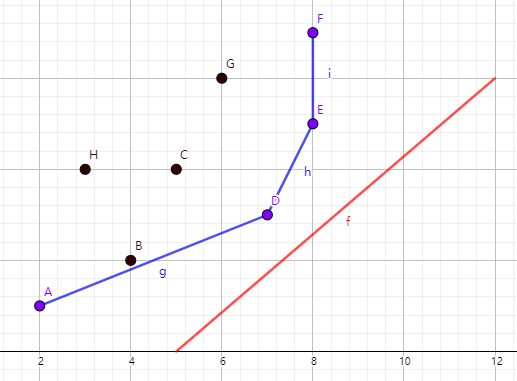
可以看到藍線連成了一個下凸殼,第一個紅線碰到的點使截距最小。
下麵的問題就是怎樣維護這個凸包,發現存在斜率遞增,所以可以用單調隊列來維護。
2.2 例題
I. P4072 [SDOI2016]征途
998244352. 參考資料
第 1 章:
第 2 章:
本文來自博客園,作者:Jerry_Jiang,轉載請註明原文鏈接:https://www.cnblogs.com/Jerry-Jiang/p/16565671.html



