https://blog.csdn.net/du5006150054/article/details/82379210 B+樹索引是B+樹在資料庫中的一種實現,是最常見也是資料庫中使用最為頻繁的一種索引。B+樹中的B代表平衡(balance),而不是二叉(binary),因為B+樹是從最早的平衡二叉 ...
https://blog.csdn.net/du5006150054/article/details/82379210
B+樹索引是B+樹在資料庫中的一種實現,是最常見也是資料庫中使用最為頻繁的一種索引。B+樹中的B代表平衡(balance),而不是二叉(binary),因為B+樹是從最早的平衡二叉樹演化而來的。在講B+樹之前必須先瞭解二叉查找樹、平衡二叉樹(AVLTree)和平衡多路查找樹(B-Tree),B+樹即由這些樹逐步優化而來。
二叉查找樹
二叉樹具有以下性質:左子樹的鍵值小於根的鍵值,右子樹的鍵值大於根的鍵值。
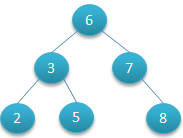
如下圖所示就是一棵二叉查找樹,
對該二叉樹的節點進行查找發現深度為1的節點的查找次數為1,深度為2的查找次數為2,深度為n的節點的查找次數為n,因此其平均查找次數為 (1+2+2+3+3+3) / 6 = 2.3次
二叉查找樹可以任意地構造,同樣是2,3,5,6,7,8這六個數字,也可以按照下圖的方式來構造:
但是這棵二叉樹的查詢效率就低了。因此若想二叉樹的查詢效率儘可能高,需要這棵二叉樹是平衡的,從而引出新的定義——平衡二叉樹,或稱AVL樹。
平衡二叉樹(AVL Tree)
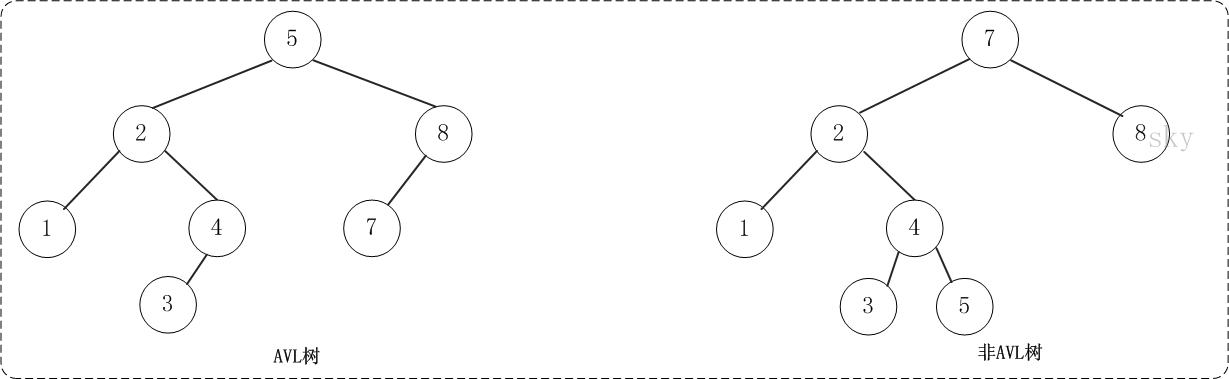
平衡二叉樹(AVL樹)在符合二叉查找樹的條件下,還滿足任何節點的兩個子樹的高度最大差為1。下麵的兩張圖片,左邊是AVL樹,它的任何節點的兩個子樹的高度差<=1;右邊的不是AVL樹,其根節點的左子樹高度為3,而右子樹高度為1;
如果在AVL樹中進行插入或刪除節點,可能導致AVL樹失去平衡,這種失去平衡的二叉樹可以概括為四種姿態:LL(左左)、RR(右右)、LR(左右)、RL(右左)。它們的示意圖如下:
這四種失去平衡的姿態都有各自的定義:
LL:LeftLeft,也稱“左左”。插入或刪除一個節點後,根節點的左孩子(Left Child)的左孩子(Left Child)還有非空節點,導致根節點的左子樹高度比右子樹高度高2,AVL樹失去平衡。
RR:RightRight,也稱“右右”。插入或刪除一個節點後,根節點的右孩子(Right Child)的右孩子(Right Child)還有非空節點,導致根節點的右子樹高度比左子樹高度高2,AVL樹失去平衡。
LR:LeftRight,也稱“左右”。插入或刪除一個節點後,根節點的左孩子(Left Child)的右孩子(Right Child)還有非空節點,導致根節點的左子樹高度比右子樹高度高2,AVL樹失去平衡。
RL:RightLeft,也稱“右左”。插入或刪除一個節點後,根節點的右孩子(Right Child)的左孩子(Left Child)還有非空節點,導致根節點的右子樹高度比左子樹高度高2,AVL樹失去平衡。
AVL樹失去平衡之後,可以通過旋轉使其恢復平衡。下麵分別介紹四種失去平衡的情況下對應的旋轉方法。
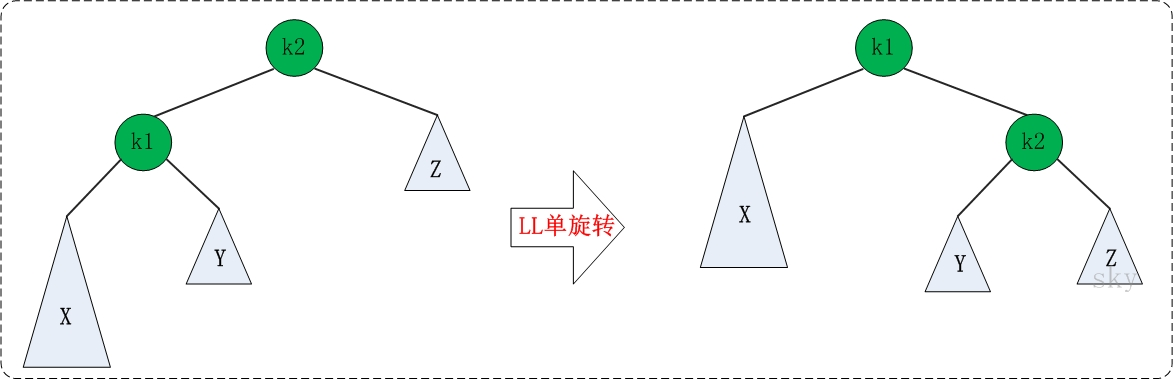
LL的旋轉。LL失去平衡的情況下,可以通過一次旋轉讓AVL樹恢復平衡。步驟如下:
- 將根節點的左孩子作為新根節點。
- 將新根節點的右孩子作為原根節點的左孩子。
- 將原根節點作為新根節點的右孩子。
LL旋轉示意圖如下:
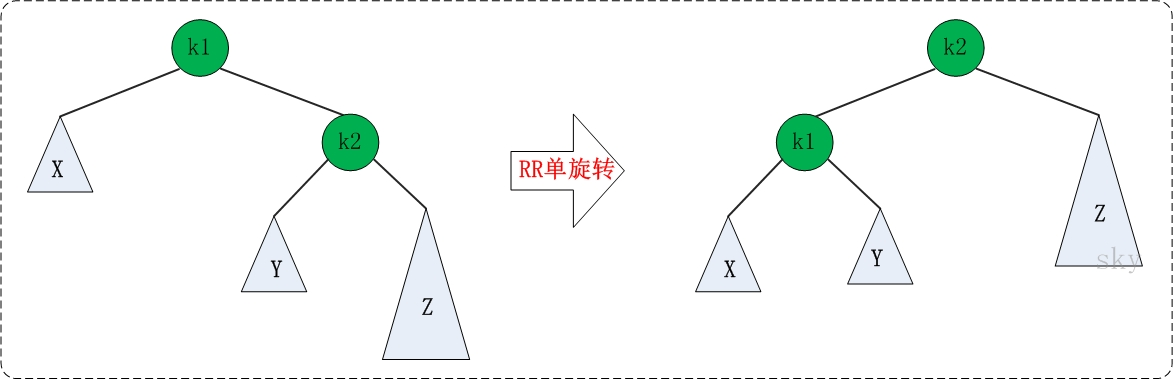
RR的旋轉:RR失去平衡的情況下,旋轉方法與LL旋轉對稱,步驟如下:
- 將根節點的右孩子作為新根節點。
- 將新根節點的左孩子作為原根節點的右孩子。
- 將原根節點作為新根節點的左孩子。
RR旋轉示意圖如下:
LR的旋轉:LR失去平衡的情況下,需要進行兩次旋轉,步驟如下:
- 圍繞根節點的左孩子進行RR旋轉。
- 圍繞根節點進行LL旋轉。
LR的旋轉示意圖如下:
RL的旋轉:RL失去平衡的情況下也需要進行兩次旋轉,旋轉方法與LR旋轉對稱,步驟如下:
- 圍繞根節點的右孩子進行LL旋轉。
- 圍繞根節點進行RR旋轉。
RL的旋轉示意圖如下:
平衡多路查找樹(B-Tree)
B-Tree是為磁碟等外存儲設備設計的一種平衡查找樹。因此在講B-Tree之前先瞭解下磁碟的相關知識。
系統從磁碟讀取數據到記憶體時是以磁碟塊(block)為基本單位的,位於同一個磁碟塊中的數據會被一次性讀取出來,而不是需要什麼取什麼。
InnoDB存儲引擎中有頁(Page)的概念,頁是其磁碟管理的最小單位。InnoDB存儲引擎中預設每個頁的大小為16KB,可通過參數innodb_page_size將頁的大小設置為4K、8K、16K,在MySQL中可通過如下命令查看頁的大小:
mysql> show variables like 'innodb_page_size';1- 1
而系統一個磁碟塊的存儲空間往往沒有這麼大,因此InnoDB每次申請磁碟空間時都會是若幹地址連續磁碟塊來達到頁的大小16KB。InnoDB在把磁碟數據讀入到磁碟時會以頁為基本單位,在查詢數據時如果一個頁中的每條數據都能有助於定位數據記錄的位置,這將會減少磁碟I/O次數,提高查詢效率。
B-Tree結構的數據可以讓系統高效的找到數據所在的磁碟塊。為了描述B-Tree,首先定義一條記錄為一個二元組[key, data] ,key為記錄的鍵值,對應表中的主鍵值,data為一行記錄中除主鍵外的數據。對於不同的記錄,key值互不相同。
一棵m階的B-Tree有如下特性:
\1. 每個節點最多有m個孩子。
\2. 除了根節點和葉子節點外,其它每個節點至少有Ceil(m/2)個孩子。
\3. 若根節點不是葉子節點,則至少有2個孩子
\4. 所有葉子節點都在同一層,且不包含其它關鍵字信息
\5. 每個非終端節點包含n個關鍵字信息(P0,P1,…Pn, k1,…kn)
\6. 關鍵字的個數n滿足:ceil(m/2)-1 <= n <= m-1
\7. ki(i=1,…n)為關鍵字,且關鍵字升序排序。
\8. Pi(i=1,…n)為指向子樹根節點的指針。P(i-1)指向的子樹的所有節點關鍵字均小於ki,但都大於k(i-1)
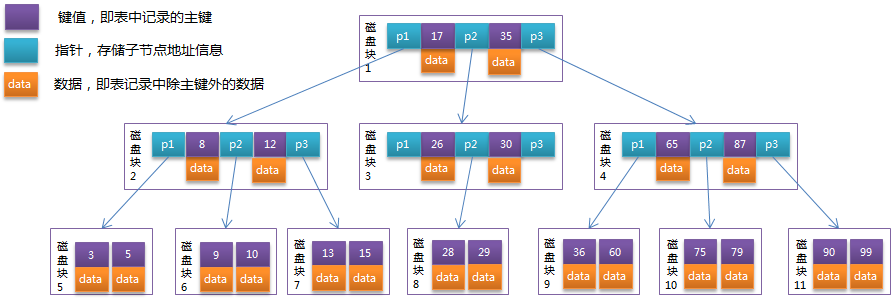
B-Tree中的每個節點根據實際情況可以包含大量的關鍵字信息和分支,如下圖所示為一個3階的B-Tree:
每個節點占用一個盤塊的磁碟空間,一個節點上有兩個升序排序的關鍵字和三個指向子樹根節點的指針,指針存儲的是子節點所在磁碟塊的地址。兩個關鍵詞劃分成的三個範圍域對應三個指針指向的子樹的數據的範圍域。以根節點為例,關鍵字為17和35,P1指針指向的子樹的數據範圍為小於17,P2指針指向的子樹的數據範圍為17~35,P3指針指向的子樹的數據範圍為大於35。
模擬查找關鍵字29的過程:
- 根據根節點找到磁碟塊1,讀入記憶體。【磁碟I/O操作第1次】
- 比較關鍵字29在區間(17,35),找到磁碟塊1的指針P2。
- 根據P2指針找到磁碟塊3,讀入記憶體。【磁碟I/O操作第2次】
- 比較關鍵字29在區間(26,30),找到磁碟塊3的指針P2。
- 根據P2指針找到磁碟塊8,讀入記憶體。【磁碟I/O操作第3次】
- 在磁碟塊8中的關鍵字列表中找到關鍵字29。
分析上面過程,發現需要3次磁碟I/O操作,和3次記憶體查找操作。由於記憶體中的關鍵字是一個有序表結構,可以利用二分法查找提高效率。而3次磁碟I/O操作是影響整個B-Tree查找效率的決定因素。B-Tree相對於AVLTree縮減了節點個數,使每次磁碟I/O取到記憶體的數據都發揮了作用,從而提高了查詢效率。
B+Tree
B+Tree是在B-Tree基礎上的一種優化,使其更適合實現外存儲索引結構,InnoDB存儲引擎就是用B+Tree實現其索引結構。
從上一節中的B-Tree結構圖中可以看到每個節點中不僅包含數據的key值,還有data值。而每一個頁的存儲空間是有限的,如果data數據較大時將會導致每個節點(即一個頁)能存儲的key的數量很小,當存儲的數據量很大時同樣會導致B-Tree的深度較大,增大查詢時的磁碟I/O次數,進而影響查詢效率。在B+Tree中,所有數據記錄節點都是按照鍵值大小順序存放在同一層的葉子節點上,而非葉子節點上只存儲key值信息,這樣可以大大加大每個節點存儲的key值數量,降低B+Tree的高度。
B+Tree相對於B-Tree有幾點不同:
- 非葉子節點只存儲鍵值信息。
- 所有葉子節點之間都有一個鏈指針。
- 數據記錄都存放在葉子節點中。
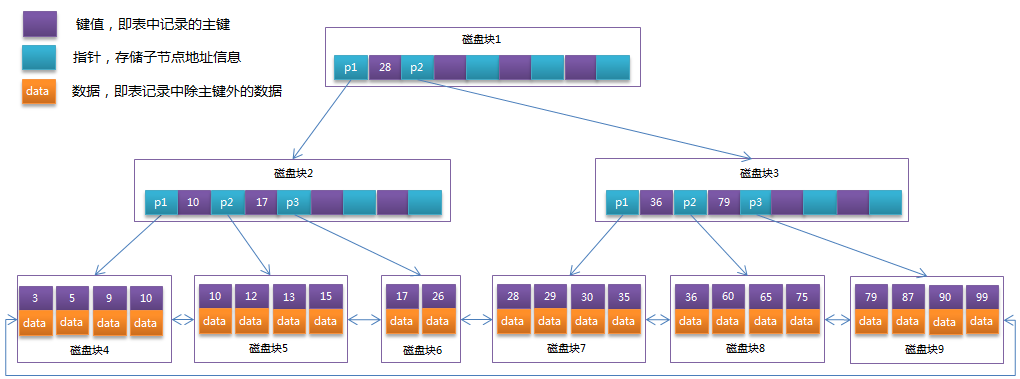
將上一節中的B-Tree優化,由於B+Tree的非葉子節點只存儲鍵值信息,假設每個磁碟塊能存儲4個鍵值及指針信息,則變成B+Tree後其結構如下圖所示:
通常在B+Tree上有兩個頭指針,一個指向根節點,另一個指向關鍵字最小的葉子節點,而且所有葉子節點(即數據節點)之間是一種鏈式環結構。因此可以對B+Tree進行兩種查找運算:一種是對於主鍵的範圍查找和分頁查找,另一種是從根節點開始,進行隨機查找。
可能上面例子中只有22條數據記錄,看不出B+Tree的優點,下麵做一個推算:
InnoDB存儲引擎中頁的大小為16KB,一般表的主鍵類型為INT(占用4個位元組)或BIGINT(占用8個位元組),指針類型也一般為4或8個位元組,也就是說一個頁(B+Tree中的一個節點)中大概存儲16KB/(8B+8B)=1K個鍵值(因為是估值,為方便計算,這裡的K取值為〖10〗^3)。也就是說一個深度為3的B+Tree索引可以維護10^3 * 10^3 * 10^3 = 10億 條記錄。
實際情況中每個節點可能不能填充滿,因此在資料庫中,B+Tree的高度一般都在2~4層。MySQL的InnoDB存儲引擎在設計時是將根節點常駐記憶體的,也就是說查找某一鍵值的行記錄時最多只需要1~3次磁碟I/O操作。
資料庫中的B+Tree索引可以分為聚集索引(clustered index)和輔助索引(secondary index)。上面的B+Tree示例圖在資料庫中的實現即為聚集索引,聚集索引的B+Tree中的葉子節點存放的是整張表的行記錄數據。輔助索引與聚集索引的區別在於輔助索引的葉子節點並不包含行記錄的全部數據,而是存儲相應行數據的聚集索引鍵,即主鍵。當通過輔助索引來查詢數據時,InnoDB存儲引擎會遍歷輔助索引找到主鍵,然後再通過主鍵在聚集索引中找到完整的行記錄數據