初級模擬電路：4-6 共射放大電路（交流分析）

回到目錄

      比起共基放大電路，共射放大電路稍微要複雜一些，有若幹種偏置形式，但萬變不離其宗，分析的基本原理都是一致的，本小節我們對三種典型的共射偏置形式進行交流分析，分別是：固定偏置、射極偏置（改進的固定偏置）、分壓偏置。

1. 固定偏置

      固定偏置的共射放大電路如下圖所示：

圖4-6.01 

      註意在上圖中的各個電壓電流符號，有的僅含小信號交流分量，有的同時包含小信號交流分量和直流分量。集電極電阻R_C起到了負載電阻的作用，故輸出電流i_o從R_C上通過。而C₂的作用僅在於隔離直流取出交流輸出電壓v_o，並無電流通過。而且從上圖可以很明顯的看出，輸入電流i_i就等於基級電流的交流電流i_b，輸出電流i_o就等於集電極電流的交流分量i_c。

      在交流分析中，電容C₁和C₂可視為短路，直流電壓源可視為直接通地，將上圖中的BJT晶體管替換成r_e等效模型後的交流等效電路如下圖所示（註意下圖中的所有電量符號都變成了交流的相量形式）：

圖4-6.02 

● 輸入阻抗：

      從上圖中可以很容易地看出，輸入阻抗為：

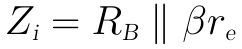
      在固定偏置情況下，由於基級電流非常微小，所以一般會將R_B配得比較大（通常為幾百kΩ左右），大多數情況下都會大於10倍的βr_e，因此在一些要求不高的場合下，可忽略R_B而認為輸入阻抗近似為：

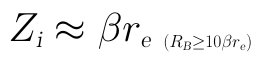
● 輸出阻抗：

      前一小節我們說過，在共射組態中，BJT晶體管的固有輸出電阻r_o大約為幾十kΩ級，一般不能忽略不計，故在上圖的等效電路中畫出了r_o的存在。當輸入V_i=0時，I_b=0，受控電流源βI_b=0，可視為開路，因此輸出阻抗為：

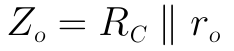
      但是，有時在配置集電極電阻R_C時，如果將R_C的值選取得比較小，當R_C的值小於10倍的r_o時，這時可將r_o近似看作開路，而近似忽略r_o的存在。

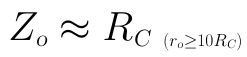
● 電壓放大倍數：

      輸入電壓V_i和輸出電壓V_o的表達式分別為：

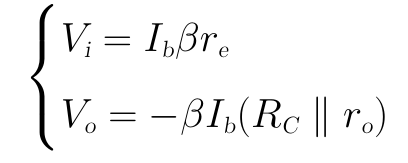
      電壓放大倍數為：

      和前面類似，當R_C的值取得比較小時，電壓放大倍數可近似為：

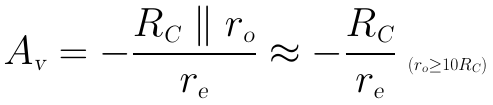
      上式中的負號表明，輸出電壓和輸入電壓的反向，或者稱：輸出信號和輸入信號之間存在180°的相移。

案例4-6-1：對於下圖的固定偏置共射放大電路，使用r_e等效模型試求：（1）r_e的值；（2）輸入阻抗Z_i；（3）輸出阻抗Z_o（對r_o=∞和r_o=50kΩ兩種情況分別求值）；（4）電壓放大倍數A_v（對r_o=∞和r_o=50kΩ兩種情況分別求值）。

圖4-06.a1 

解：（1）r_e的值由流過三極體發射結的靜態工作電流（即I_E）決定：

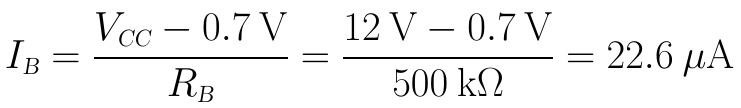
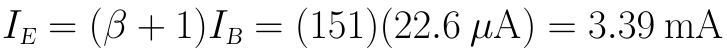
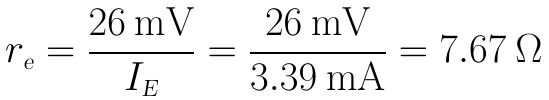
（2）先求βr_e：

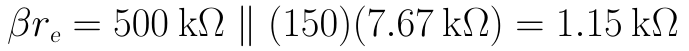
      輸入阻抗Z_i為：

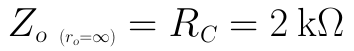
      可見，當R_B取值為幾百kΩ時，R_B對輸入阻抗的影響及其微小。

（3）當r_o=∞時，輸出阻抗Z_o為：

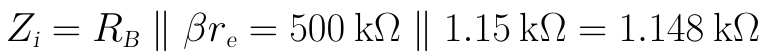
      當r_o=50kΩ時，輸出阻抗Z_o為：

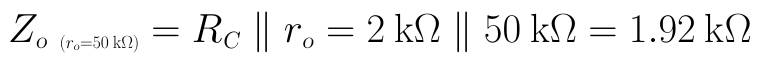
      比較可見，當計入r_o的影響時，輸出阻抗會略為減小。

（4）當r_o=∞時，電壓放大繫數A_v為：

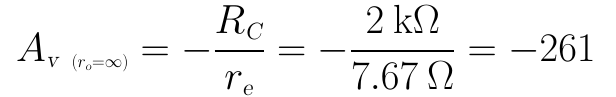
      當r_o=50kΩ時，電壓放大繫數A_v為：

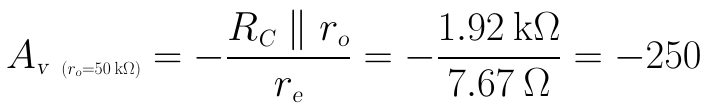
      比較可見，當計入r_o的影響時，電壓放大倍數會有所減小。

2. 射極偏置

（1）基本分析

      我們曾在共射放大電路的直流分析章節講過，在固定偏置的發射極增加一個射極電阻R_E，可以大大提高電路的穩定性，這種改進的固定偏置形式也稱為射極偏置。本小節我們就對射極偏置電路進行交流分析。

      下圖是一個射極偏置共射放大電路的基本電路：

圖4-06.03 

      將上圖中的BJT晶體管替換成r_e等效模型後的交流等效電路如下圖所示：

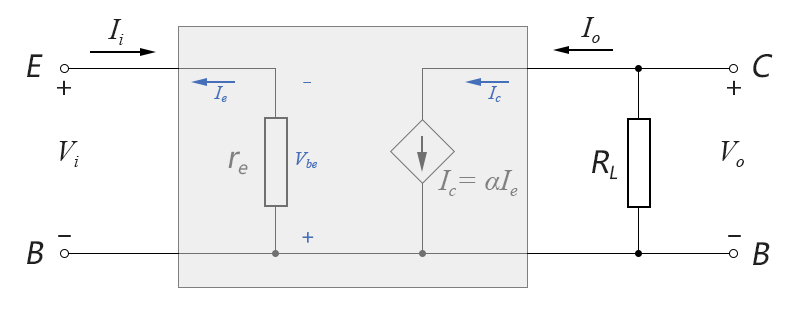
圖4-06.04 

      上圖中，為分析簡便起見，我們先不考慮輸出電阻r_o的影響，將其視為無窮大（因為在有射極電阻R_E的情況下，在r_e模型中加上r_o後，會使電路的計算複雜度大大增加，不利於我們概念的說明，後文我們會專門討論當考慮r_o的影響時如何計算）。

● 輸入阻抗：

      這裡輸入阻抗直接用V_i/I_i的公式進行強推比較困難，我們可以先作一下變通，先求出不含R_B時，直接從BJT輸入端看入的“僅BJT的輸入阻抗”Z_b，然後再用Z_b和R_B並聯即可得到整個電路的輸入阻抗Z_i。

      對BJT的輸入端列寫KVL方程可得：

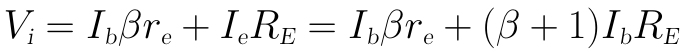
      則從BJT輸入端看入的等效電阻Z_b為：

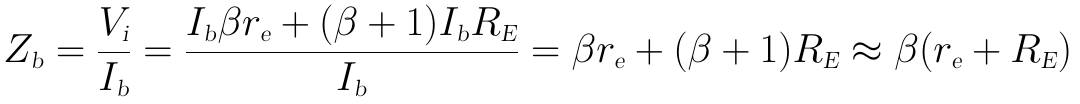
      通常R_E為kΩ級，遠大於幾個歐姆級的r_e，如果需要的話，上式可進一步近似為：

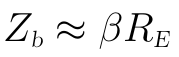
      算出Z_b後，輸入阻抗為R_B和Z_b的並聯：

● 輸出阻抗：

      當不考慮r_o的影響時，輸出阻抗的計算比較簡單。當輸入V_i=0時，I_b=0，受控電流源βI_b=0，可視為開路，因此輸出阻抗即為：

● 電壓放大倍數：

      方法和前面類似，我們先算出輸入電壓V_i和輸出電壓V_o的表達式：

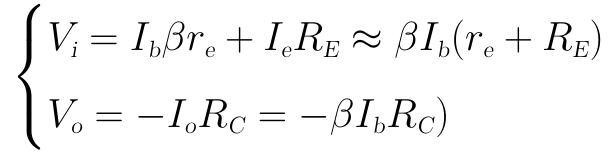
      電壓放大倍數即為：

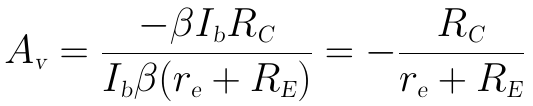
      當R_E≥10r_e時，上式可進一步近似為：

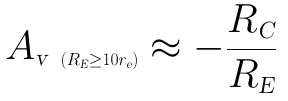
      上式中的負號表明，輸出電壓和輸入電壓的反向，或者稱：輸出信號和輸入信號之間存在180°的相移。

（2）增加旁路電容

      在上面的射極偏置電路中，我們觀察電壓放大倍數：

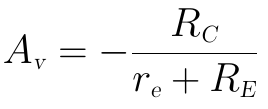
      一般R_C的選值為幾個kΩ級（在案例4-6.a1中，R_C=2kΩ）,而R_E一般會選取幾百歐到kΩ級（比如選0.5kΩ），代入上式後計算得：

      這樣的電壓放大倍數也太小了，非常不實用。

      我們回憶一下直流分析時的情形，當時固定偏置電路的主要問題是靜態工作點不穩，增加射極電阻的目的是為了提高電路的穩定性。但現在增加了射極電阻後，又發現射極電阻R_E會導致（交流）電壓放大倍數大為減小。

      那麼有什麼辦法可以解決這個問題麽？答案是有的。人們對射極偏置電路進行了改進，在射極電阻旁增加了一個旁路電容，發明瞭“帶射極旁路電容的射極偏置電路”，如下圖所示：

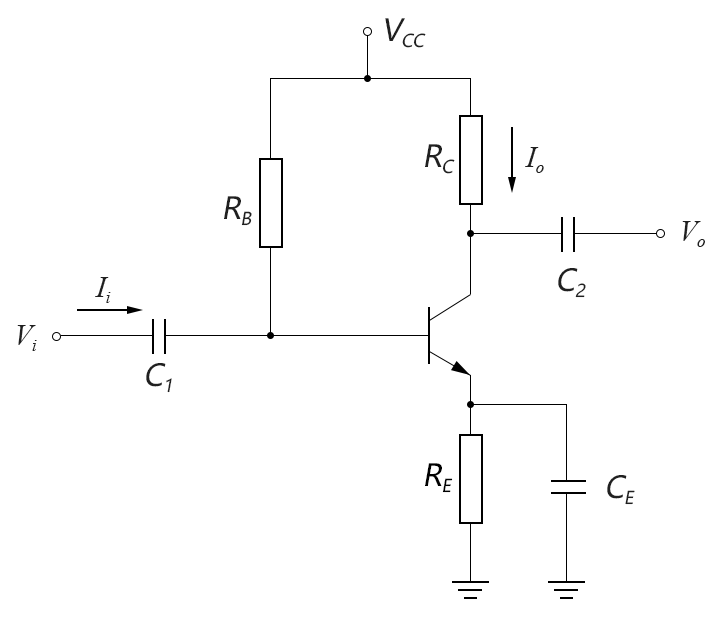
圖4-06.05 

      這時候你就會看到交直流分開的好處了：在直流分析時，由於電容的隔直屬性，就好像電容C_E不存在一樣，可以盡享射極電阻R_E帶來的好處；在交流分析時，由於電容的交流短路屬性，就好像射極電阻R_E被射極旁路電容C_E短路掉一樣，因此交流電壓放大倍數的計算式就成為了：

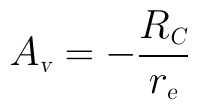
      等於是消除了射極電阻R_E對電壓放大倍數帶來的不利影響。

      堪稱精妙的設計！

案例4-6-2：對於下圖的射極偏置共射放大電路，使用r_e等效模型試求：（1）r_e的值；（2）輸入阻抗Z_i；（3）輸出阻抗Z_o；（4）電壓放大倍數A_v（對不含和含有射極旁路電容兩種情況分別求值）。

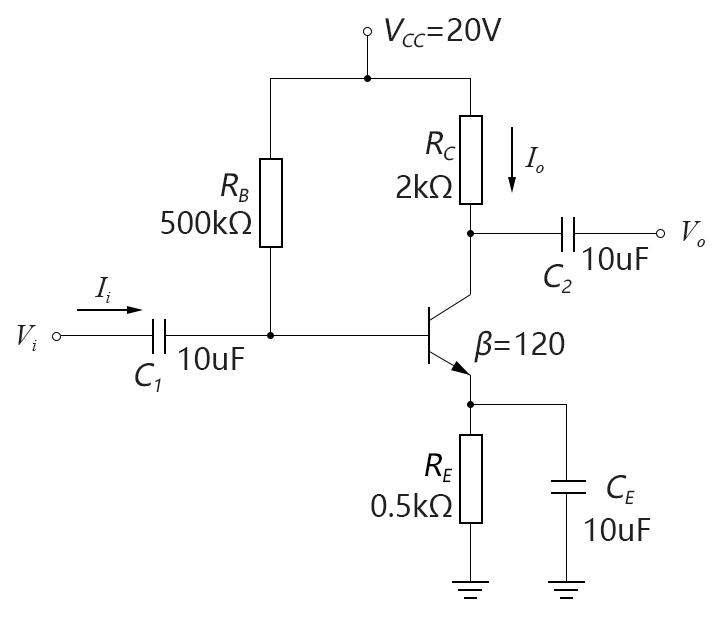
圖4-06.a2 

解：（1）r_e的值由流過三極體發射結的靜態工作電流（即I_E）決定：

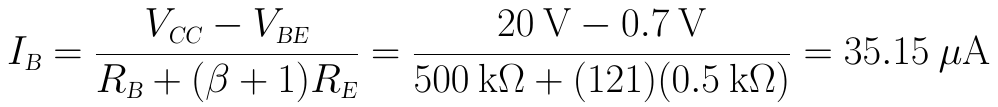
（2）輸入阻抗為R_B和Z_b的並聯：

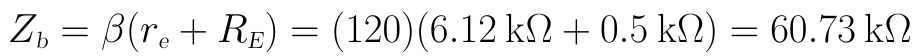
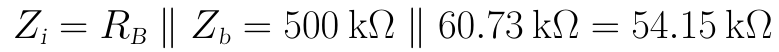
（3）輸出阻抗為Z_o為：

（4）不含射極旁路電容時，電壓放大倍數為：

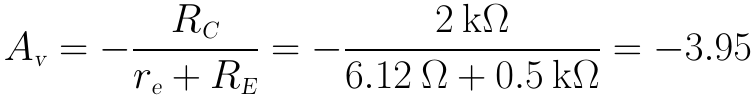
      當含有射極旁路電容時，電壓放大倍數為

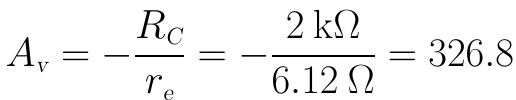
      兩者比較一下就可看出，有射極旁路電容時，電壓放大倍數明顯增大。

      射極偏置放大電路的一種改進型如下圖所示：

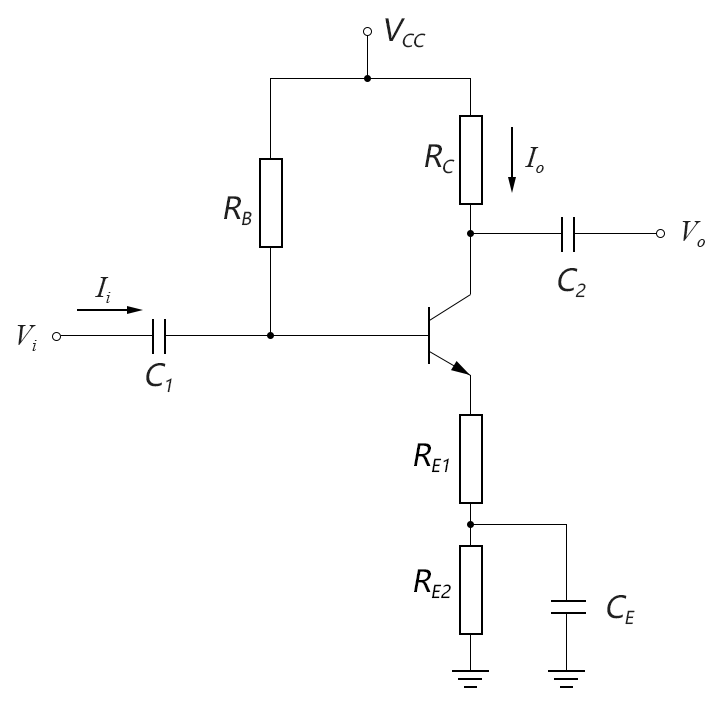
圖4-06.06 

      這樣做的好處是，可以通過R_E1的取值來更精確地調節電壓放大倍數，這種改進型的射極偏置電路的電壓放大倍數的計算式為：

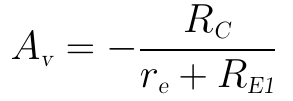
      可見，其改進後的電壓放大倍數A_v比無射極旁路電容時要大，比有射極旁路電容時要小，性能介於兩者之間，比較折中。

（3）輸出電阻r_o的影響

      前面的各個計算結果都為不考慮BJT固有輸出電阻r_o時的計算公式，一般情況下也夠用了。本小節將展示一下，如果把r_o考慮進去，計算過程會有多複雜。

      提示：前方高能預警，暈密集公式症者可跳過本小節，不影響後續章節的理解。不過，如果你耐心一點，願意多用點草稿紙，一步步按步就搬地推算，其實也不難。

      ……

      ……

      ……

      好，現在正式開始。當考慮輸出電阻r_o時，前面“圖4-06.04”的r_e模型等效電路將變成如下形式：

圖4-06.07 

● 輸入阻抗：

      總輸入阻抗的演算法和前面類似，為R_B和Z_b的並聯，但是Z_b的的計算式將大為複雜。我們將上圖中無關的部分略去，僅畫出和計算Z_b有關的部分：

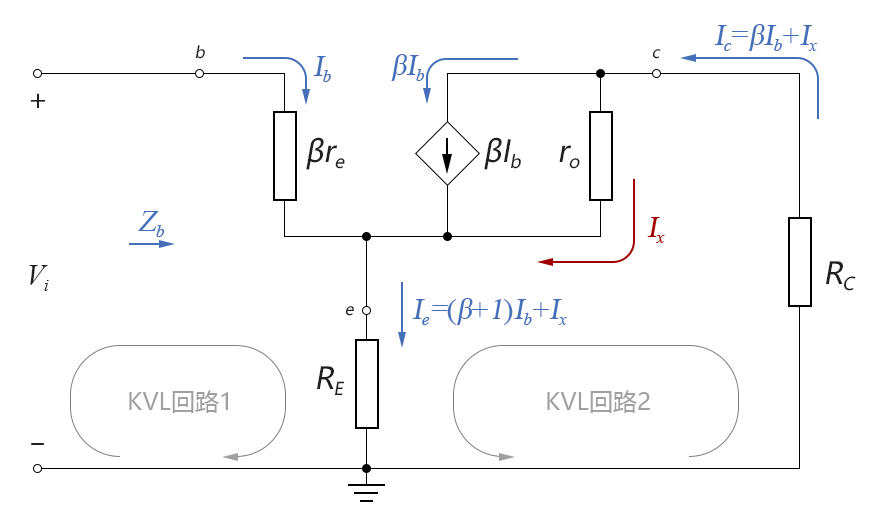
圖4-06.08 

      註意：在上圖中，由於r_o的存在，I_c不再嚴格等於βI_b，而是等於βI_b+I_x。回憶一下我們在第3章對β參數的定義：交流β參數近似等於直流β參數，但並不嚴格相等，原因就在這裡。同樣的，在這裡I_e也不再嚴格等於(β+1)I_b，而是等於：(β+1)I_b+I_x。

      我們先對KVL迴路1列寫方程式：

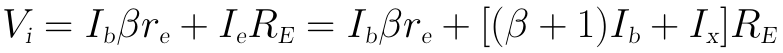
      上式稍微歸併一下可得：

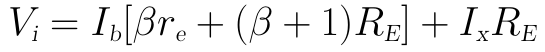
      然後對KVL迴路2列寫方程式：

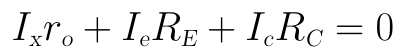
      將圖中的I_c和I_e分別代入上式可得：

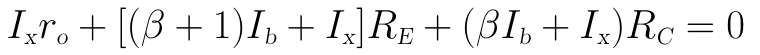
      上式稍微歸併一下可得：

      將這個I_x代入上面KVL迴路1的歸併式，可得：

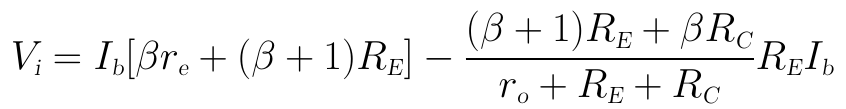
      得到上式後，就可以利用V_i/I_b來計算BJT的輸入阻抗Z_b了，上式稍微化簡一下可得：

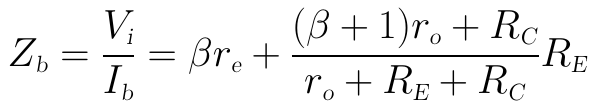
      這個就是考慮r_o後的純BJT輸入阻抗Z_b的表達式。然後再將這個值與R_B並聯，就可得到最終的輸入阻抗Z_i的完整表達式：

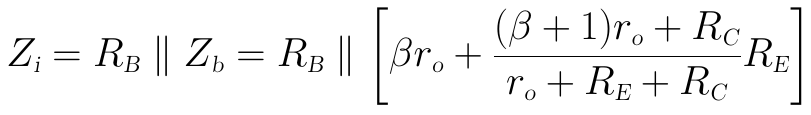
      怎麼樣？是不是已經用掉幾大張草稿紙了？然後我們考慮在什麼情況下可以對Z_b進行近似：

      將Z_b表達式右邊的分式中的分子分母同時除以r_o，可得：

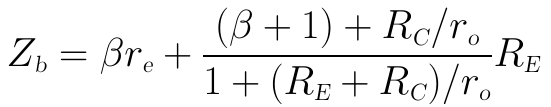
      由於R_C一般為幾個kΩ級、r_o一般為幾十個kΩ級，R_C/r_o通常遠小於(β+1)，故分子可近似為(β+1)。而R_E一般為和R_C為同一量級，若取10(R_E+R_C)≤r_o時，分母可近似為1，故上式可近似為：

      這個結果就是前面不考慮r_o時的射極偏置得到的結果。

● 輸出阻抗：

      與計算輸入阻抗類似，輸出阻抗可以看作R_C和Z_c的並聯，其中Z_c為從BJT的集電極看入的純BJT輸出阻抗。同樣的，Z_c的計算也相當複雜，我們下麵採用標準方法計算純BJT的輸出阻抗Z_c：首先將輸入端V_i短接，然後在輸出端施加一個U_o的外電源，通過計算U_o/I_o來計算Z_c。

      去掉無關部分的等效電路如下圖所示：

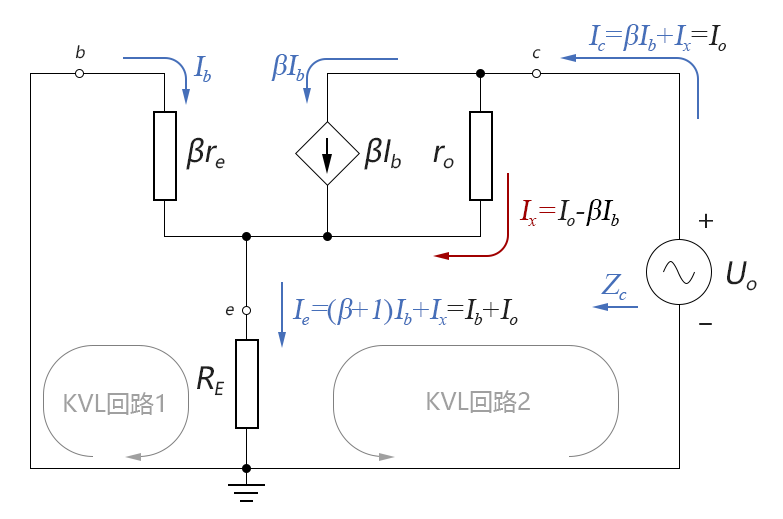
圖4-06.09 

      我們先對KVL迴路1列寫方程式：

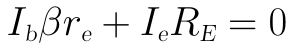
      將圖中的I_e=I_b+I_o代入上式可得：

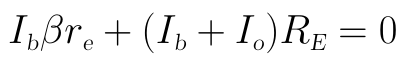
      將上式歸併一下可得到I_b和I_o的關係式：

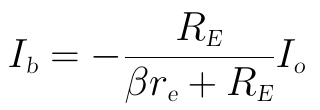
      然後對KVL迴路2列寫方程式：

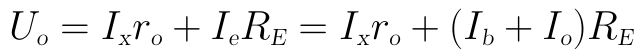
      將圖中的I_x=I_o-βI_b代入上式可得：

      再將前面算得得I_b與I_o的關係式代入上式可得：

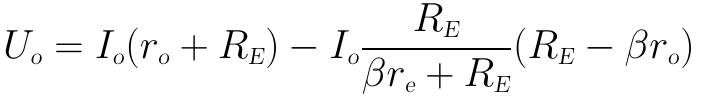
      將上式中的I_o移到等式右邊，再進行一些歸併，即可得到BJT的輸出阻抗Z_c：

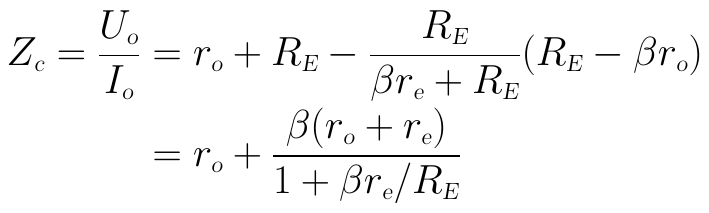
      這個就是考慮r_o後的純BJT輸出阻抗Z_c的表達式。然後再將這個值與R_C並聯，就可得到最終的輸出阻抗Z_o的完整表達式：

      然後我們考慮在什麼情況下可以對ZC進行近似：

      在上式中，由於r_o一般為幾十kΩ級，而r_e為幾個歐姆級，故Z_c可近似為：

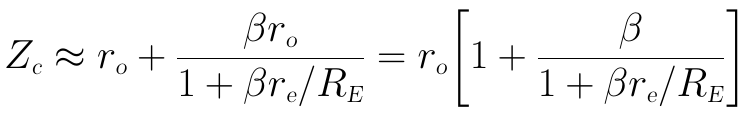
      將上式右邊的分式中的分子分母同除以β，可以得到：

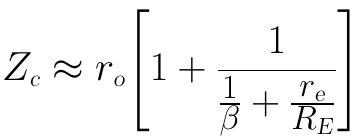
      通常1/β和r_e/R_E都是比1小很多的小數，1除以這兩個分式之和通常都會達到幾十或幾百，最終使得Z_c為幾十倍或幾百倍的r_o，因此Z_o最終可近似為：

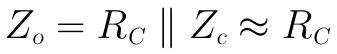
      這個結果就是前面不考慮r_o時的射極偏置得到的結果。

● 電壓放大倍數：

      電壓放大倍數為V_o和V_i的比值，我們重畫電路圖如下：

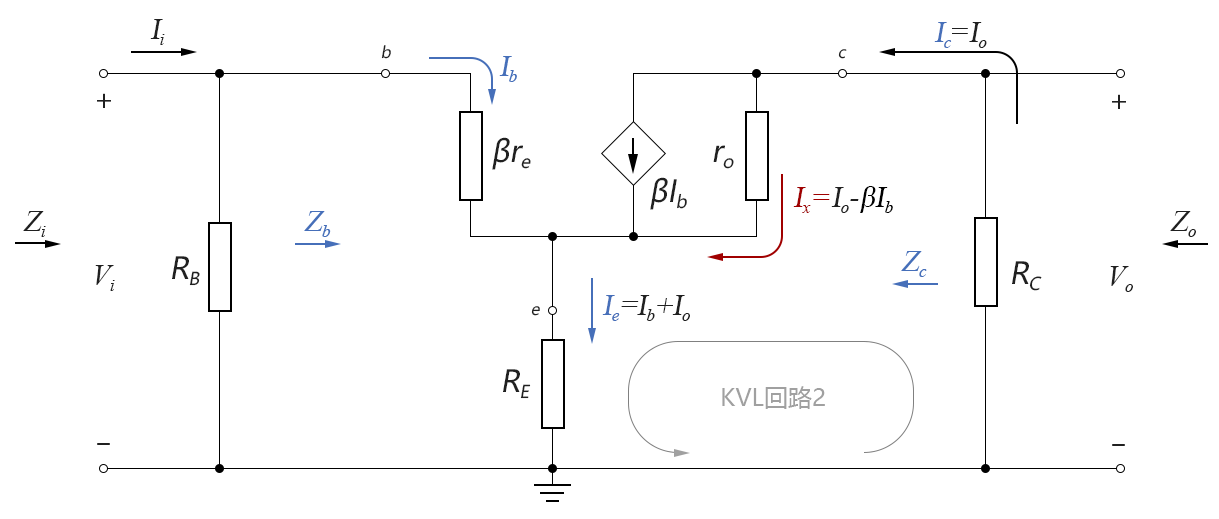
圖4-06.10 

      計算輸入電壓時，我們可利用先前算得的中間結果Z_b：

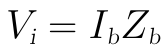
      輸出電壓為：

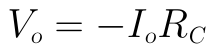
      為使V_o與V_i可以相除時可以消去I_b和I_o，我們還需要對KVL迴路2列寫方程式，以得到I_b和I_o的關係式：

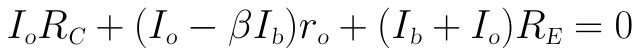
      歸併後可得：

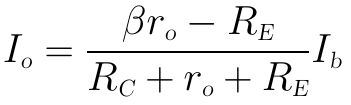
      因此，電壓放大倍數為：

      然後我們考慮近似情況，當r_o≥10 (R_C+R_E)時，上式可近似為：

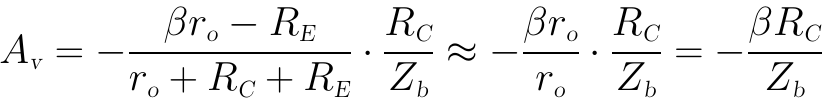
      再前面算得的Z_b的近似結果代入上式可得：

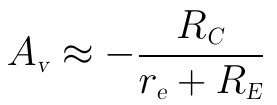
      這個結果就是前面不考慮r_o時的射極偏置得到的結果。

      好了，這個就是考慮r_o後的各個參數的計算過程，跟前面不考慮r_o時的計算比起來是不是酸爽得多？其實，如果你以後有機會學一下初級數字信號處理（DSP）的內容的話，你會發現這些公式推導的工作量和那個比起來簡直是小巫見大巫。

      在複雜公式推導的過程中，上式和下式之間需要大量的傳遞抄寫，最怕的就是抄錯一個量，之後整個推導就會失敗。所以，小學語文老師叫你字寫得工整一點、好看一點，現在知道用處了吧，那個基礎技能點掌握得好，對你後期攀升科技樹其實是很有幫助的。

3. 分壓偏置

      分壓偏置的共射放大電路如下圖所示：

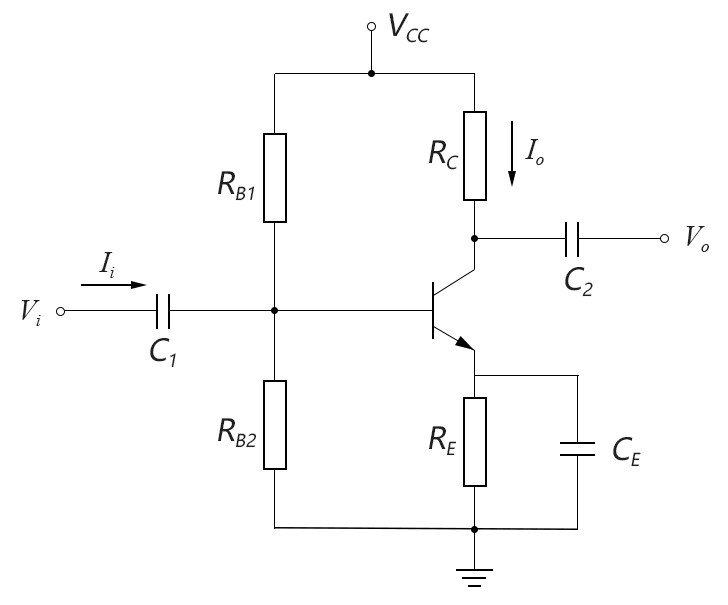
圖4-06.11 

      將上圖中的BJT晶體管替換成r_e等效模型後的交流等效電路如下圖所示（註意下圖中的所有電量符號都變成了交流的相量形式）：

圖4-06.12 

● 輸入阻抗：

      從上圖可以很容易看出，輸入阻抗為：

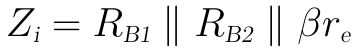
● 輸出阻抗：

      當將輸入電壓V_i置0時，I_b=0，受控電流源βI_b=0，可視為開路，因此輸出阻抗為：

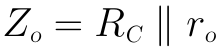
      當R_C的值小於10倍的r_o時，可作如下近似：

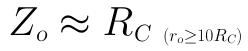
● 電壓放大倍數：

      輸入電壓V_i和輸出電壓V_o的表達式分別為：

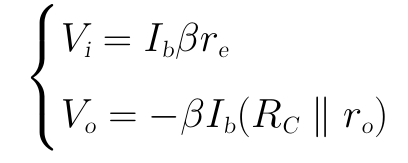
      電壓放大倍數為：

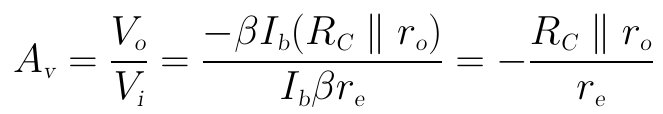
      當R_C的值取得比較小時，電壓放大倍數可近似為：

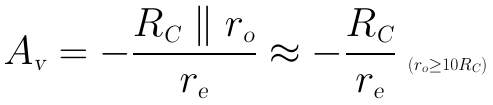
      電壓放大倍數的結果與“固定偏置”的結果完全相同。

回到目錄

歡迎關註本博公眾號，可方便在手機端訪問和索引本博技術文章：

（ end of 4-6）