回到目錄 1. 交流分析與交流電阻 我們曾經在 1-4二極體的電阻 大致講過交流電阻的特性,交流電阻並不是一個實際的可直接測量的物理量,而是一個抽象的量(是伏安曲線上某點處的斜率)。這裡我們再花一個小節詳細解釋一下,為什麼不用簡單明瞭的普通電阻(即直流電阻)概念,還要專門去發明抽象的“交流電阻”這一 ...
1. 交流分析與交流電阻
我們曾經在 1-4二極體的電阻 大致講過交流電阻的特性,交流電阻並不是一個實際的可直接測量的物理量,而是一個抽象的量(是伏安曲線上某點處的斜率)。這裡我們再花一個小節詳細解釋一下,為什麼不用簡單明瞭的普通電阻(即直流電阻)概念,還要專門去發明抽象的“交流電阻”這一概念?
首先我們必須明確一點,一樣東西被髮明出來,肯定不是為了折騰自己,讓事情複雜化,而是要使解決問題變得更簡單。其實,用交流電阻來分析電路中的小信號情況比只用直流電阻要更加直觀和簡單,下麵我們通過一個例子詳細說明這一點。
由於在模擬電路中,很多都是非線性的伏安關係曲線,而且大多沒有太精確的數學表達式,故只能用圖解法去近似求解。比如在下圖中,給你一個非線性器件的伏安曲線,然後指定一個輸入電壓v1,讓你求對應的輸出電流i1,你怎麼求?
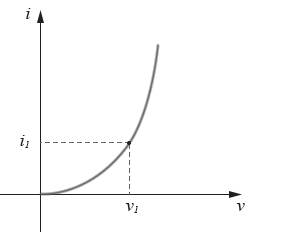
圖4-2.01
答案是沒什麼太好的辦法,只能在圖上用尺子量。假若再指定v2、v3、……,讓你求對應的i2、i3、……,怎麼求?答案同樣是沒什麼快捷方法,還是只能一次次在圖上量,很麻煩。
好,就算這個還能勉強從圖上量出來。下麵再假設,輸入電壓不是恆定值,而是一個變化量,比如正弦電壓,表達式為:v(t)=sin(t),讓你求對應的電流表達式i(t),怎麼求?
如果是個線性電阻,電流表達式很好求,電流=電壓 / 電阻:i(t)=v(t)/R = sin(t)/R
但如果是非線性器件,就完全沒辦法了。(當然,也不是徹底沒辦法,可以在圖上畫很多點,然後量出一系列的i-v對應點,再用曲線耦合的方法去估一個多項式表達式,非常麻煩)。
好,那現在問題變一下,假設我們在器件上施加一個如下圖所示的含直流分量和小信號正弦分量的電壓:v(t) = VQ + a*sin(t),(其中,VQ為其直流分量,a為正弦信號的幅值,且VQ遠大於a),
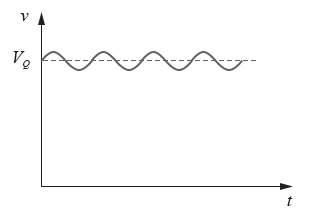
圖4-2.02
讓你求對應的電流表達式i(t),請問可不可以?答案是可以的,分析思路如下:
• a. 首先,我們可以利用作圖法或其他分析方法(如上一章的各種BJT直流分析算式),算出輸入電壓的直流分量VQ對應的電流直流分量IQ,如下圖所示:

圖4-2.03
其中,RQ = VQ/IQ 就是Q點的直流電阻。
• b. 然後我們觀察電壓信號在非線性伏安曲線上的變化範圍:
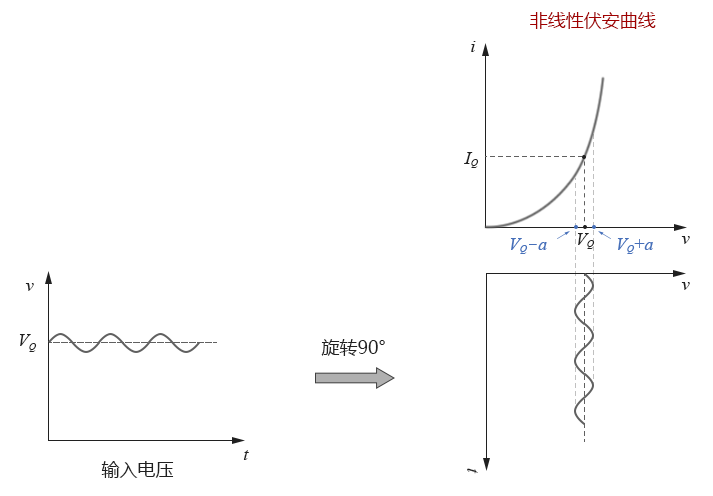
圖4-2.04
可以看到,輸入電壓v只在VQ點上下一個很小範圍內波動,在如此小的一塊範圍內,我們可以把伏安曲線近似視為直線,如下圖所示:
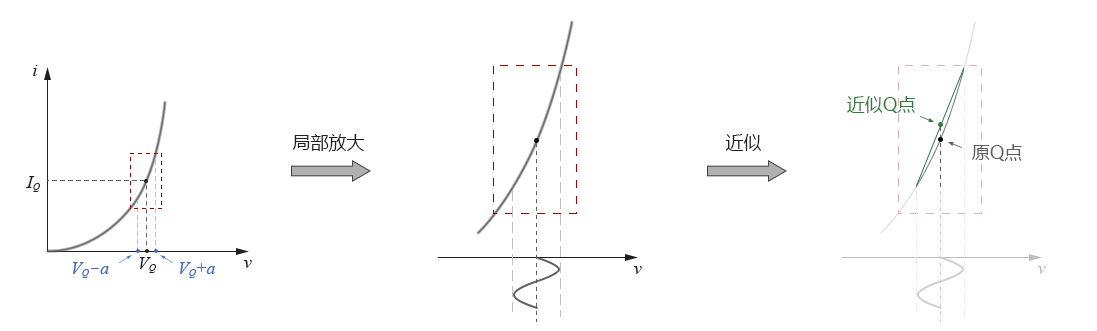
圖4-2.05
• c. 假設近似直線的斜率為k,我們可以很容易地寫出在這個小範圍內的任意一點vx的i-v對應關係式,見下圖所示:
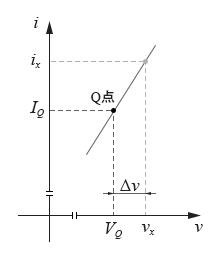
圖4-2.06
上圖中,電流i的表達式為:
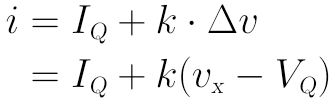
寫出上式後,vx為任意的表達式都可以很方便地表示出電流i,就拿我們上面給出的v(t) = VQ + a*sin(t)來說,將v(t)作為vx代入上式,可求得:

如果把輸入電壓v(t)寫成直流分量加交流分量的表示形式:
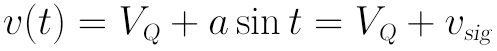
(上式中,vsig表示交流分量,由於交流分量總是隨時間變化的,故省略“(t)”也不影響含義的表達,而且更簡潔)
那麼,對應電流 i 就可以寫成:
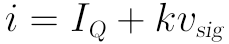
• d. 最後的問題就是,斜率k怎麼求。我們再回來看那個局部放大圖:
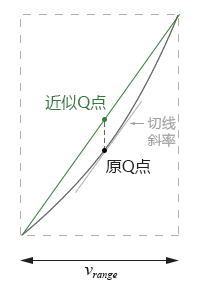
圖4-1.07
如果vrange的範圍足夠小,根據高數中的微分中值定理(也叫拉格朗日公式、有限增量公式),那麼可以用原曲線Q點處的切線斜率(即曲線在原Q點處的導數)作為近似直線的斜率。這個斜率就是Q點處的交流電導gsig,交流電導的倒數即為交流電阻rsig:
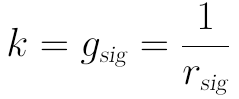
所以,交流電阻的來源是原非線性曲線在Q點處的斜率,這是一個抽象的量,且曲線在各個不同位置的斜率並不相同,故不同的Q點有不同的交流電阻。
然後再把這個交流電阻rsig代入上面的輸出電流i表達式:
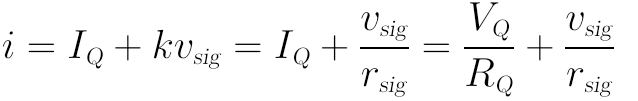
可以看到,在對應電流i的表達式中,直流和交流完全可以隔離表達(直流分量與直流電阻運算、交流分量與交流分量運算),如此就可大大簡化計算。一般可以從廠商給出的BJT數據規格書中查到所需的交流電阻。
2. 輸入電阻與輸出電阻
輸入輸出電阻這個概念,對於放大器來講非常重要,尤其在多級放大器中,這是一個非常重要的設計指標。遺憾的是,很多模電教材上都對此概念都不詳細講,直接預設讀者已經掌握了這一基礎概念;但先導的電路原理課程,很多時候也不會專門去講這個概念。因此會導致初學者在學習模擬電路的時候產生困惑,這裡我們將其作為交流分析的前置基礎知識,單獨講一個小節,以闡明其基本原理。
(1)非理想電源
對於理想電壓源來說,並不存在輸入/輸出電阻這一問題,理想電壓源對於任何負載,其輸出都是一個恆定的電壓值。但是,現實中所有的電源都是非理想的,都會有一個內阻的存在,如下圖所示:
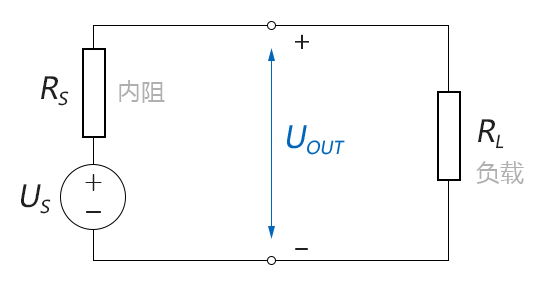
圖4-2.08
圖中,由於內阻RS的存在,使得非理想電壓源的輸出電壓UOUT會受負載RL的影響很大。舉例來說:在US=5V,RS=1Ω的情況下,若負載RL=100Ω,輸出電壓UOUT為:
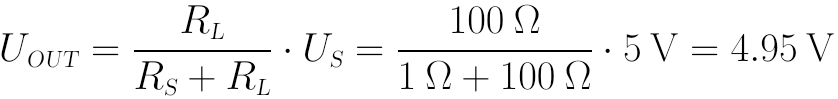
看上去似乎沒什麼大問題。但是,若負載RL=1Ω時,輸出電壓UOUT即變為:

電壓源的輸出電壓UOUT只有原來的一半左右,效率非常低。若是負載為RL=0.1Ω,輸出電壓UOUT只有0.45V,完全沒法用。
因此,我們可以看出其中的一些應用規律:
對於電源來說,內阻的阻值越小越好。比如:若內阻RS只有0.001Ω,即便負載RL=0.1Ω時,也能輸出約4.95V。
而對於負載來說,負載的阻值越大越好。比如,若負載阻值為RL=10kΩ時,即便內阻RS為100Ω也沒太大問題。
(2)輸入電阻
我們將這個規律放到放到具體放大器中來看。下圖是一個簡單的分壓偏置共射放大器:
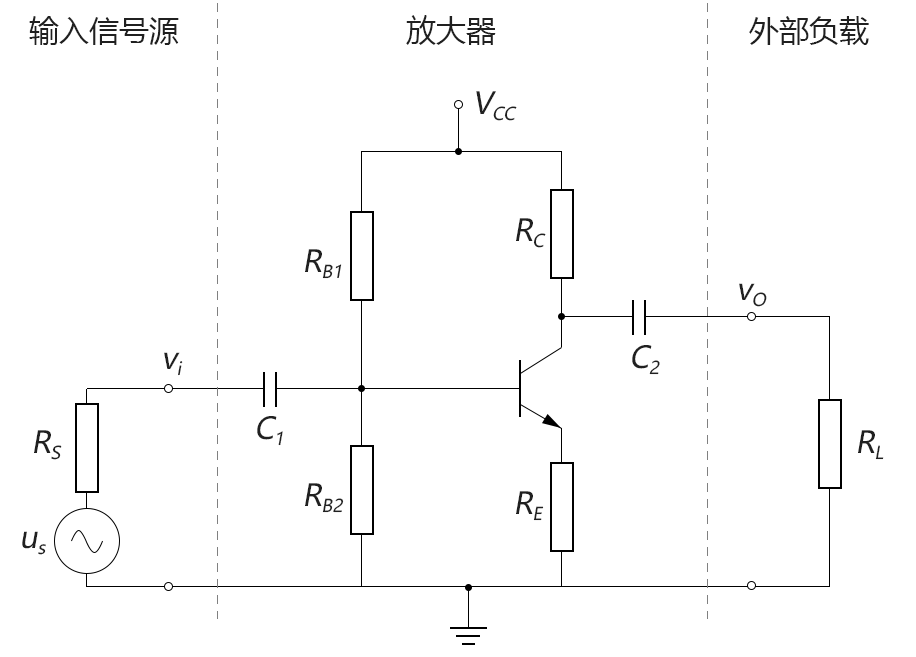
圖4-2.09
上圖分為三個部分,我們從左到右一點點看。
對於“輸入信號源”和“放大器”來說,“輸入信號源”就相當於一個非理想電源,“放大器”的輸入端就相當於負載(電容C1和C2在這裡對於交流信號可視為短路),如下圖所示:
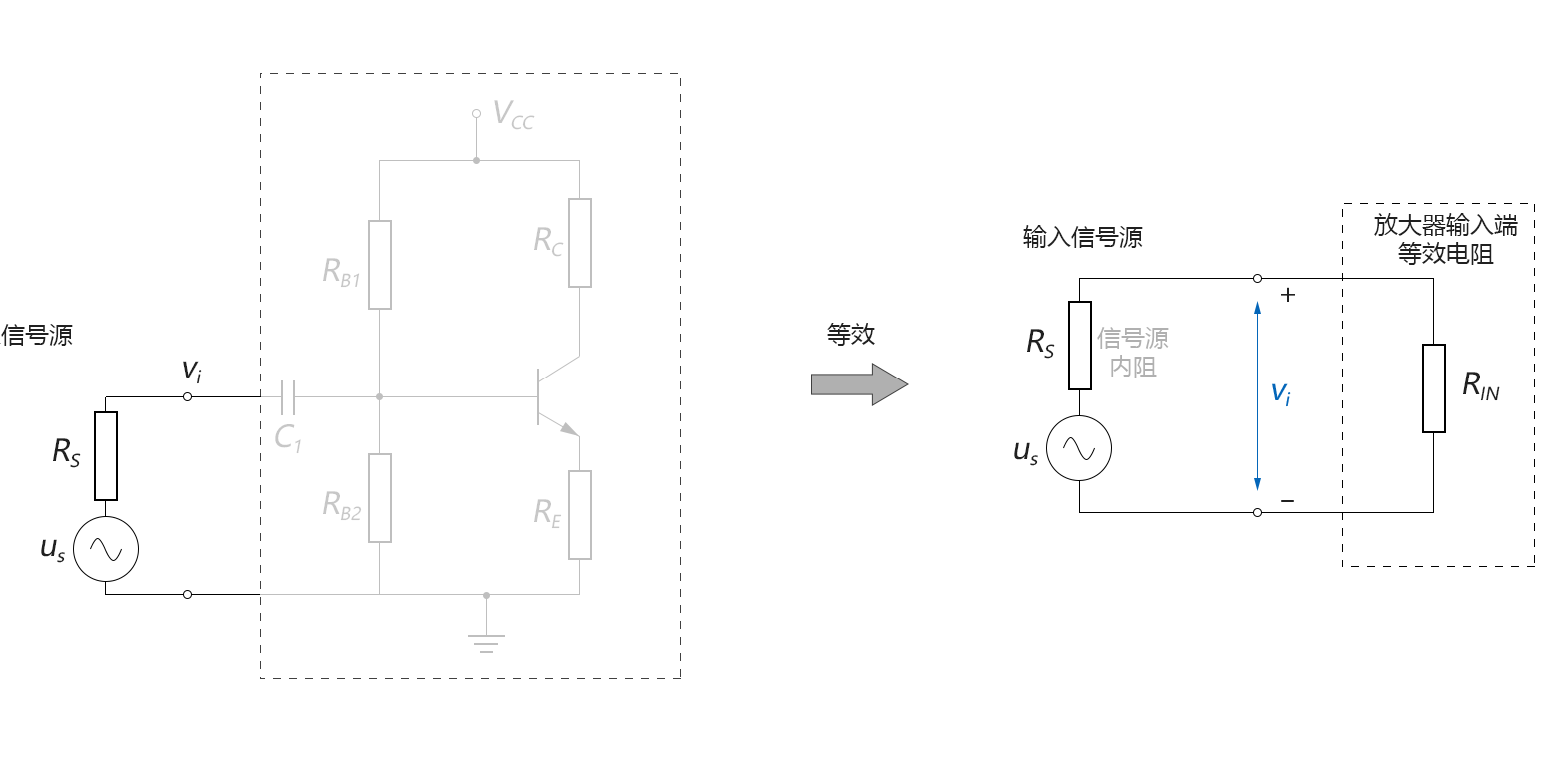
圖4-2.10
輸入信號源的內阻受條件限制一般為固定值,那為了使輸入信號電壓us能儘可能多地能載入到放大器上,而不是消耗在信號源的內阻上,我們就要使放大器的輸入端的等效負載電阻儘可能地大。
由於這個等效負載電阻是從信號源的角度向放大器的輸入端看入的,故我們一般把這個等效負載電阻稱為:放大器的輸入電阻RIN。這也就是為什麼人們常常會簡要地說,輸入電阻越大越好。
(3)輸出電阻
我們再看右邊2個部分,對於“放大器”和“外部負載”來說,“放大器”就相當於非理想電源,“外部負載”就相當於負載,如下圖所示:
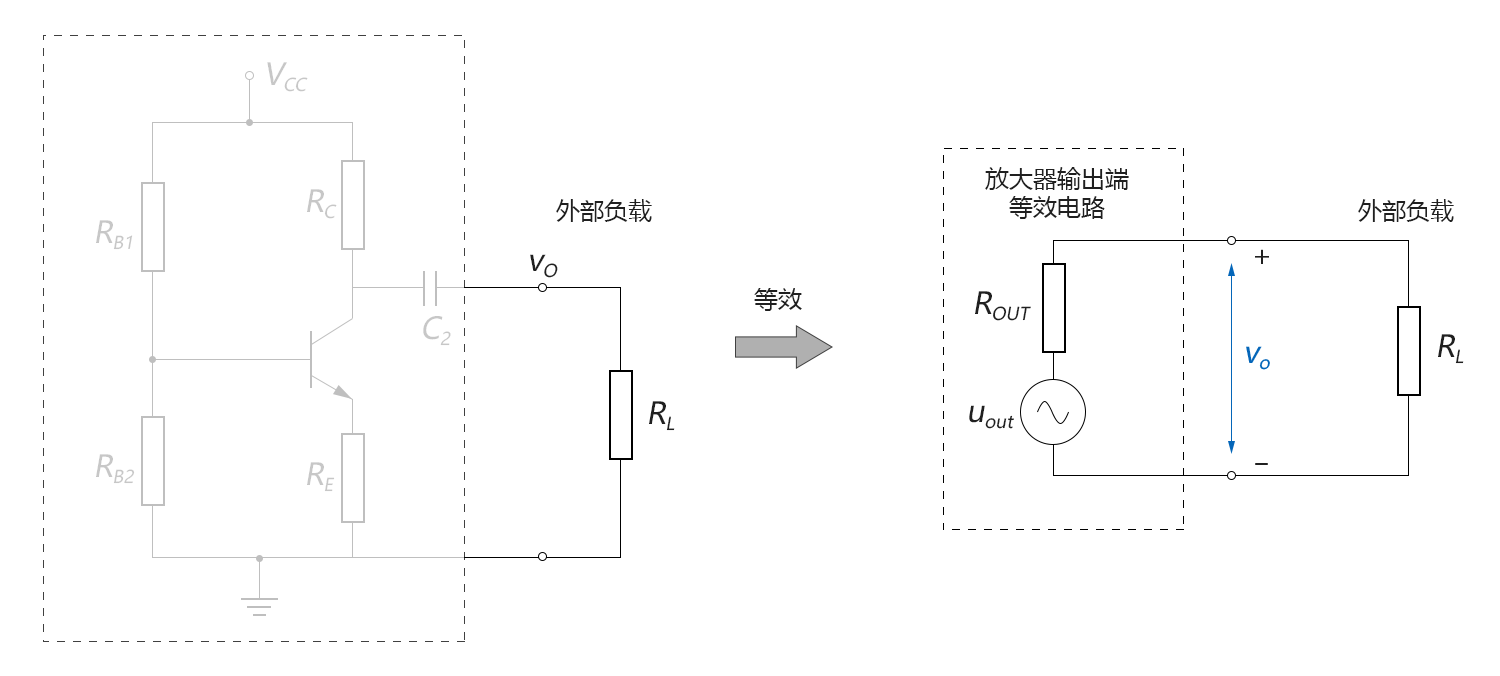
圖4-2.11
由於外部負載的阻值為固定值,那麼為了使放大器的輸出信號能儘可能多地載入到外部負載上,而不是消耗在放大器內部,我們就要使放大器輸出端的內阻儘可能地小。
由於這個內阻是從外部負載的角度向放大器的輸出端看入的,故我們一般把這個電阻稱為:放大器的輸出電阻ROUT。這也就是為什麼人們常常會簡要地說,輸出電阻越小越好。
(4)交流輸入輸出電阻
上面為闡釋概念方便,我們在放大器的輸入端和輸出端,只等效了交流部分。更嚴格來講,放大器的輸入端和輸出端其實都同時包含直流分量和交流分量。一個同時包含直流分量和交流分量的非理想電源如下圖所示:
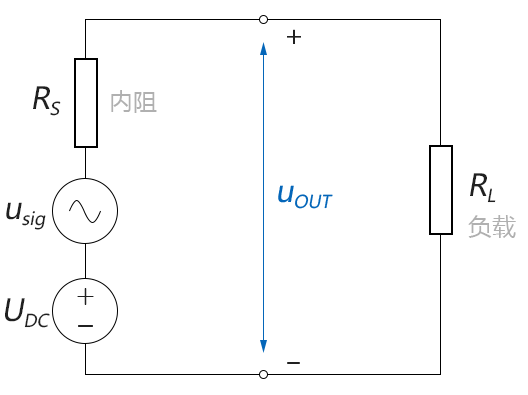
圖4-2.12
圖中,信號源為一個含有直流分量UDC和交流分量usig的混合源,內阻為RS。對於普通的線性電阻負載RL,其輸出電壓uOUT的表達式為:
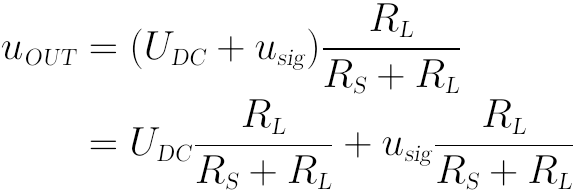
從上式可見,輸出電壓uOUT也可以分為直流部分和交流部分,而且可從信號源的直流部分UDC和交流部分usig分別算得。這是當負載和電源內阻都為普通的線性電阻時分析情況,比較簡單。
而由於放大器一般採用BJT晶體管或FET場效應管,都是非線性器件,所以放大器的輸入端的輸入電阻並不能簡單等效為一個線性電阻RIN,而是要等效成一個非線性器件。同樣的,放大器的輸出端的輸出電阻(即輸出等效電路中的內阻),也不能簡單等效為一個線性的電阻ROUT,也是要等效成一個非線性器件。
但是,正如我們前面在“交流電阻”小節分析的那樣,對於非線性器件,如果源輸入信號是一個典型的“直流分量疊加一個小信號交流分量”的信號,那麼其分析方法就可以大大簡化:可以將直流部分和交流部分分開計算,最後再把得到的結果疊加起來就可以了。因此,放大器的輸入端和輸出端計算可以分別作如下等效分離:
● 輸入端直流交流等效分離:
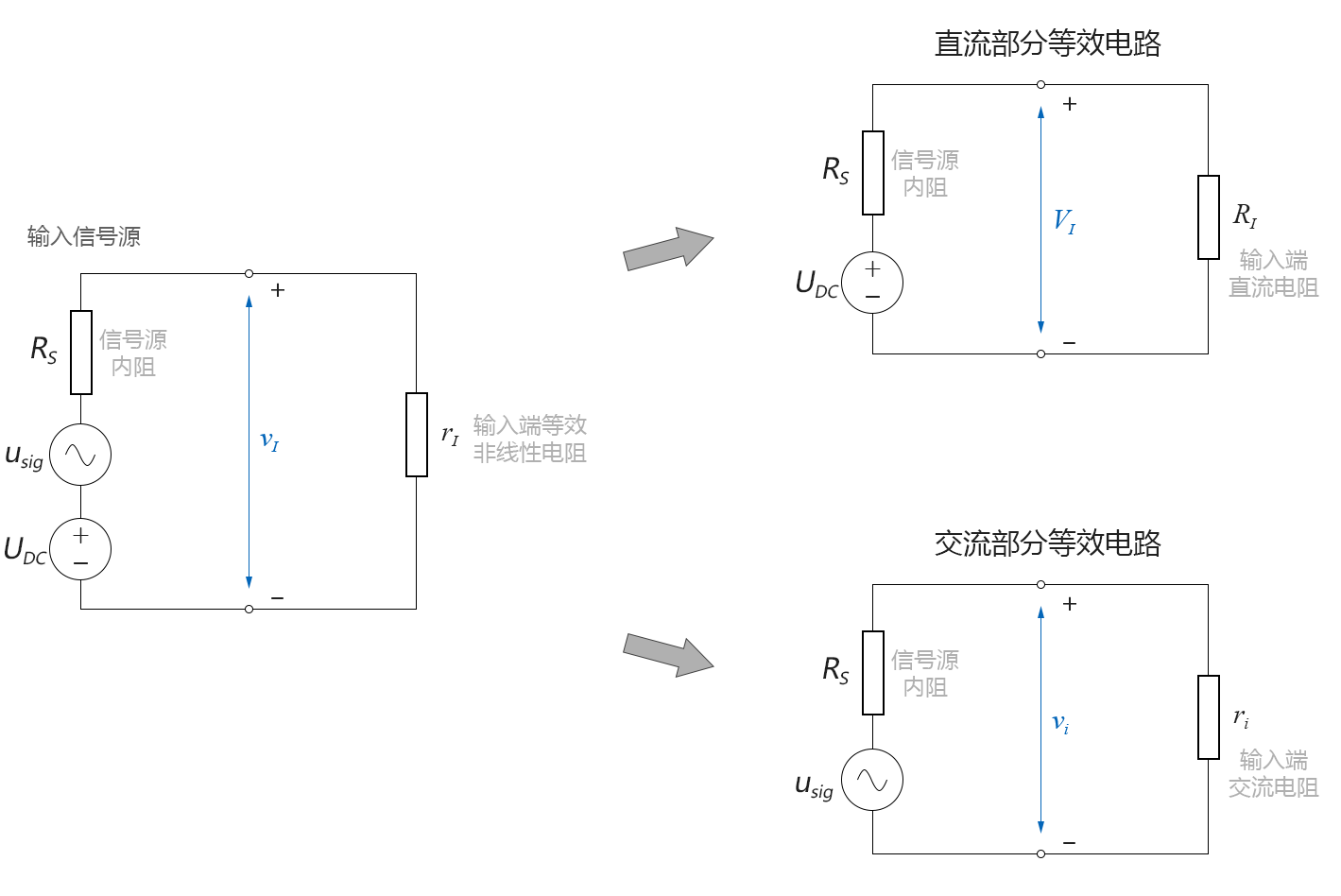
圖4-2.13
直流部分的輸入電壓VI為:
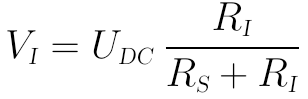
交流部分的輸出電壓vi為:

總輸出電壓vI為:
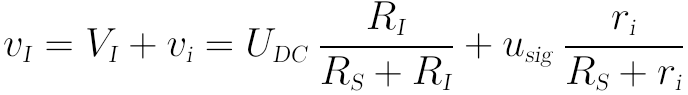
在這裡我們通常將信號源的內阻看成是一個普通的線性電阻。對於普通的線性電阻,其直流電阻和交流電阻是完全相同的,因此RS在直流部分和交流部分的表達式中也是一致的。
● 輸出端直流交流等效分離:
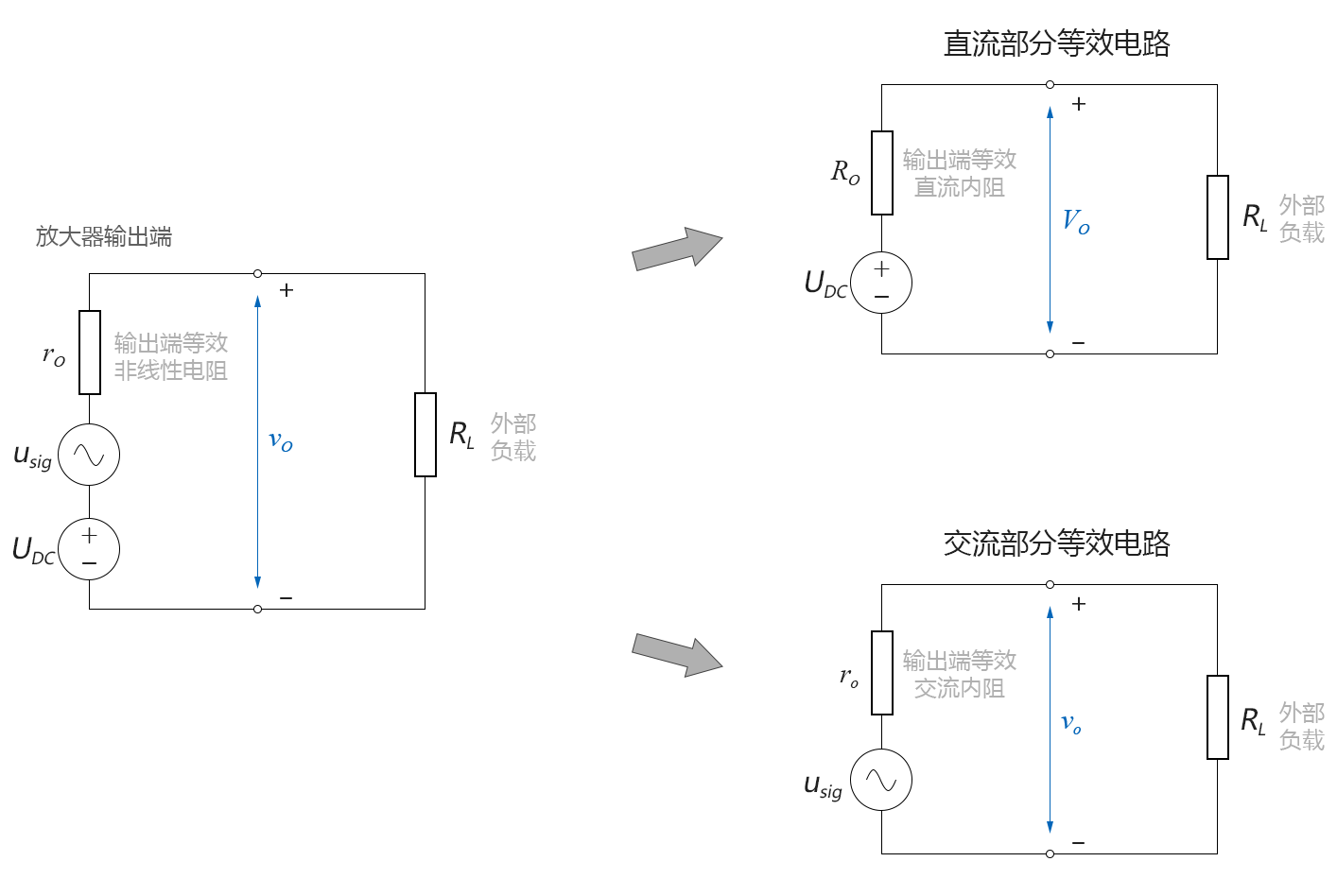
圖4-2.14
這裡放大器的輸出端相當於信號源,其內阻是非線性的,所以內阻也要做直流和交流的分離,如上圖所示。最終的輸出電壓表達式為:
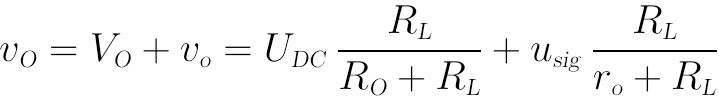
( end of 4-2)


