初級模擬電路：3-6 共射放大電路-2（分壓偏置的直流分析）

回到目錄

（續上小節）

3. 分壓偏置

      前面的“改進型固定偏置”電路，雖然情況比原始的固定偏置電路好了一點，但還是不太理想，於是人們又設計出了性能更加穩定的分壓偏置（voltage-divider bias configuration）電路，如下圖所示：

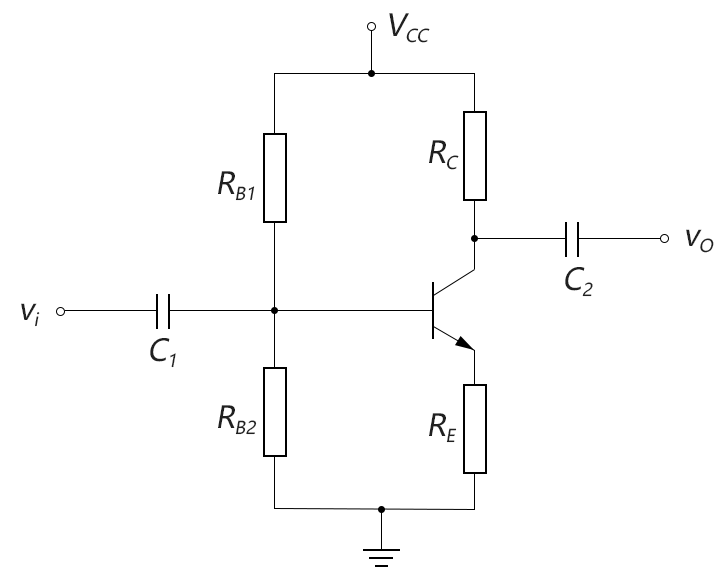
圖3-6.06 

      分壓偏置電路的穩定性非常完美，放大繫數β的變化對輸出靜態工作點I_C和V_CE幾乎沒有什麼影響，我們在下麵的分析中可以驗證這一點。

      對於分壓偏置的輸入端分析，有“近似分析”和“精確分析”兩種方法，一般在實際工程應用中，“近似分析”法基本就夠用了，但是“精確分析”法你也是需要掌握的。對於學習來說，仔細揣摩和比較這兩種方法，可以增強你對模擬電路關於什麼時候可以作簡化的直覺。

（1） 近似分析法

● 輸入靜態工作點：

      我們將分壓偏置的共射放大電路重畫於下，在直流分析（靜態分析）時，可將動態輸入電壓v_i視為0。

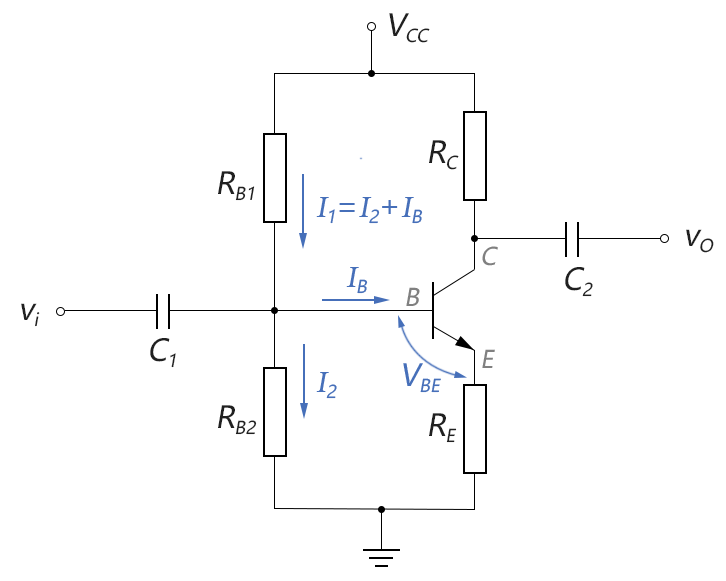
圖3-6.07 

      上圖中，由於I_B為微安級，而I₁和I₂都為毫安級，因此，可以近似認為：I₁≈I₂。

      作瞭如上近似後，基極B點的電壓V_B就很好算了，就是R_B1和R_B2對V_CC的分壓：

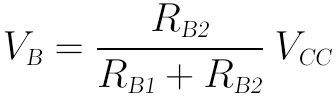
      而E點電壓V_E即為：

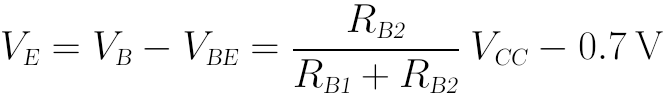
      至於I_B，由於我們剛纔已經將I_B近似為0了，故這裡I_B就無法再計算了。好在近似分析法中，即使我們不計算I_B，也不影響後面的“輸出靜態工作點”的計算。

● 輸出靜態工作點：

      由於在近似分析法中，I_B已經近似為0，就不能用I_C=β I_B這個公式來計算I_C了。我們需要用別的方法來計算I_C，看下圖：

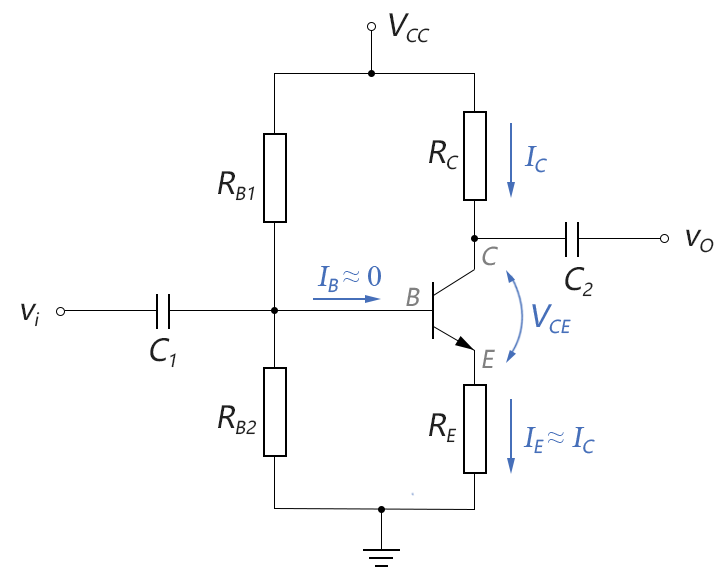
圖3-6.08 

      在剛纔的輸入分析中，我們已經算得V_E：

      而I_E即為：

      我們再近似認為：I_C≈I_E，即可得到：

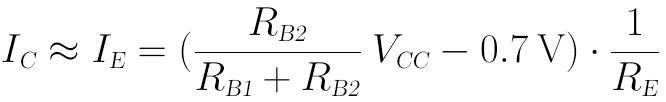
      然後V_CE即為：

（2） 精確分析法

      在精確分析法中，不再將I_B近似為0，而是列出詳盡的迴路方程，然後進行數值解，如下圖所示：（V_BE仍簡化為0.7V）

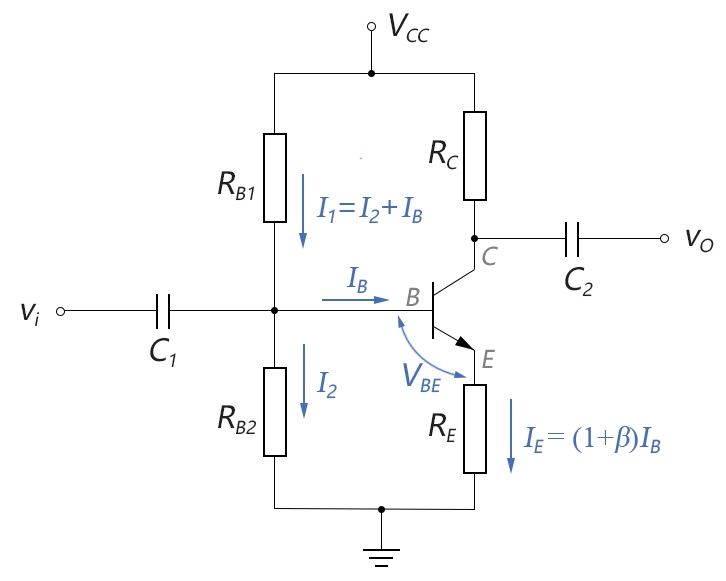
圖3-6.09 

      對於上面的電路圖，我們可以列出若幹方程硬算，也可以藉助一些電路等效化簡方法巧妙地減少手算工作量，兩者結果是一樣的。下麵分別予以介紹：

● 硬核計算：

      對於上圖，主要的電流關係式和主要的電壓關係式為：

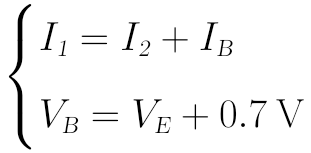
      我們可以分別列出I₁、I₂、V_E的歐姆定律計算式：

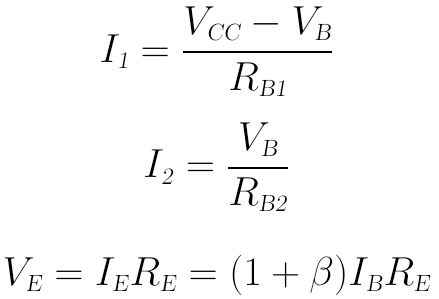
      將它們代入上面的主電流、電壓關係式可得：

      在上面這個方程組中，僅含有V_B和I_B兩個未知變數。耐心一點、按部就班地一步步推算，是可以解出I_B和V_B的，I_B最終可解得為：

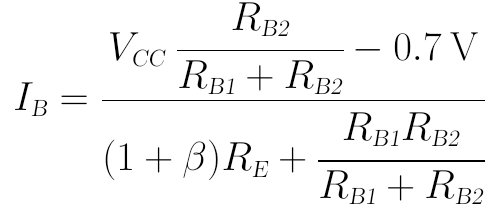
      解出I_B後，用I_C=β I_B的關係式，可以很方便地求出輸出端的靜態工作點I_C和V_CE，這裡就不再重覆寫了。

● 電路等效化簡後計算：

      上面的方程組，看上去好像不算太複雜，但其實真的算起來，還是有一點工作量的（至少我用了三大張紙）。而且在解方程時把各個量顛來倒去地抄寫，很容易出錯。所以，一般在做電路計算時，會先考慮一下電路能不能化簡，把電路儘量化簡成等效的最簡單形式，這樣最終列出的方程就會比較簡單，解起來也不太會出錯。

      電路等效化簡最常用的方法就是：戴維南等效電路和諾頓等效電路，我們現在嘗試用戴維南等效電路的方法，對上面的圖3-6.09進行等效化簡：

      對於輸入端的分析，從三極體的基極（B點）向左看，可以將B點左側的外部電路視為一個戴維南等效電路，如下圖所示：

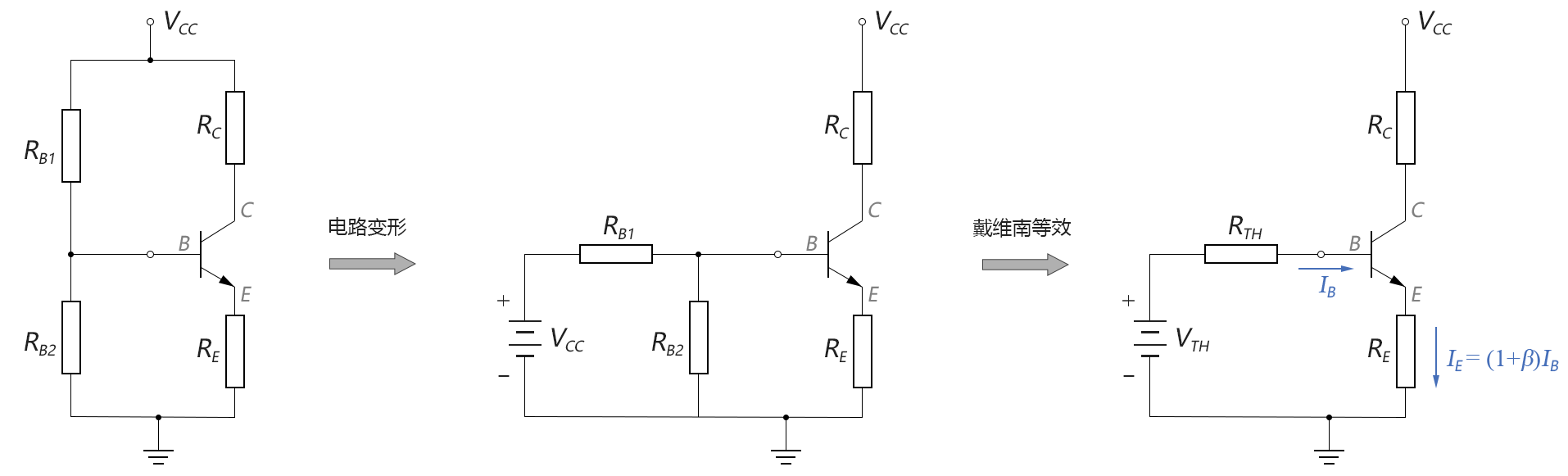
圖3-6.10 

      對於上面做完戴維南等效的最右圖，列寫輸入側的KVL方程就很容易了：

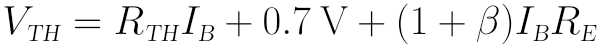
      解得I_B為：

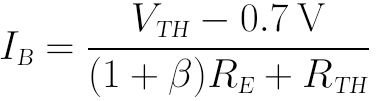
      是不是要比上面的硬核計演算法要簡單很多？至於戴維南等效電壓V_TH和戴維南等效電阻R_TH就很好算啦，如下圖所示：

圖3-6.11 

      計算戴維南等效電壓V_TH時，可將右側視為開路：

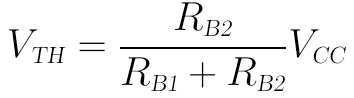
      計算戴維南等效電阻R_TH時，可將電壓源V_CC視為短路：

      然後再將V_TH和R_TH代入上面的I_B，最終結果和前面硬算的結果是一致的。

案例3-6-2：分別用近似分析法和精確分析法，計算下圖分壓偏置電路的I_B, I_C, V_CE。

圖3-6.a2 

解：（1）近似分析法：

      驗證：V_CE > V_CEsat，說明BJT工作於放大區的假設正確。

（2）精確分析法：

      先計算戴維南等效電壓和電阻：

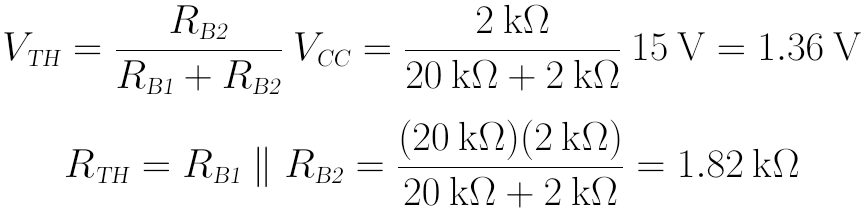
      再將其代入I_B計算式：

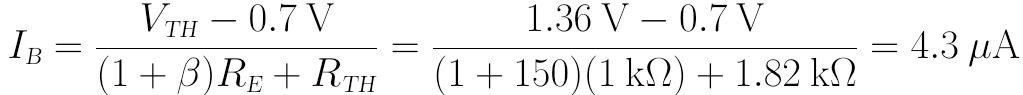
      假設BJT工作於放大區：

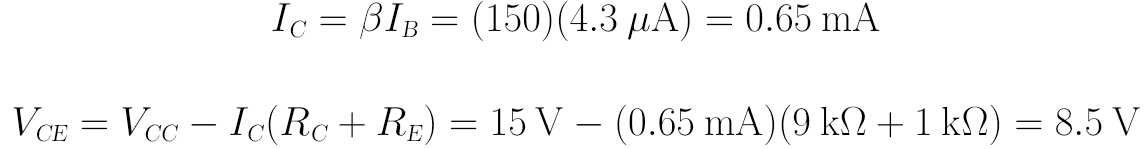
      驗證：V_CE > V_CEsat，說明BJT工作於放大區的假設正確。

      比較：從上面兩種方法計算得到的I_C和V_CE來看，兩種演算法的結果非常接近，故知近似分析法在大部分情況下是可以對電路進行大致評估計算的，而且近似分析法不需要用到β參數，說明分壓偏置電路的靜態工作點基本不受β影響。

（3） 飽和條件

      當V_CE<V_CEsat時，晶體管進入飽和區。因此，我們可以算出此時的集電極飽和電流I_Csat，

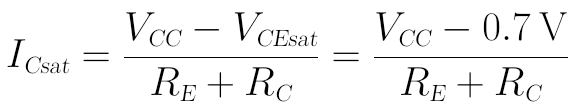
      當I_C>I_Csat時，晶體管進入飽和。

回到目錄

（ end of 3-6-2）