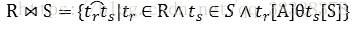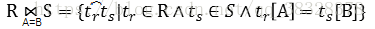關係型資料庫-關係操作集合 1、 基本的關係操作 關係模型中常用的關係操作包括查詢(Query)操作和插入(Insert)、刪除 (Delete)、修改(Update)操作兩大部分。 查詢操作分為:選擇、投影、連接、除、並、差、交、笛卡爾積等; 五種基本操作:選擇、投影、並、差、笛卡爾積; 關係操作 ...
關係型資料庫-關係操作集合
1、 基本的關係操作
關係模型中常用的關係操作包括查詢(Query)操作和插入(Insert)、刪除 (Delete)、修改(Update)操作兩大部分。
查詢操作分為:選擇、投影、連接、除、並、差、交、笛卡爾積等;
五種基本操作:選擇、投影、並、差、笛卡爾積;
關係操作的特點是集合操作方式,即操作的對象和結果都是集合、這種操作方式也稱為一次一集合的方式。
2、關係數據語言的分類
關係操作是通過關係語言來實現的。 關係語言的特點是高度非過程化,即:
(1)用戶不必請求資料庫管理員為其建立特殊的存取路徑,存取路徑的選擇由 DBMS 的優化機制來完成;
(2)用戶也不必求助於迴圈和遞歸來完成數據的重覆操作。
關係操作的能力可以用兩種方式來表示:代數方式和邏輯方式。 關係代數、元組關係演算和域關係演算均是抽象的查詢語言。結構化查詢語言SQL充分體現了關係數據語言的特點和優點,是關於資料庫的標準語言。
關係數據語言可以分為三類:關係代數語言、關係演算語言以及兼具兩者雙重特點的語言。三類語言的共同特點是語言具有完備的表達能力,是非過程化的集合操作語言,功能強,能夠獨立使用也可以嵌入高級語言中使用。
3、 關係代數
操作包含三大要素:操作對象、操作符、操作結果。在關係代數操作中,操作對象和操作結果均為關係。 關係代數直接應用關係的運算來表達操作目的,而代數用到的運算符包括集合運算符合專門的關係運算符兩類,如下表所示:
(關係代數運算符)
A. 傳統的集合運算是二目運算,關係看成元組的集合,其運算關係是從關係的“水平”方向,即行的角度來進行,有並、差、交、笛卡爾積 4 種運算。
1. 並:假設有兩個關係 R1 和 R2,R1 和 R2 的並運算產生一個新關係 R3。R3 是 由屬於關係 R1 或 R2 的所有不同元組所組成,記為 R3=R1∪R2。
2. 差:假設有兩個關係 R1 和 R2,R1 和 R2 的差運算產生一個新關係 R3。R3 是由屬於關係關係 R1,但不屬於 R2 的元組組成,記為 R3=R1-R2。
3. 交:假設有兩個關係 R1 和 R2,R1 和 R2 的交運算產生一個新關係 R3。R3 是由既屬於關係 R1,同時又屬於 R2 的元組組成,記為 R3=R1∩R2。
4. 笛卡爾積:假設有兩個關係 R1 和 R2,且 R1 為 m 元關係,R2 為 n 元關係, R1 和 R2 的笛卡爾積產生一個新關係 R3,記作 R3=R1✖R2。R3 是 由 R1 和 R2 的所有元組連接而成的具有(m+n)個分量的元組組成。
B. 從列的角度,可分為一元專門關係操作和二元專門關係操作。 一元專門關係操作包括對單個關係進行垂直分解的投影運算和進行水平分解選擇運算;二元專門關係操作則是對兩個關係進行操作,包括連接運算和除運算。
(0)相關概念:
(0.0)域是一組具有相同數據類型值的集合。
(0.1)設關係模式為R(A1, A2, …, An)。它的一個關係設為R。t∈R表示t是R的一個元組。t[Ai]則表示元組t中相應於屬性Ai的一個分量 。
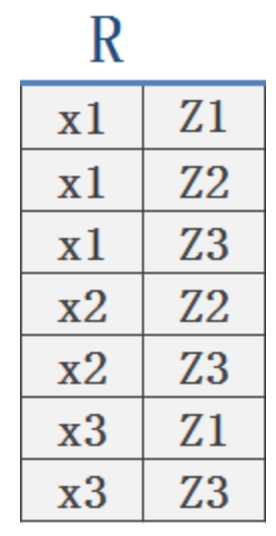
(0.2)給定一個關係R(X,Z),X和Z為屬性組。我們定義,當t[X]=x時,x在R中的象集(Images Set)為:
eg:如下圖所示關係R,則
x1在R中的像集Z(x1)={Z1,Z2,Z3},
x2在R中的像集Z(x2)={Z2,Z3},
x3在R中的像集Z(x3)={Z1,Z3}。
註:以下舉例統一使用,設存在Student表,Sno表示學號屬性,Sage表示年齡,Sname表示姓名,Ssex表示性別,Sdept表示所在系
(1) 選擇(SELECT)
選擇運算表示為: ![]()
其中,F 為條件表達式,R 為指定的被運算關係名。
sql偽代碼形式如下:
SELECT 關係名 WHERE 條件
eg:
則查詢表中年齡小於20的學生,
關係代數方式:
SQL方式: select * from Student where Sage > 20 (2) 投影(PROJECTION)
關係R上的投影是從R中選擇出若幹屬性列組成新的關係。記作:![]() 其中A為R中的屬性列。投影操作是從列的角度進行運算。
其中A為R中的屬性列。投影操作是從列的角度進行運算。
eg:
查詢學生的姓名和所在系,即求Student關係上學生姓名和所在系兩個屬性上的投影
關係代數方式: ∏Sname,Sdept(Student)
SQL方式: select Student.Sname,Student.Sdept form Student
註意:投影之後不僅取消了原關係的某些列,而且還可能取消某些元祖,因為取消了某些屬性之後,就可能出現重覆行,應取消這些完全相同的行。
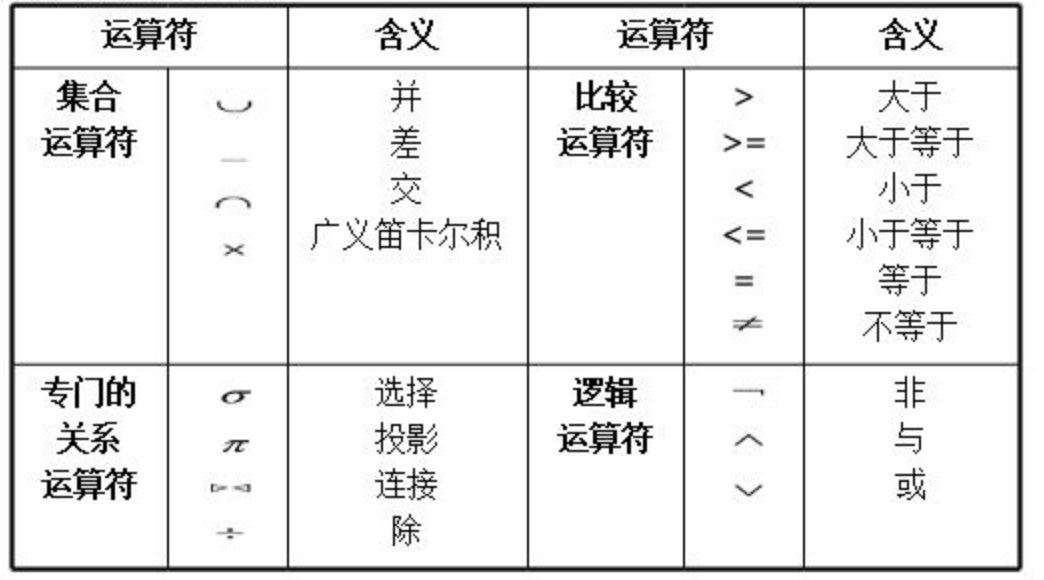
(3) 連接(JOIN)
連接運算也稱為θ連接,從兩個關係(R、S)中的廣義笛卡爾積中選取屬性間滿足一定條件的元組形成一個新的連接:
其中: A為包含R中的屬性的表達式;
B為包含S中的屬性的表達式;
θ通常為關係比較符。
(3.1) 非等值連接
θ不為“=”的連接稱為非等值連接
sql偽代碼: select * from emp e join dept d on e.sal > d.avgsal
(3.2) 等值連接
θ為“=”的連接稱為等值連接,它是從關係R和S的笛卡兒積中選取A、B屬性值相等的那些元組。等值連接的屬性名可以相同也可以不相同。
select * from emp e join dept d on e.sal = d.avgsal
select * from emp e join dept d on e.deptno = d.deptno
(3.3) 自然連接
自然連接是一種特殊的等值連接,它要求兩個關係進行比較的分量必須是同名的屬性組,並且在結果中把重覆的屬性列去掉。一般的連接是從行的角度進行操作,自然連接需要取消重覆列,所以它是從行和列的角度進行操作。
select * from emp natural join dept
(3.4) 外連接
兩個關係R和S在做自然連接時,選擇兩個關係在公共屬性上值相等的元組構成新的關係。此時,關係R和S可能有在公共屬性上不相等的元組,從而造成R或S中元組的捨棄,這些捨棄的元組被稱為懸浮元組。如果把懸浮元組也保存在結果關係中,而在其他屬性上填空值,那麼這種連接就叫做外連接。
① 左外連接
如果只保留左邊關係R中的懸浮元組就叫做左外連接。
select * from emp e left join dept d on e.deptno = d.deptno --員工8888沒有部門,只保留左表的懸浮元組,其他屬性為null
② 右外連接
如果只保留右邊關係S中的懸浮元組就叫做右外連接。
select * from emp e right join dept d on e.deptno = d.deptno --40號部門沒有人,只保留右表的懸浮元組,其他屬性為null
③ 全外連接
如果保留兩邊關係R和S中的所有懸浮無級就叫做全外連接。
select * from emp e full join dept d on e.deptno = d.deptno --保留兩邊的懸浮元組,左表和右表各有一條懸浮元組記錄,一共16行
(3.5) 自連接
select * from emp e1 join emp e2 on e1.empno = e2.mgreg:
設圖中(a)和(b)分別是關係R和關係S,圖中(c)為非等值連接



(4) 除(DIVISION)
除運算表示為: R➗S,其中 R 和 S 代表兩個不同的關係。在除運算中,若被除關係為 m 元關係,除關係為 n 元關係,則運算結果為一個 m-n 元關係。
用象集來定義除法:
① 給定關係R(X,Y)和S(Y,Z),其中X、Y、Z為屬性組,R中的Y與S中的Y可以有不同的屬性名,但必須出自相同的域集;
② 元組在X上的分量值x的象集K要包含S在Y上投影的集合,滿足前麵條件的元組在X屬性上的投影就是R除以S的結果關係;
③ 除操作是同時從行和列角度進行的操作。
關係R
| X | Y |
| x1 | y1 |
| x1 | y1 |
| x1 | y2 |
| x2 | y3 |
| x2 | y5 |
關係S
| Y | Z |
| y1 | z1 |
| y3 | z2 |
R÷S
| X |
| x1 |
分析:
① S在(Y)上的投影的集合是:{(y1),(y3)};
② 元組在X上的分量值x的象集有兩組;
x1的象集K1={(y1),(y2),(y3)}
x2的象集K2={(y3),(y5)}
③ 從①②得知只有象集K1包含了S在(Y)上的投影;
④ 滿足以上條件的象集K1在X屬性上的投影為{(x1)}。
非常感謝您的閱讀,如需轉載請註明出處,本文鏈接https://www.cnblogs.com/huyangshu-fs/p/11624939.html
另附推薦相關博客鏈接https://blog.csdn.net/Alexshi5/article/details/80024250