貪心演算法之——黑白點的匹配（兩種實現方法）

一、題目

設平面上分佈著n個白點和n個黑點，每個點用一對坐標（x, y）表示。一個黑點b=（xb,yb）支配一個白點w=(xw, yw)當且僅當xb>=xw和yb>=yw。

若黑點b支配白點w，則黑點b和白點w可匹配（可形成一個匹配對）。

在一個黑點最多只能與一個白點匹配，一個白點最多只能與一個黑點匹配的前提下，求n個白點和n個黑點的最大匹配對數。

二、解題思路

　　一看完題目，一開始的思路是先將黑白點分別存入兩個數組中，再對兩個數組分別進行對x和對y的排序，在實際實驗過程中，發現排序完後數組的下標與點不好對應，這樣就不容易確定一個點是否已經匹配過。

　　經過瞭解查閱後發現了最大匹配問題的演算法，和本題類似，而且遞歸的操作複雜度遠小於多次對數組的排序。

　　而且過多的排序也造成了演算法思路難以理清。決定先學習掌握最大匹配度演算法再考慮本題…

　　在查閱了最大匹配度問題的思想後，發現這是一種遞歸形式的方法，演算法需要基於對二分圖的遍歷演算法，這就需要學習DFS或者BFS，所以又去複習了一下這兩個演算法，在徹底掌握了之後終於可以步入正題了…

（dfs和bfs的執行動態圖）

http://5b0988e595225.cdn.sohucs.com/images/20171101/f1f45fe9ca37425ba200180be89624b2.gif

http://5b0988e595225.cdn.sohucs.com/images/20171101/a85c0716fcc847f1915dddfcfd019c01.gif

理解了最大匹配演算法後，發現只要在圖遍歷的基礎上，多藉助一個matching數組，用來儲存各匹配點之間的聯繫，通過一些剪枝和判斷就可以實現。

我選擇了DFS進行最大匹配演算法的基礎演算法，DFS是對圖做出處理，在空間上需要藉助一張鄰接矩陣，我的想法是將黑白點問題化作圖，再根據題目的要求做出對應的鄰接矩陣，這樣再通過最大匹配就可以求解出來。

下麵主要針對這兩個問題討論並通過具體例子演示最大匹配核心思想。

1、如何將黑白點化作圖：

創建一個結構體

黑白點都看作頂點，只通過color進行區別

2、如何求對應鄰接矩陣：

       對儲存所有頂點的結構體數組做兩次迴圈，若滿足題目中黑點xy坐標大於白點，即將鄰接矩陣該位置置為1。

3、具體流程演示：

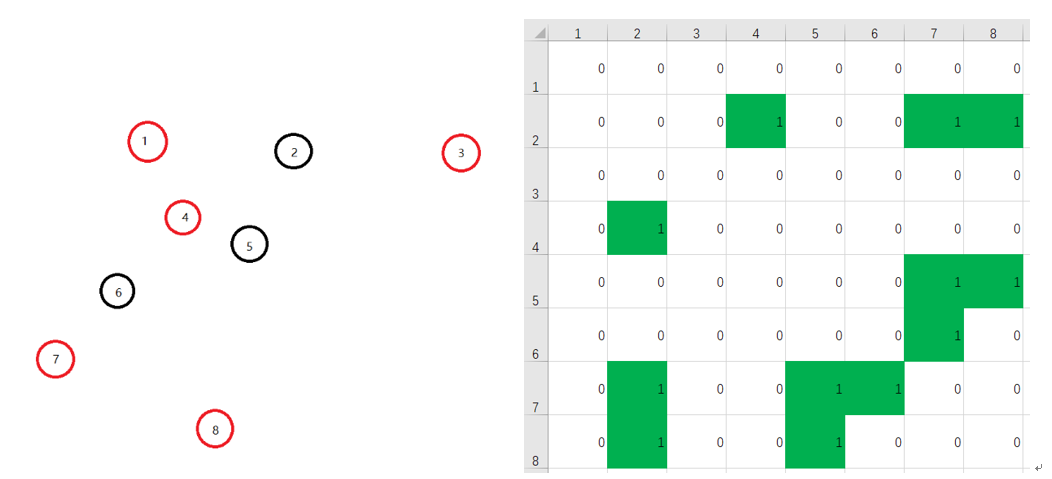
上圖分析：

通過鄰接表可以知道，2能控制4,7,8三點

一開始2就控制了4，跳過2點

接著5控制了7，跳過5點

6控制了7,但是7已經被5控制，這時回到5，

5控制了8，跳過5

這時7沒人控制，6控制7，流程結束，匹配度為3。

三、代碼（DFS BFS兩種實現方法）

  1 public class MaxMatching {// 基於DFS
  2 
  3     static int graph[][]; // 鄰接表 預設全為0
  4     static int n; // 節點數
  5     static int visit[]; // 是否訪問
  6     static int matched[]; // 是否已經匹配，對應的匹配點
  7     static vertex V[];//// 結構體數組儲存所有黑白
  8 
  9     public class vertex {// 頂點結構體
 10         public int color;// 白:0 黑：1
 11         public double Vx;
 12         public double Vy;
 13     }
 14 
 15     public void Init() {
 16         System.out.println("輸入的黑白點總數為：");
 17         Scanner sc = new Scanner(System.in);
 18         n = sc.nextInt();
 19         graph = new int[n][n]; // 鄰接表 預設全為0
 20         visit = new int[n]; // 是否訪問
 21         matched = new int[n]; // 是否已經匹配，對應的匹配點
 22         V = new vertex[n];
 23         InitGraph();// 初始鄰接矩陣
 24     }
 25 
 26     private void InitGraph() {
 27         Scanner sc = new Scanner(System.in);
 28         for (int i = 0; i < n; i++) {// 輸入黑白點
 29             V[i] = new vertex();
 30             System.out.println("please int color/x/y");
 31             V[i].color = sc.nextInt();
 32             V[i].Vx = sc.nextDouble();
 33             V[i].Vy = sc.nextDouble();
 34         }
 35         for (int i = 0; i < n; i++) {
 36             for (int j = 0; j < n; j++) {
 37                 if (i != j && (V[i].color == 1) && (V[j].color == 0) && (V[i].Vx > V[j].Vx) && (V[i].Vy > V[j].Vy)) {
 38                     graph[i][j] = 1;
 39                 }
 40             }
 41         }
 42     }
 43 
 44     // 顯示匹配結果
 45     public void show() {
 46         Arrays.fill(visit, 0);
 47         for (int i = 0; i < n; i++) {
 48             if (visit[i] == 0) {
 49                 if (matched[i] != -1) {
 50                     System.out.println("(" + V[i].Vx + "," + V[i].Vy + ")與" + "(" + V[matched[i]].Vx + ","
 51                             + V[matched[i]].Vy + ")" + "匹配");
 52                     visit[i] = 1;
 53                     visit[matched[i]] = 1;
 54                 }
 55             }
 56         }
 57     }
 58 
 59     /*
 60      * dfs實現, params: x:起始的未匹配點 return: 1:找到增廣路 0:未找到
 61      */
 62     public int dfs_solve(int x) {
 63         // 找到一個和節點存在邊的點，並且該點在本輪中沒有被訪問過
 64         for (int i = 0; i < n; i++) {
 65             if (graph[x][i] != 0 && visit[i] == 0) {
 66                 visit[i] = 1; // 標記為匹配過
 67                 // 按照交替路的模式找增廣路，增廣路相對於交替路的特性是就是，第一個節點和最後一個節點都是未匹配過的節點
 68                 if (matched[i] == -1 || dfs_solve(matched[i]) == 1) { // 直接跳到matched[i]能夠保證匹配邊和未匹配邊交替
 69                     // 說明找到了一個未匹配節點，將所有匹配邊變為未匹配邊，將所有未匹配邊變為匹配邊，這樣匹配邊數會加1,這個交換過程通過回溯實現
 70 
 71                     matched[x] = i;
 72                     matched[i] = x;
 73 
 74                     System.out
 75                             .println("(" + V[x].Vx + "," + V[x].Vy + ") 與 " + "(" + V[i].Vx + "," + V[i].Vy + ")" + "匹配");
 76                     return 1;
 77                 }
 78             }
 79         }
 80         return 0;
 81     }
 82 
 83     public void hungarian1() {
 84         Arrays.fill(matched, -1);
 85         int sum = 0;
 86         for (int i = 0; i < n; i++) {
 87             if (matched[i] == -1) {
 88                 System.out.println("從 " + "(" + V[i].Vx + "," + V[i].Vy + ")" + " 開始匹配");
 89                 Arrays.fill(visit, 0);// 重置瀏覽數組，用來瀏覽鄰接矩陣當前列
 90                 sum += dfs_solve(i);
 91             }
 92         }
 93         System.out.println("\n"+"最後共有 " + sum + " 匹配項");
 94         show();
 95     }
 96 
 97     public static void main(String[] args) {
 98         MaxMatching mm = new MaxMatching();
 99         mm.Init();
100         mm.hungarian1();
101     }
102 }