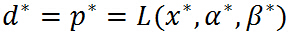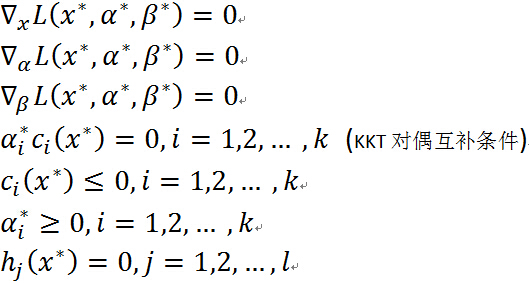轉載自https://www.cnblogs.com/90zeng/p/Lagrange_duality.html，本人覺得講的非常好！ 1.原始問題 假設是定義在上的連續可微函數（為什麼要求連續可微呢，後面再說，這裡不用多想），考慮約束最優化問題： 稱為約束最優化問題的原始問題。 現在如果不考慮約 ...
轉載自https://www.cnblogs.com/90zeng/p/Lagrange_duality.html，本人覺得講的非常好！
1.原始問題
假設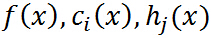
是定義在
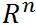上的連續可微函數（為什麼要求連續可微呢，後面再說，這裡不用多想），考慮約束最優化問題：
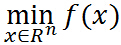
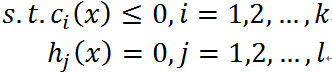
稱為約束最優化問題的原始問題。
現在如果不考慮約束條件，原始問題就是：
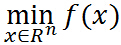
因為假設其連續可微，利用高中的知識，對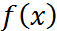
求導數，然後令導數為0，就可解出最優解，很easy. 那麼，問題來了（呵呵。。。），偏偏有約束條件，好煩啊，要是能想辦法把約束條件去掉就好了，bingo! 拉格朗日函數就是乾這個的。
引進廣義拉格朗日函數（generalized Lagrange function）:
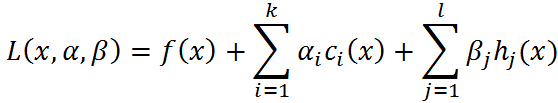
不要怕這個式子，也不要被拉格朗日這個高大上的名字給唬住了，讓我們慢慢剖析！這裡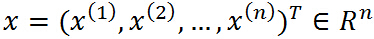
，
是拉格朗日乘子（名字高大上，其實就是上面函數中的參數而已），特別要求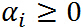
.
現在，如果把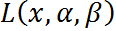
看作是關於的函數，要求其最大值，即
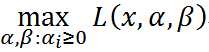
再次註意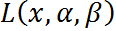是一個關於的函數，經過我們優化（不要管什麼方法），就是確定的值使得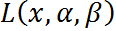取得最大值（此過程中把
看做常量），確定了的值，就可以得到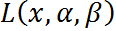的最大值，因為已經確定，顯然最大值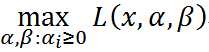就是只和有關的函數，定義這個函數為：
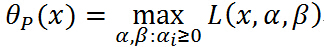
其中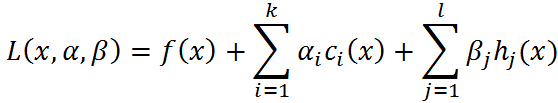
下麵通過是否滿足約束條件兩方面來分析這個函數:
- 考慮某個違反了原始的約束，即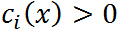
或者
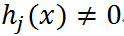，那麼：
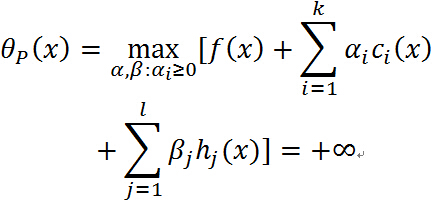
註意中間的最大化式子就是確定的之後的結果，若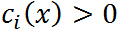，則令
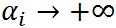，如果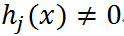，很容易取值
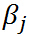使得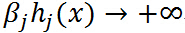
- 考慮滿足原始的約束，則：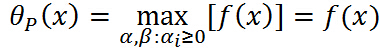
，註意中間的最大化是確定的過程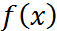，就是個常量，常量的最大值顯然是本身.
通過上面兩條分析可以得出：
那麼在滿足約束條件下：
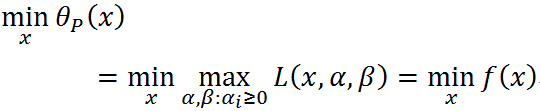
即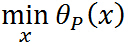
與原始優化問題等價,所以常用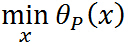代表原始問題，下標 P 表示原始問題，定義原始問題的最優值：
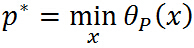
原始問題討論就到這裡，做一個總結：通過拉格朗日這位大神的辦法重新定義一個無約束問題（大家都喜歡無拘無束），這個無約束問題等價於原來的約束優化問題，從而將約束問題無約束化！
2.對偶問題
定義關於
的函數：
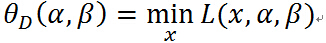
註意等式右邊是關於的函數的最小化，確定以後，最小值就只與有關，所以是一個關於的函數.
考慮極大化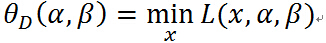，即
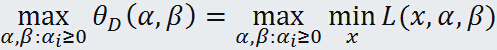
這就是原始問題的對偶問題，再把原始問題寫出來：
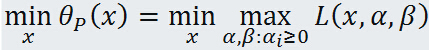
形式上可以看出很對稱，只不過原始問題是先固定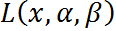中的，優化出參數，再優化最優，而對偶問題是先固定，優化出最優，然後再確定參數.
定義對偶問題的最優值：
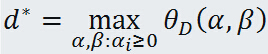
3. 原始問題與對偶問題的關係
定理：若原始問題與對偶問題都有最優值，則
證明：對任意的和，有
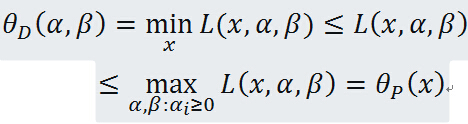
即
由於原始問題與對偶問題都有最優值，所以
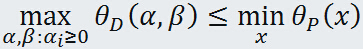
即
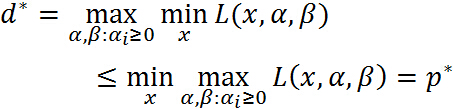
也就是說原始問題的最優值不小於對偶問題的最優值，但是我們要通過對偶問題來求解原始問題，就必須使得原始問題的最優值與對偶問題的最優值相等，於是可以得出下麵的推論：
推論：設
分別是原始問題和對偶問題的可行解，如果
，那麼
所以，當原始問題和對偶問題的最優值相等：時，可以用求解對偶問題來求解原始問題（當然是對偶問題求解比直接求解原始問題簡單的情況下），但是到底滿足什麼樣的條件才能使的呢，這就是下麵要闡述的 KKT 條件
4. KKT 條件
定理：對於原始問題和對偶問題，假設函數
是凸函數，
是仿射函數（即由一階多項式構成的函數，f(x)=Ax + b, A是矩陣，x，b是向量）；並且假設不等式約束
有
，則存在
是原始問題的最優解，
是對偶問題的最優解，並且
定理：對於原始問題和對偶問題，假設函數
關於KKT 條件的理解：前面三個條件是由解析函數的知識，對於各個變數的偏導數為0（這就解釋了一開始為什麼假設三個函數連續可微，如果不連續可微的話，這裡的偏導數存不存在就不能保證），後面四個條件就是原始問題的約束條件以及拉格朗日乘子需要滿足的約束。
特別註意當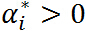
時，由KKT對偶互補條件可知：
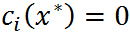，這個知識點會在 SVM 的推導中用到.
5. 總結
一句話，某些條件下，把原始的約束問題通過拉格朗日函數轉化為無約束問題，如果原始問題求解棘手，在滿足KKT的條件下用求解對偶問題來代替求解原始問題，使得問題求解更加容易。
