INTRODUCTION：

首先，什麼是割點？

在一個有N個節點，M條邊的有向圖中，若刪去一個點，以及所有與這個節點直接相連的邊，會使該圖不連通、或出現更多互不連通的子圖（原圖本身就不連通的情況），則稱這個點為割點。

那麼不難想到割點的一種求法：

一、暴力枚舉：

枚舉每一個節點，判斷該節點是否是割點（沒有什麼是暴力解決不了的）

不過顯然暴力枚舉太慢了，出題人也不想讓你這麼輕鬆就AC

因此，可以用以下兩種方法快速的求出割點：

二、DFS樹：

首先來設想一下，假如我們用DFS來遍歷一張無向圖連通圖，保證每個點只被遍歷到一次，然後將遍歷時經過的每一個點，每一條邊取出，組成一個新的聯通圖，顯而易見：這張新圖必然是一棵樹。

我們稱這棵樹為DFS樹，同時不難看出，由於遍歷時所選的根節點不同，遍歷的順序不同，所以這顆DFS樹並不唯一，不過這對於求割點而言影響不大，所以只要任意求出一顆DFS樹就可以了

對於原圖而言，我們將構成DFS樹的邊稱為樹邊，不屬於DFS樹的邊稱為非樹邊

存在一個結論：對於每一條非樹邊，他只可能連接DFS樹上某個節點和他的祖先，不可能連接兩個分別位於不同子樹上的節點，我們稱這樣連接DFS樹上的某個節點與他的祖先的非樹邊為返祖邊。

如圖所示，只存在形如邊I的返祖邊，不存在形如邊J的橫跨邊

圖1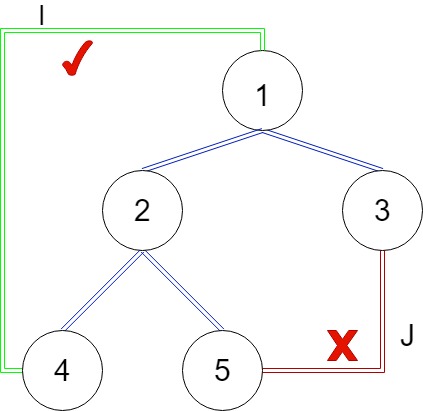證明：若存在邊J，則在DFS時必然會先經過邊J由5節點遍歷到3節點，形成如下圖形，不可能會形成一條橫跨邊。

圖2：藉助DFS樹的這些性質，我們就可以求割點了：

分三種情況討論:

1.若該節點是葉子節點，那麼他一定不是割點

2.若該節點是根節點，那麼若他的子樹數量大於等於2，則他是割點，若他只有一顆子樹，則他不是割點

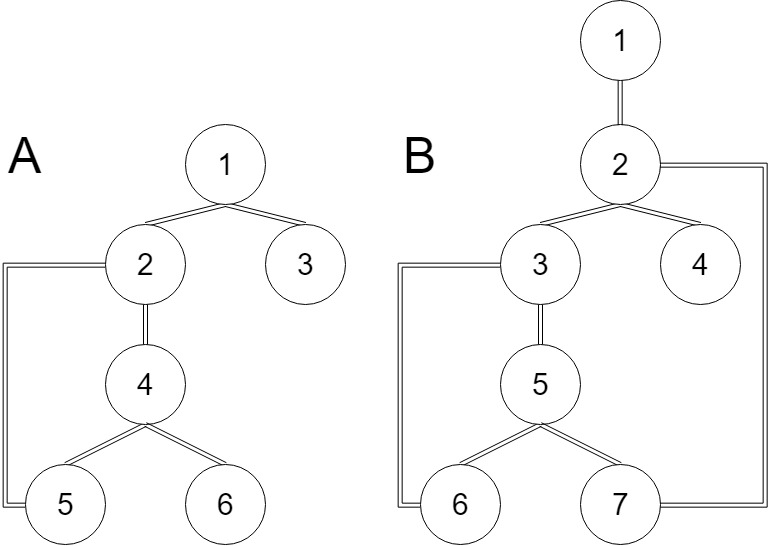
3.若該節點既不是根節點也不是葉子節點，則若他的每一顆子樹都中存在一條返祖到他的祖先節點（不包括）的返祖邊，則他不是割點（如上圖2中的2、5節點）反之他是割點

如圖所示：圖A中的1節點是一個割點，4節點是一個割點，圖B中的1節點不是一個割點，5節點不是一個割點

代碼如下：

  1 #include<cstdio>
  2 #include<cstring>
  3 #include<iostream>
  4 #include<algorithm>
  5 using namespace std;
  6 const int maxn = 100010;
  7 const int maxm = 500005;
  8 int n, m;
  9 int tot, ans;
 10 bool vis[maxn];
 11 struct edge
 12 {
 13     int to;
 14     int next;
 15     bool t;//這條邊是否是一條從子節點到父節點的邊
 16     bool flag;//是否是樹邊
 17 }e[maxm];
 18 struct node
 19 {
 20     int f;//該節點的父節點
 21     int to;//該節點及其子樹的所有節點的返祖邊能夠到達的最淺深度
 22     int son;//該節點的子節點的個數
 23     int deep;//該節點的深度
 24     int head;
 25     bool root;//是否是根節點
 26     bool flag;//是否是割點
 27 }p[maxn];
 28 void add(int u, int v)
 29 {
 30     tot++;
 31     e[tot].to = v;
 32     e[tot].next = p[u].head;
 33     p[u].head = tot;
 34 }
 35 void dfs(int u, int f)//u代表當前節點,f代表該節點的父節點
 36 {
 37     vis[u] = 1;
 38     p[u].deep = p[f].deep + 1;//記錄深度
 39     p[u].to = p[u].deep;//初始設該節點及其子樹所能夠連接的最淺深度為該節點的深度
 40     for (int i = p[u].head; i; i = e[i].next)//枚舉該節點的所有子節點
 41     {
 42         int v = e[i].to;
 43         if (!vis[v])
 44         {
 45             p[u].son++;//記錄子節點的數量
 46             p[v].f = u;//記錄u的子節點的父節點為u
 47             e[i].flag = 1;//這條邊屬於樹邊
 48             dfs(v, u);
 49         }
 50     }
 51 }
 52 void init(int u)//處理每個節點的子樹
 53 {
 54     for (int i = p[u].head; i; i = e[i].next)//更新每一個節點的子樹所能抵達的最淺深度
 55     {
 56         int v = e[i].to;
 57         if (e[i].flag && !e[i].t)
 58         {
 59             init(v);
 60             p[u].to = min(p[u].to, p[v].to);
 61         }
 62     }
 63 }
 64 bool check(int u)
 65 {
 66     for (int i = p[u].head; i; i = e[i].next)
 67     {
 68         if (e[i].flag && !e[i].t)
 69         {
 70             int v = e[i].to;
 71             if (!(p[v].to < p[u].deep))
 72                 return 0;
 73         }
 74     }
 75     return 1;
 76 }
 77 void work()//判斷每一個節點是否是割點
 78 {
 79     for (int u = 1; u <= n; u++)
 80     {
 81         if (u == 1)//u是根節點
 82         {
 83             if (p[u].son <= 1)
 84                 p[u].flag = 1;//不是割點
 85         }
 86         else if (p[u].son == 0)
 87             p[u].flag = 1;
 88         else
 89         {
 90             if (check(u))
 91                 p[u].flag = 1;
 92         }
 93     }
 94 }
 95 int main()
 96 {
 97     cin >> n >> m;
 98     for (int i = 1; i <= m; i++)
 99     {
100         int u, v;
101         cin >> u >> v;
102         add(u, v);
103         add(v, u);
104     }
105     dfs(1, 0);
106     //處理最小深度
107     //註意要特判從兒子節點到父節點的邊（樹邊的一半），否則所有節點（都被認為可以到達根節點）
108     for (int u = 1; u <= n; u++)
109     {
110         for (int i = p[u].head; i; i = e[i].next)
111         {
112             int v = e[i].to;
113             if (!e[i].flag && v != p[u].f)//若這條邊是樹邊且不是由兒子節點到父節點
114             {
115                 p[u].to = min(p[u].to, p[v].deep);//更新u能抵達的最前深度
116             }
117             if (v == p[u].f)
118                 e[i].t = 1;
119         }
120     }
121     init(1);
122     work();
123     for (int i = 1; i <= n; i++)
124         if (!p[i].flag)
125             ans++;
126     cout << ans << endl;
127     for (int i = 1; i <= n; i++)
128         if (!p[i].flag)
129             cout << i << " ";
130     return 0;
131 }

不過上面的代碼只能處理原圖聯通的情況，如果原圖不連通則需要多跑幾次（看成多個不同的連通圖）

三、tarjan：

可以看出：以上用DFS樹求割點的演算法相當繁瑣，相比之下，tarjan可以更加簡單快捷的求出割點（並且不需要特判圖的連通性）

分兩種情況討論：

1.對於根節點：若該節點的子節點的數量大於等於2則該節點是割點

2.對於其他節點：設該節點為u，設該節點的子節點為v，若存在low[v]>=dfn[u]則節點u為割點（類比DFS樹第二種情況）

代碼如下：

 1 #include<stack>
 2 #include<vector>
 3 #include<string.h>
 4 #include<iostream>
 5 #include<algorithm>
 6 using namespace std;
 7 const int maxn = 100010;
 8 int ans;
 9 int n, m, id;
10 int dfn[maxn];
11 int low[maxn];
12 bool flag[maxn];//記錄每一個點是否是割點
13 vector<int> e[maxn];//vector存圖
14 void tarjan(int u, int f)//普通的tarjan
15 {
16     int child = 0;//記錄該節點有幾個子節點
17     low[u] = dfn[u] = ++id;
18     for (int i = 0; i < e[u].size(); i++)
19     {
20         int v = e[u][i];
21         if (!dfn[v])
22         {
23             tarjan(v, f);
24             low[u] = min(low[u], low[v]);
25             if (low[v] >= dfn[u] && u != f)
26                 flag[u] = 1;
27             if (u == f)
28                 child++;
29         }
30         low[u] = min(low[u], dfn[v]);
31     }
32     if (child >= 2 && u == f)
33         flag[u] = 1;
34 }
35 int main()
36 {
37     cin >> n >> m;
38     for (int i = 1; i <= m; i++)
39     {
40         int u, v;
41         cin >> u >> v;
42         e[u].push_back(v);
43         e[v].push_back(u);
44     }
45     for (int i = 1; i <= n; i++)//原圖不一定聯通，所以只要節點i尚未被遍歷過
46         if (!dfn[i])//就要以i為根節點運行一次tarjan
47             tarjan(i, i);
48     for (int i = 1; i <= n; i++)
49         if (flag[i])
50             ans++;
51     cout << ans << endl;
52     for (int i = 1; i <= n; i++)
53         if (flag[i])
54             cout << i << " ";
55     return 0;
56 }

 --會寧狐狸