canvas教程(三) 繪製曲線

經過 canvas 教程(二) 繪製直線 我們知道了 canvas 的直線是怎麼繪製的

而本次是給大家帶來曲線相關的繪製

繪製圓形

在 canvas 中我們可以使用 arc 方法畫一個圓

context.beginPath();
context.arc(x, y, r, startRadian, endRadian, antclockwise);
context.closePath();

我們是第一次用到 beginPath 和 closePath 這兩個方法，首先這兩個方法故名思意就是開始路徑和結束路徑，一般都是配合使用的。

對於 arc 的方法的參數，x 和 y 代表的是圓心的坐標，r 是指圓的半徑，startRadian 和 endRadian 是指開始的角度和結束的角度

註意：這裡是以弧度為單位的！

1π 等於 180 度，所以我們這裡寫的時候一般是寫成 度數*Math.PI/180，方便我們一眼看出度數是多少

而 antclockwise 是指是否是逆時針繪製，預設是 false

有朋友會說了，我試了一下，寫了這三句沒有效果啊，怎麼回事？沒有效果是肯定的，因為這三句僅僅只是描述了一個路徑！並沒有繪製！所以我們可以用上繪製直線中使用的“描邊”stroke 或者“填充”fill

描邊三角形：

context.beginPath();
context.arc(x, y, r, startRadian, endRadian, antclockwise);
context.closePath();
context.strokeStyle = '顏色值';
context.stroke();
//描邊 填充fill 同理  就不寫了

繪製弧線

弧線是圓的一部分，那麼如何繪製一個弧度呢，有朋友就發現了我們剛纔的 arc 也有一個弧度，
只是兩個弧度之間的點有連接的一條直線，那麼我去掉直線是不是就是弧線了呢？賓果！就是這樣，只要你去掉 closePath 就會發現你畫了一條弧線了 2333

好了那麼 canvas 其實還有一個畫弧線的方法 arcTo(x1,y1,x2,y2,radius);

我們要通過 arcTo 畫一條弧線，需要提供三個點的坐標，開始點一般是通過 moveTo 和 lineTo 提供
x1 和 y1 是控制點，x2 和 y2 是結束點，radius 則是圓弧的半徑

arcTo()方法將利用當前端點、端點 1(x1,y1)和端點 2(x2,y2)這三個點所形成的夾角

然後繪製一段與夾角的兩邊相切並且半徑為 radius 的圓上的弧線

弧線的起點就是當前端點所在邊與圓的切點

弧線的終點就是端點 2(x2,y2)所在邊與圓的切點，並且繪製的弧線是兩個切點之間長度最短的那個圓弧。

如果當前端點不是弧線起點，arcTo()方法還將添加一條當前端點到弧線起點的直線線段。

我畫一個圖：

咳咳，別介意畫工，大概就是這樣的，開始點是我們的當前的點就是使用 arcTo 之前的點
下麵我寫兩段代碼演示一下起點一致和起點不一致的情況

    context.moveTo(50, 50);
    context.lineTo(150, 50);
    ctx.arcTo(200,50, 200,100, 50);
    ctx.stroke();

    context.moveTo(50, 50);
    ctx.arcTo(200,50, 200,100, 50);
    ctx.stroke();

是不是發現結果是一樣的！

其中區別就細細品味吧，數學知識可以補一補

繪製貝塞爾曲線

百度百科：貝塞爾曲線(Bézier curve)，又稱貝茲曲線或貝濟埃曲線，是應用於二維圖形應用程式的數學曲線。一般的矢量圖形軟體通過它來精確畫出曲線，貝茲曲線由線段與節點組成，節點是可拖動的支點，線段像可伸縮的皮筋，我們在繪圖工具上看到的鋼筆工具就是來做這種矢量曲線的。貝塞爾曲線是電腦圖形學中相當重要的參數曲線，在一些比較成熟的點陣圖軟體中也有貝塞爾曲線工具，如PhotoShop等。

更多的就大家自行搜索吧，由於一次貝塞爾曲線就是直線，這裡就不講了，我們直接講 canvas 如何繪製二次貝塞爾曲線

二次貝塞爾曲線

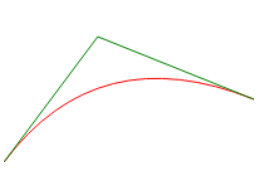
cnavas 提供了一個方法 quadraticCurveTo(x1,y1,x2,y2)， 其中參數 x1 和 y1 是控制點，x2 和 y2 是結束點

起始點是調用方法之前的點

動圖我不會畫，但是我之前網上找到一個:

context.strokeStyle = 'red';
context.beginPath();
context.moveTo(0, 150);
context.quadraticCurveTo(75, 50, 200, 100);
context.stroke();
context.strokeStyle = 'green';
context.beginPath();
context.moveTo(75, 50);
context.lineTo(0, 150);
context.moveTo(75, 50);
context.lineTo(200, 100);
context.stroke();

代碼效果:

三次貝塞爾曲線

三次貝塞爾曲線的方法則是 bezierCurveTo(x1,y1,x2,y2,x3,y3)

其中參數 x1、y1，x2、y2 是控制點，x3 和 y3 是結束點
就是提供多一個控制點！

畫圖原理是這樣:

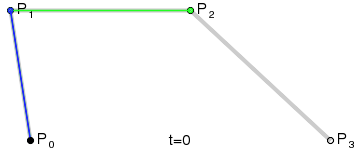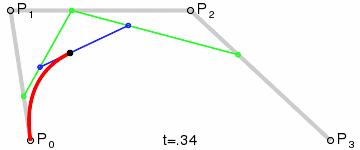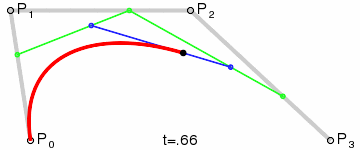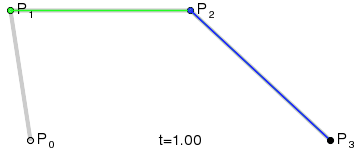
這個例子就不寫了，大家照著二次貝塞爾曲線的例子，練習一下！

結束

本次講了：繪製圓形、繪製弧線、二次貝賽爾曲線、三次貝賽爾曲線，大家學會了多少呢？

好了，本次的教程就到這裡結束了，下次將為大家帶來線條和文本的操作