生成前N個自然數隨機置換的3個程式

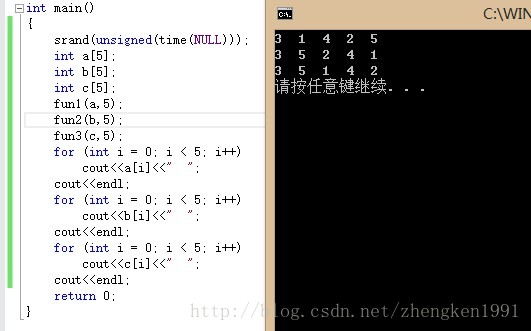
問題描述：

假設需要生成前N個自然數的一個隨機置換。例如，{4，3，1，5，2}和{3，1，4，2，5}就是合法的置換，但{5，4，1，2，1}卻不是，因為數1出現兩次而數3卻沒有。這個程式常常用於模擬一些演算法。我們假設存在一個隨機數生成器RandInt(i,j)，它以相同的概率生成i和j之間的一個整數。

int RandInt(int i, int j)       //srand()放在主函數中了
{
    if(i==0)
        return rand()%(j+1);
    else
        return rand()%(j-i+1) + i;
}

演算法一： 時間複雜度O（N²logN）

填入從a[0]到a[n-1]的數組a,為了填入a[i]，生成隨機數直到它不同於已經生成的a[0],a[1],...,a[i-1]時，再將其填入a[i].

void fun1(int a[], int n)
{
    int tmp;
    for (int i = 0; i < n; i++)
    {
        tmp=RandInt(1, n);
        for (int j = 0; j < i; j++)
        {
            if(tmp==a[j])
            {
                tmp=RandInt(1, n);
                j=-1;
            }
        }
        a[i] = tmp;
    }
}

演算法二：時間複雜度O(NlogN)

同演算法一，但要保存一個附加的數組，稱之為Used(用過的)數組。當一個隨機數ran最初被放入數組A的時候，置Used[ran]=1。

void fun2(int a[], int n)
{
    int tmp;
    for (int i = 0; i < n; i++)
    {
        tmp=RandInt(1, n);
        while(used[tmp]!=0)
            tmp=RandInt(1, n);
        a[i]=tmp;
        used[tmp]=1;
    }
}

演算法三：時間複雜度O(N)

填寫該數組使得a[i]=i+1.然後：

for(i=1; i<N; i++)
swap(&a[i], a[RandInt(0,i)]);

void swap(int &a, int &b)
{
    int tmp=a;
    a=b;
    b=tmp;
}
 
void fun3(int a[], int n)
{
    for (int i = 0; i < n; i++)
    {
        a[i]=i+1;
    }
    for (int i = 1; i < n; i++)
    {
        swap(a[i], a[ RandInt(0, i) ]);
    }
}

運行效果：