leadcode的Hot100系列--78. 子集--回溯

上一篇說了使用位運算來進行子集輸出，這裡使用回溯的方法來進行排序。
回溯的思想，我的理解就是：

把解的所有情況轉換為樹或者圖，然後用深度優先的原則來對所有的情況進行遍歷解析。

當然，因為問題中會包涵這各種各樣的限制條件，我們可以用這些限制條件去減少遍歷的分支。
其實，比較著名的就是0-1背包問題，這個背包問題之後再說，這裡先看排列組合。

假設我們的數組為[6,7,8]，依然使用0來表示當前數字不存在，用1來表示當前數字存在，我們就可以畫出這樣一個樹：

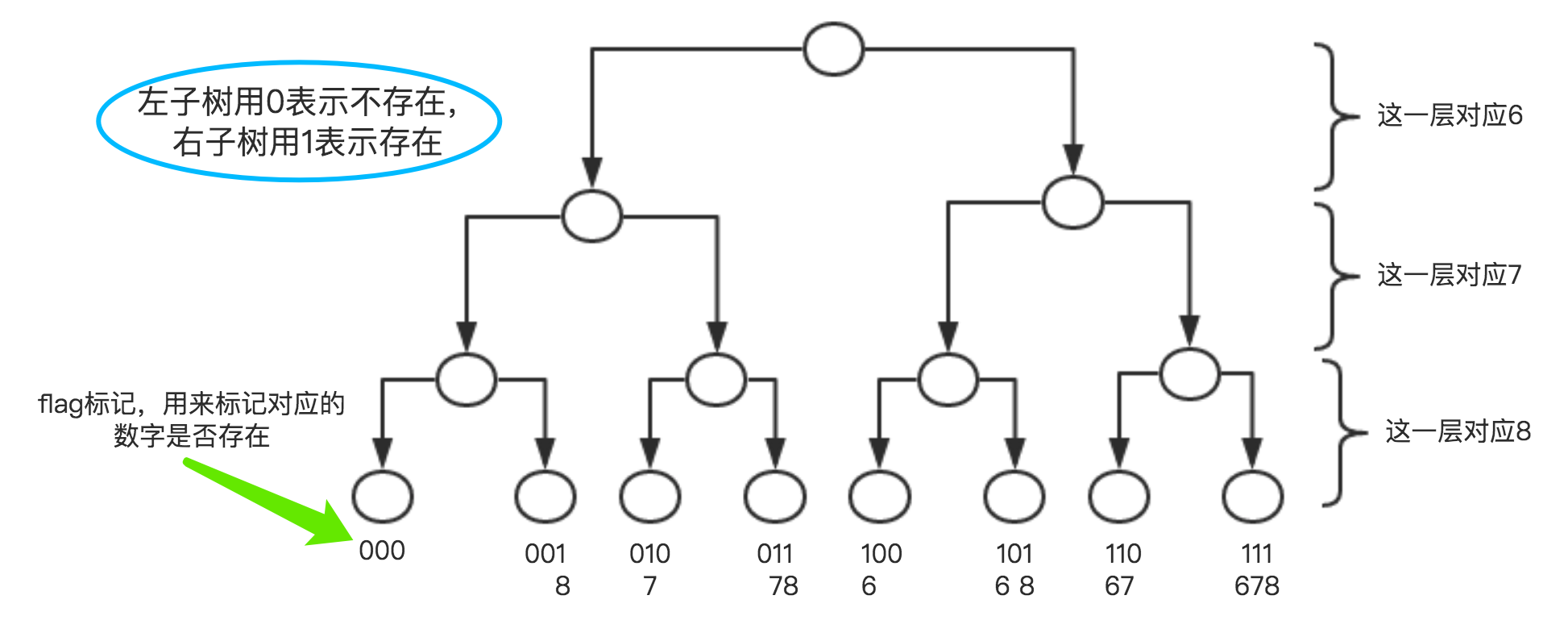
這裡使用遞歸來生成對應的flag標記，重點是backtrack函數:

#include <stdio.h>

int x[] = {6,7,8};   // 需要排列的數組
int y[] = {0,0,0};   // 存放flag標記
int level = 3;       // 有3個數字需要進行排列，對應的就需要排3層

void show()
{
    for (int i=0; i<level; i++)
    {
        printf("flag : %d ", y[i]);
    }
    printf("\n");
}

void backtrack (int t)
{
    if (t == level)   // 當遍歷深度等於level的時候，說明遍歷完成，得到一組完整的flag標記
        show();
    else  
        for (int i=0;i<=1;i++)   // 這裡先生成0標記，再生成1標記
        {
            y[t]=i;            //  記錄當前層是否存在，0存在，1不存在
            backtrack(t+1);   // 遞歸遍歷下一層，這裡可以根據題目限制來判斷是否需要繼續下一層的遍歷，可以減少遍歷次數
        }
}

int main(void)
{
    backtrack(0);
    return 0;
}

輸出結果為：
0 0 0 
0 0 1 
0 1 0 
0 1 1 
1 0 0 
1 0 1 
1 1 0 
1 1 1 

回溯的基本就那麼一個思想，那限制條件怎麼用呢？
比如，我有10元錢，這裡有三個物品，價格分別是8元，5元，2元，10元，
問，這10元錢可以有哪些買法？
這裡存在的一個限制就是：總數不能超過10。

#include <stdio.h>

#define TOTAL 10  // 總數最多為10

int x[] = {8,5,2,10};  // 價格
int y[] = {0,0,0,0};
int level = 4;

void show()
{
    int n=0;
    for (int i=0; i<level; i++)   // 計算總價格是否超過10
    {
        n += y[i] * x[i];
    }
    if (TOTAL < n)
    {
        return;
    }
    for (int i=0; i<level; i++)   // 這裡直接列印符合條件的價格
    {
        printf("%d ", y[i]*x[i]);
    }
    printf("\n");
}

void backtrack (int t)
{
    if (t == level)
        show();
    else  
        for (int i=0;i<=1;i++) 
        {
            y[t]=i;
            int n = 0;
            for (int j=0; j<t; j++)  // 這裡先計算一下當前價格是多少
            {
                n = y[j] * x[j];
            }
            if (TOTAL > n)       // 如果當前價格已經超了，就不需要再遞歸下一層(因為不論下一層是否存在，總價格必然會超)，否則繼續遞歸
                backtrack(t+1);
        }
}

int main()
{
    backtrack(0);
    return 0;
}
結果為：
0 0 0 0 
0 0 0 10 
0 0 2 0 
0 5 0 0 
0 5 2 0 
8 0 0 0 
8 0 2 0