前言:由於對面向對象思想認識的不夠深刻,所以這一單元的作業寫的是非常不oo的,從代碼結構來看,結構也顯得有些混亂,,沒有一個清晰的設計。 作業分析 第一次作業 反思 1. 輸入 對於三次的作業其實大部分的難點就是在判斷輸入的合法性上,對於第一次作用來說,最初的想法還是用一整個正則表達式來判斷輸入,但 ...
前言:由於對面向對象思想認識的不夠深刻,所以這一單元的作業寫的是非常不oo的,從代碼結構來看,結構也顯得有些混亂,,沒有一個清晰的設計。
作業分析
第一次作業
反思
- 輸入
對於三次的作業其實大部分的難點就是在判斷輸入的合法性上,對於第一次作用來說,最初的想法還是用一整個正則表達式來判斷輸入,但是這樣就會出現爆棧的問題,所以轉換思路去匹配每一項,其實對於三次作業我認為正確的判斷輸入的做法應該是不斷的劃分到底層在進行正則的合法性的判斷,也能夠使程式有一定的擴展性,對於第一次來說,可以把項在劃分為因數,由於第一次經驗的缺少和作業需求的相對簡單,所以只在項的層面進行了判斷,這就造成了正則形式過於複雜,同時我個人採取的劃分表達式的方法是尋找\d[+-]和x[+-],這種方法無疑是只能針對本次作業有效,缺乏擴展性。 - 優化
對於這次的優化,思路也很清楚,就是把相同冪次的繫數合併,採用hashmap來存儲數據,但是沒有在hashmap里使用自定義的類。
出現的bug
由於第一次作業相對簡單,所以即便是非常粗糙的代碼結構也沒有出現很多bug,其中一個bug是因為優化0不輸出,所以會出現輸出為空的情況,針對這種情況,我才用了輸出時進行特判來避免。
代碼度量
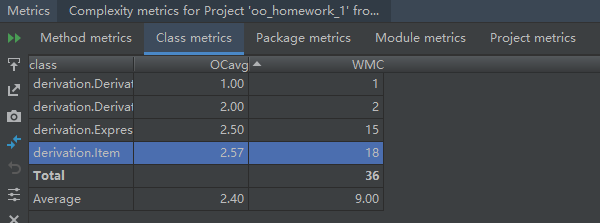
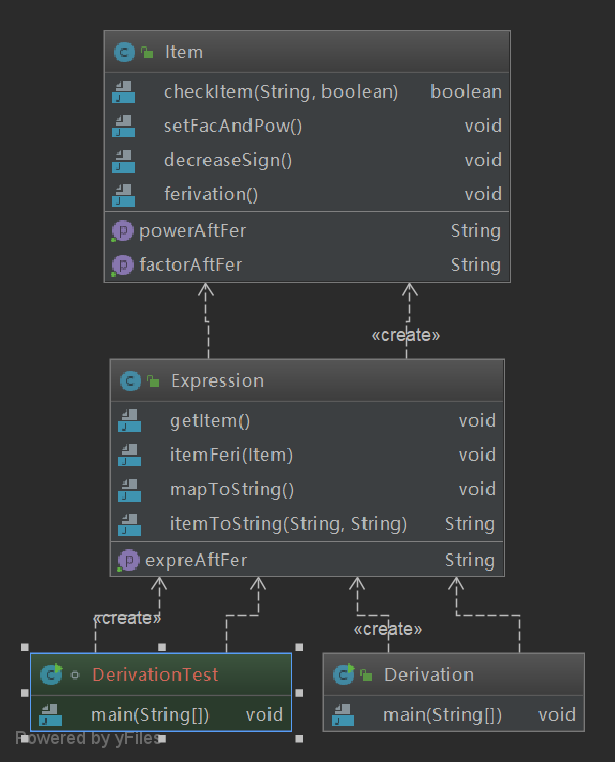
從對輸出的處理可以看到,整體代碼分為了三個class,分別處理表達式,項,和主函數,整體結構還算清晰。
但是這種處理方法卻對第二次作業帶來了災難。
第二次作業
反思
- 輸入
第二次的作業,在第一次的基礎上增加了sin(x)和cos(x),但本質上還是相乘,所以仍採用了第一次的方法,劃分為項然後判斷合法性,但是這次項的情況更為複雜,所以項的正則就變得異常複雜,而且難以看懂,同時這種正則也帶來了很多bug。 - 求導
由於這次的作業已經不是簡簡單單的對冪函數求導,所以應用函數求導的法則之後,一個項求導後會變成三個項的和,所以無奈在項的裡面加了一個數組來存這三個求導之後的項,並且求導之前的合併繫數也變得很麻煩。 - 優化
這次採用了把自定義的類作為hashmap的鍵,但是由於很菜,並沒有對三角函數進行優化。
出現的bug
由於這次沒有把item劃分為factor,所以導致判斷item的正則很複雜,結構對item的判斷出現了很多bug,例如sin(x)*,筆者在改bug的時候甚至看不懂原來寫的正則。。。
代碼度量
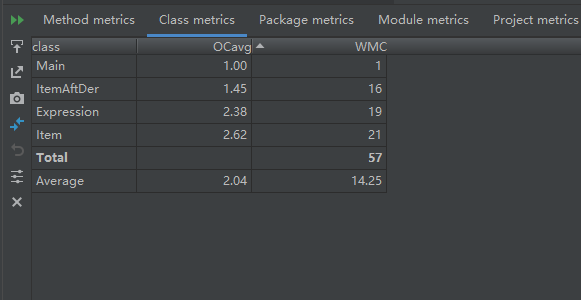
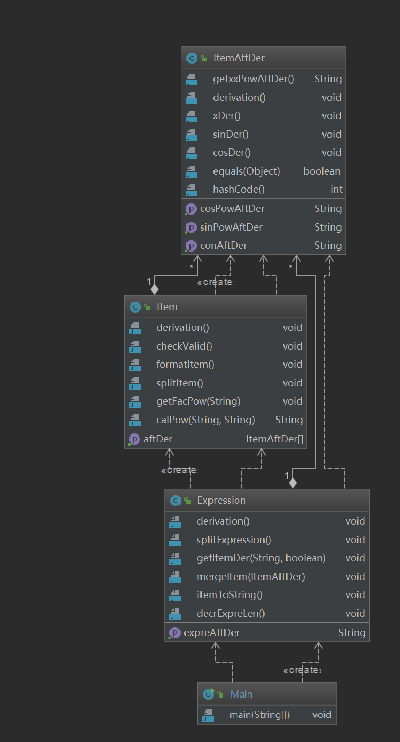
第三次作業
反思
- 輸入
這次的作業難度提升幅度巨大,所以之前的方法已經徹底不能再使用,所以經過思考之後,採用樹狀的形式來儲存數據。
- 首先按照加減把表達式分割為項(註意分割時判斷加減號是否在一對括弧里,以及加減號之前是否有乘號)
- 在按照乘號把項分割為因數(同樣需要註意乘號是否在一對括弧里)
- 得到的因數如果是被一對括弧包圍,則是一個表達式因數,繼續從1開始判斷,否則為基礎的常數因數,冪函數,三角函數。
2.求導
因為是採用了樹狀的結構,所以在求導時也同樣在樹上求導,使得整個過程變得簡化。
3.優化
這次的優化就只做了減少括弧,對於0,1的不輸出。
出現的bug
這次的bug是對可能出現情況考慮的不周全,例如sin(-2)是一個合法的輸入,而sin(- 2)就不是一個合法的輸入,對於sin內部是否一個因數考慮的不夠周全。
代碼度量
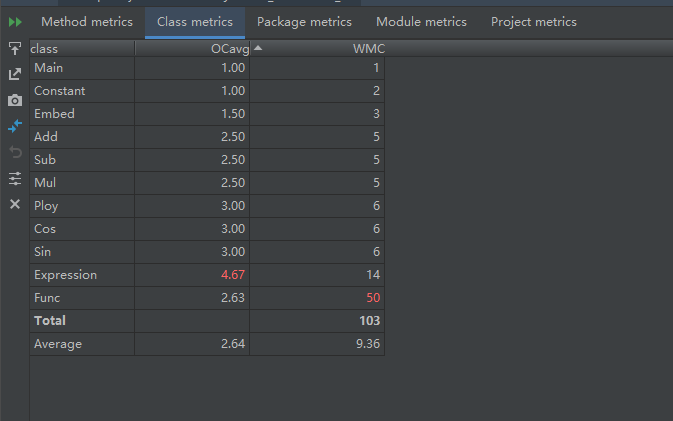
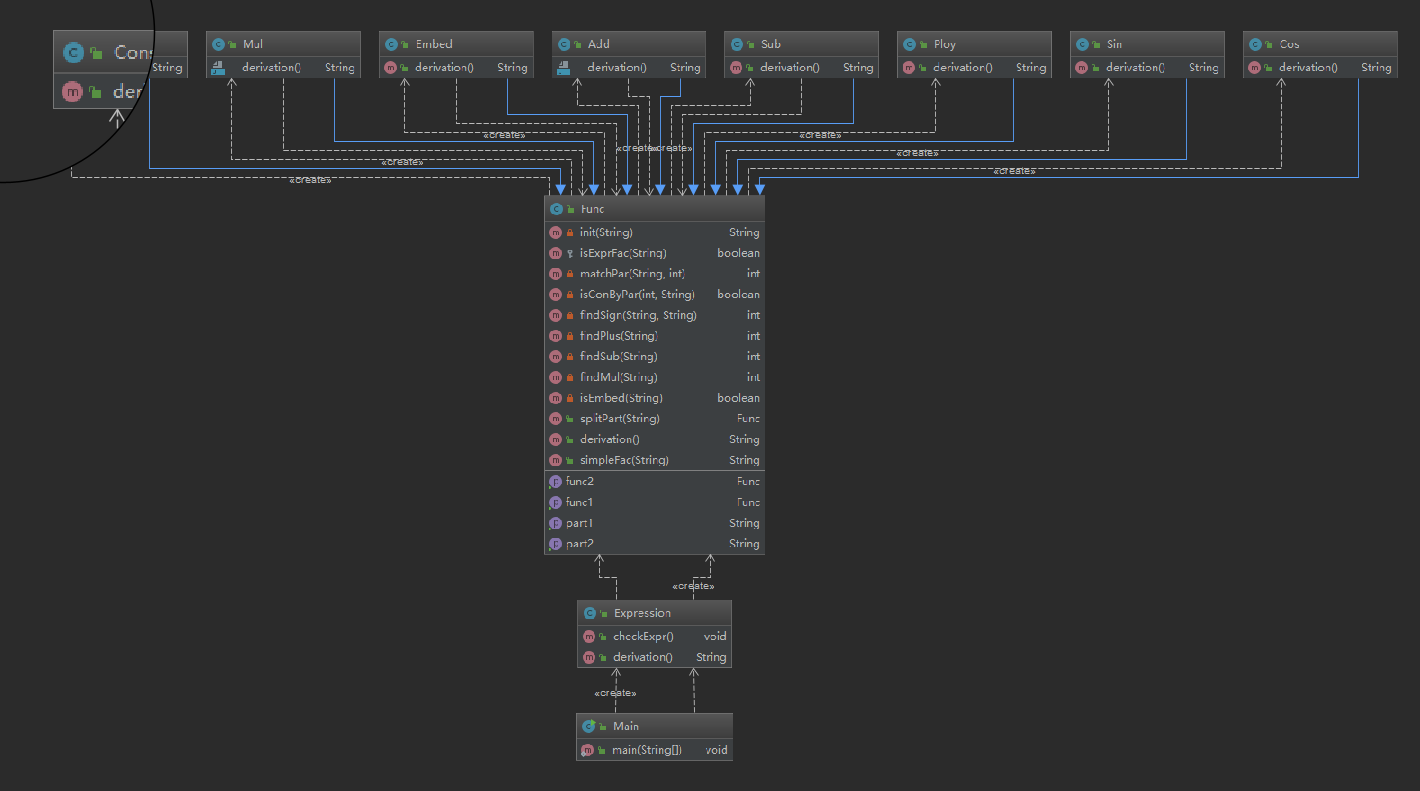
通過類圖可以看到,在這次作業中,按照指導書的提示,把整個表達式分為加法,乘法,嵌套,各種基礎函數,構成樹的形式,其中,6種函數都是func的子類,通過轉型的機制,可以在父類中共用字串分割,在子類中重寫各自的求導方法,並且這個方法有一定的擴展性。
尋找自己程式的bug
主要通過對作業要求的理解,通過腳本生成一些測試,但是當程式的大體邏輯沒有問題時,這種方法往往覆蓋不到一些特殊點,所以還會手寫一些測試數據,但是這些根本上還是依賴於對作業要求理解的完整性。所以與同學交流測試數據也很重要。
發現別人的bug
主要的策略還是讀別人的代碼,這可能也是互測的根本意義所在,在讀別人代碼時,也會先用一些自認為特殊的數據先試一試,然後大體過一遍他的邏輯,因為這三次作業,其實大家的處理思路不是一模一樣,但有很多的相似之處,所以對與自己處理有很大出入的地方會著重看。
這幾周以來的oo的感想
雖然oo非常的緊張刺激,其中可能有很幸運沒有被強測找到bug,也會有互測被刀了很多次,也可能有強測直接爆炸,但是最重要的是我們從中學到了東西,如果我們做的不夠好,不管這是不是最有效的訓練方法,只能說明我們的能力還有很大的不足,就學到東西就好了。



